1. 误差
Error的来源
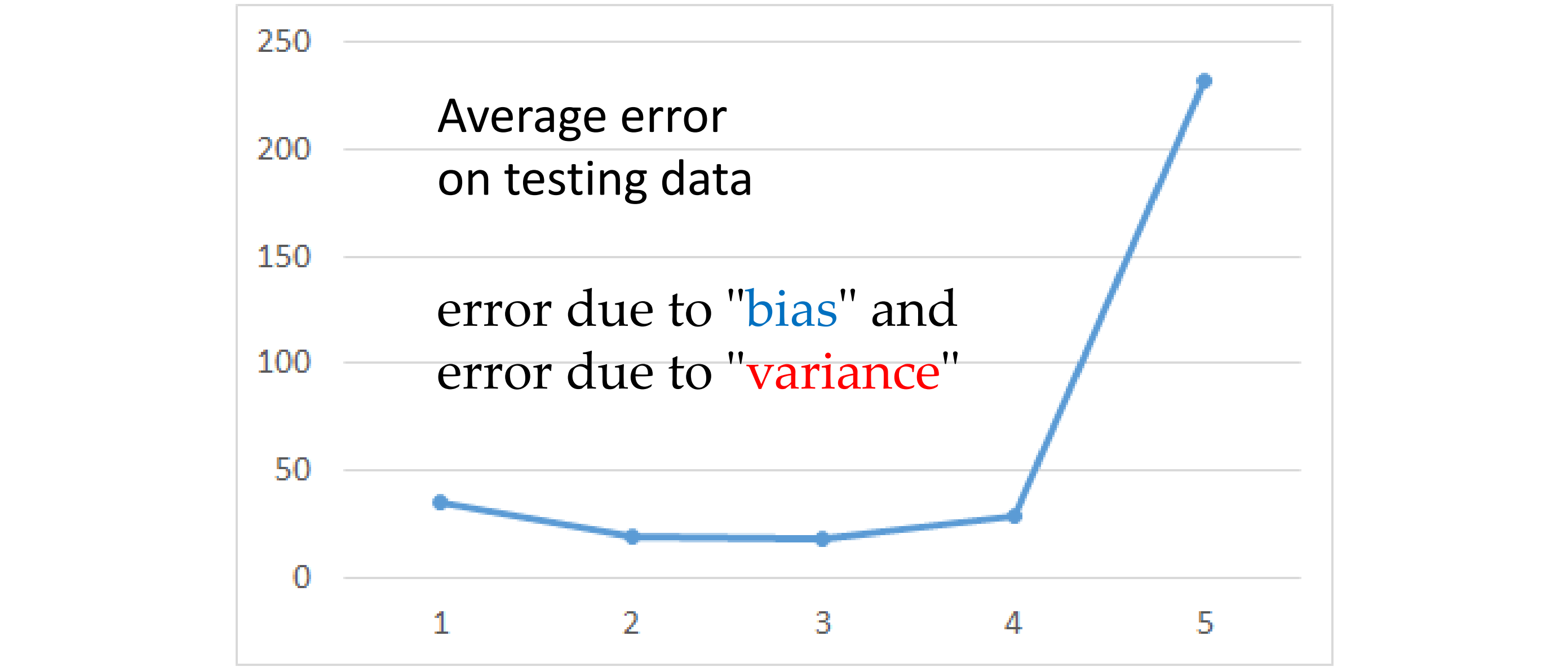
根据上节课测试集数据得到,Average\ ErrorAverage Error 随模型复杂增加呈指数上升趋势。更复杂的模型并不能给测试集带来更好的效果,而Error的主要有两个来源,分别是bias和variance。
Bias、Variance和Erroe的关系可参考 机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系?
估测
假设真实的模型(理论最佳)为, 如果我们知道
模型,那是最好不过了,但
只有 Niamtic 公司(宝可梦开发公司)才知。

所以我们只能通过收集Pokemon精灵数据,然后通过 step1~step3 训练得到我们的理想模型c,其实是
的一个预估值。

这个过程就像打靶,是靶心,
就是我们投掷的结果。如上图所示,
与
之间蓝色部分的差距就是偏差(bias)和方差(variance)导致的。
估测变量x的偏差和方差
首先理解偏差和方差怎样计算: 偏差(Bias)和方差(Variance)——机器学习中的模型选择
- 假设x的平均值是
,方差是
,如何评估平均值呢?
- 首先,拿到N个样本点,
- 计算平均值m,得到
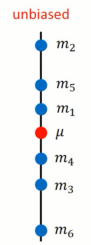
计算多组,
期望:
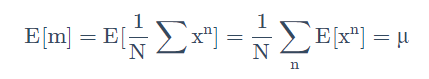
这便是无偏估计。
分布对于
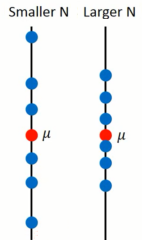
的离散程度(方差):

N越小越离散(越不准):

为什么有很多模型
假设在平行宇宙中,抓到不同的神奇宝贝:
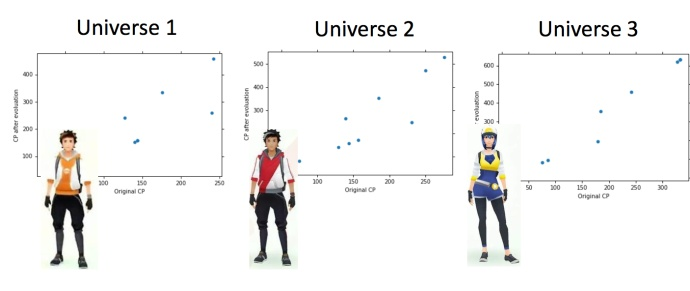
同一个model,在不同的训练数据集中找到的不一样:
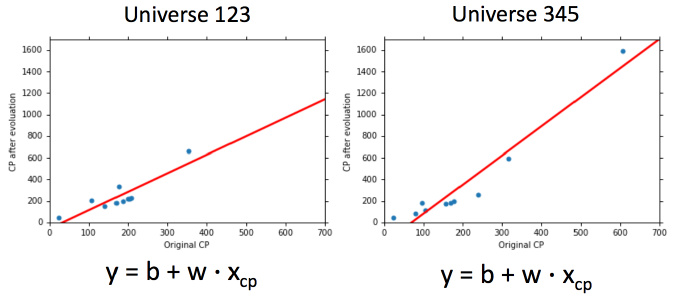
就像在靶心上射击,进行了很多组(一组多次)。现在需要知道它的散布是怎样的,将100个宇宙中的model(100个不同的w和b)画出来如图:
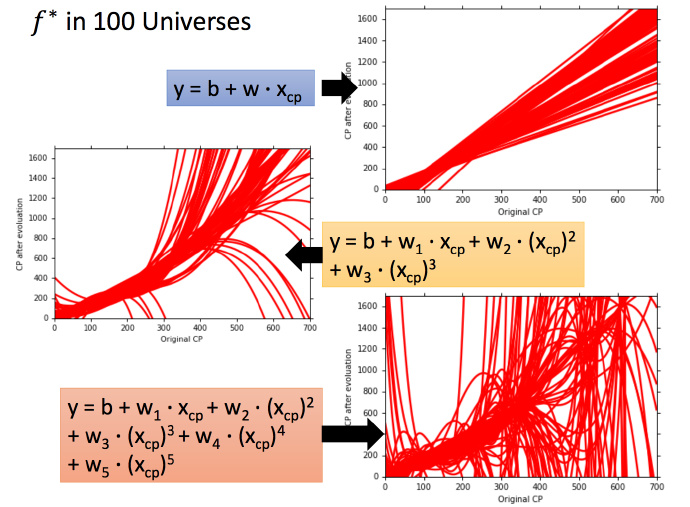
一次模型的方差较小,也就是比较集中,离散程度较小。而5次模型的方差就比较大,同理散布比较广,离散程度较大。
通常简单的模型,方差较小(就像每次射击结果都集中在一个比较小的区域内)。复杂模型,方差较大大,散布比较开。
这是因为简单的模型受到不同训练集的影响较小。

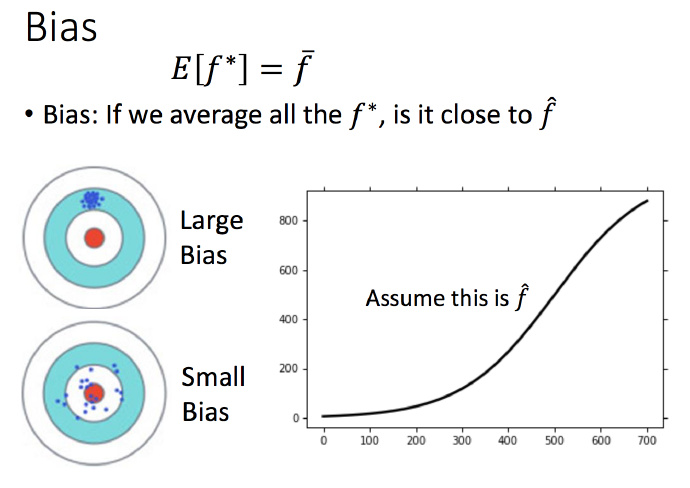
由于无法知道真正的 ,假设图中黑色曲线为真正的
结果显示,1次平均的没有5次的好,5次模型离散程度很高。
1次模型的偏差比较大,复杂的5次模型,偏差较小。
直观解释:简单模型函数集的space较小,所以可能space中没有包含靶心,肯定射不中。而复杂的模型函数集的space较大,可能包含靶心,只是没有办法找到确切的靶心在哪,但足够多的,就可能得到真正的。
偏差(bias)与方差(variance)

将误差拆分为偏差和方差。简单模型(左边)是偏差较大造成的误差,叫做欠拟合,复杂模型(右边)是方差过大造成的误差,叫做过拟合。
如何判断误差来源
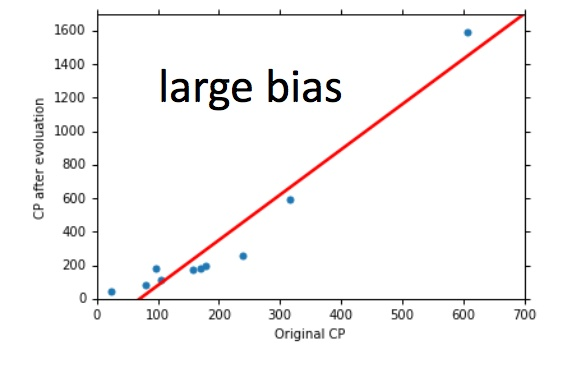
如果模型没有很好的训练集,就是偏差过大,欠拟合;如果模型很好的训练集,即在训练集上得到很小的错误,但在测试集上得到大的错误,这意味着模型可能是方差比较大,就是过拟合。 对于欠拟合和过拟合,分别对应不同的处理方法。
考虑重新设计模型。因为之前的函数集里面可能根本没有包含。可以:
- 将更多的函数加进去,比如考虑高度重量,或者HP值等等。
- 考虑更多次幂、更复杂的模型。
- 如果此时强行再收集更多的data去训练,没有什么帮助,因为设计的函数集本身不够好,再找更多的训练集作用不大。
- 寻找更多数据
- Regularization
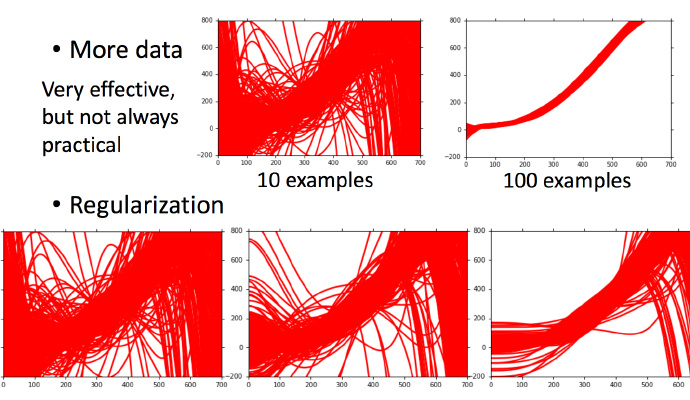
但是很多时候不一定能做到收集更多的data。可以针对对问题的理解对数据集做调整。比如识别手写数字的时候,偏转角度的数据集不够,那就将正常的数据集左转15度,右转15度,类似这样的处理。
模型选择
现在在偏差和方差之间需要一个权衡,想选择的模型,可以平衡偏差和方差产生的错误,使总错误最小,但是下面这件事最好不要做:
手上有Training set 和Testing set,想要知道model1、model2、model3中选哪一个,分别用model1、model2、model3找一个best function,然后派到testing set上,分别得到error1、error2、error3,比较它们,选取error值最小的。
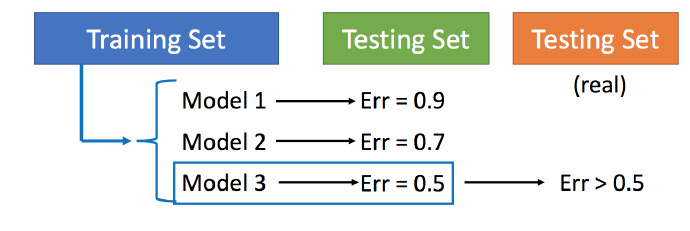
- 用训练集训练不同的模型,然后在测试集上比较error
模型3的错误比较小,就认为模型3好。但实际上这只是你手上的测试集,真正完整的测试集并没有。比如在已有的测试集上错误是0.5,但有条件收集到更多的测试集后通常得到的错误都是大于0.5的。 (不是很懂)
交叉验证

图中public的测试集是已有的,private是没有的。交叉验证就是将训练集再分为两部分,一部分作为训练集,一部分作为验证集。用训练集训练模型,然后在验证集上比较,确定出最好的模型之后(比如模型3),再用全部的训练集训练模型3,然后再用public的测试集进行测试,此时一般得到的错误都比较大。此时会想再回去调参数,调整模型,让在public的测试集上更好,但不推荐这样。
若担心将训练集拆分的时候分的效果比较差,可以用下面的方法。
N折交叉验证
将训练集分成N份(比如分成3份)。

比如在三份中训练结果Average错误是模型1最好,再用全部训练集训练模型1。
2. 梯度下降
什么是梯度下降?
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
简单说就是从山顶上找一个最快,最陡峭的路线下山。
梯度下降法用以下面的最优化问题:
(损失函数)
(参数)
我们要找一组参数 ,让损失函数越小越好,这个问题可以用梯度下降法解决:
假设有里面有两个参数
,随机选取初始值
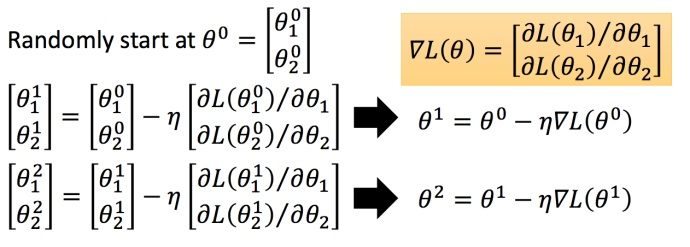
:学习率

将梯度下降法的计算过程进行可视化:
调整学习速率
1. 手动调整学习率
例如:
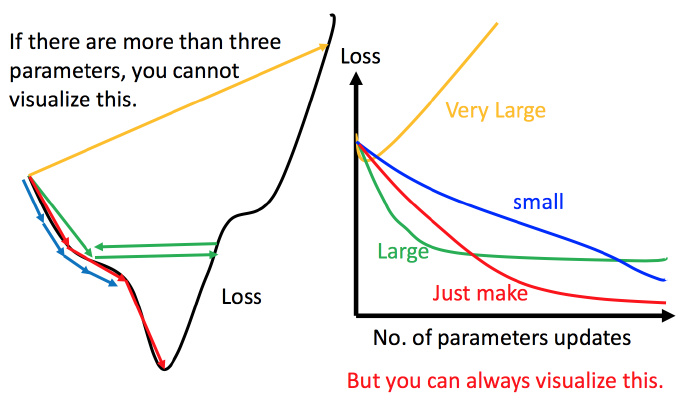
黑色:损失函数的曲线
- 假设从左边最高点开始,如果学习率刚好,比如红线,就能顺利找到最低点。
- 如果学习率太小,比如蓝线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。
- 如果学习率有点大,比如绿线,就会在上面震荡,走不下去,永远无法到达最低点。
- 如果学习率非常大,比如黄线,直接飞出去,更新参数的时候只会发现损失函数越更新越大。
可视化适合参数是一维或二维,更高维的情况无法可视化。
2. 自适应学习率
简单的思想:随着次数的增加,通过一些因子来减少学习率
-
通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
-
update好几次参数之后,比较靠近最低点,此时减少学习率
-
比如
,
是次数。随着次数的增加,
减小
学习率不能一个值通用所有特征,不同的参数需要不同的学习率
3. Adagrad 算法
每个参数的学习率都除以之前微分的均方根
普通的梯度下降:
是一个参数
Adagrad :
:之前参数的所有微分的均方根,对于每个参数都不一样
举例:
参数更新过程:
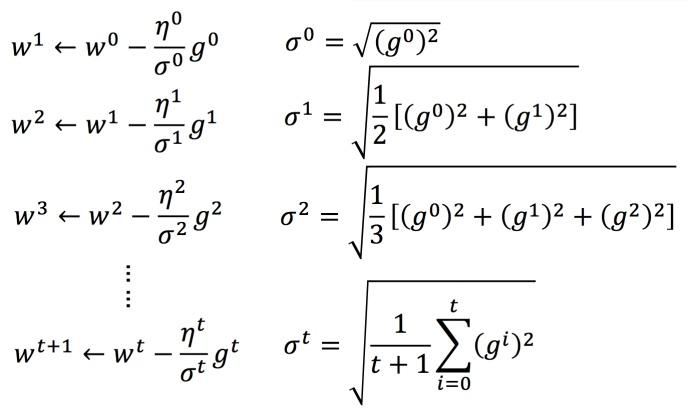
简化过程为: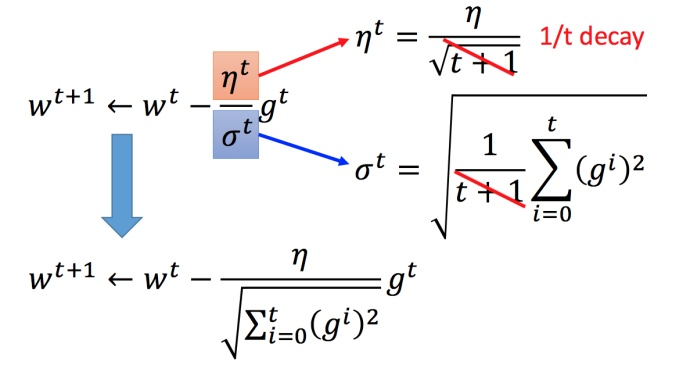
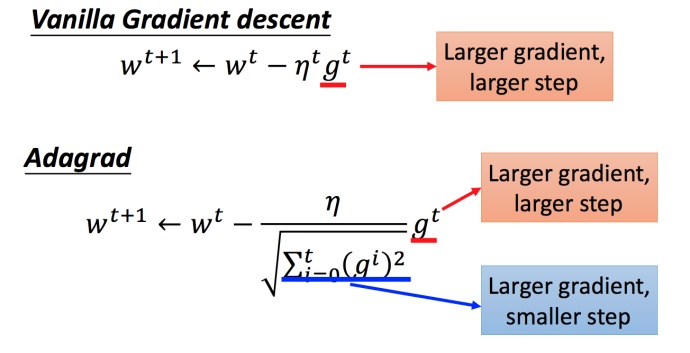
在 Adagrad 中,当梯度()越大,步伐应该越大,但分母导致当梯度越大的时候,步伐会越小。
直观解释:
,

正式解释: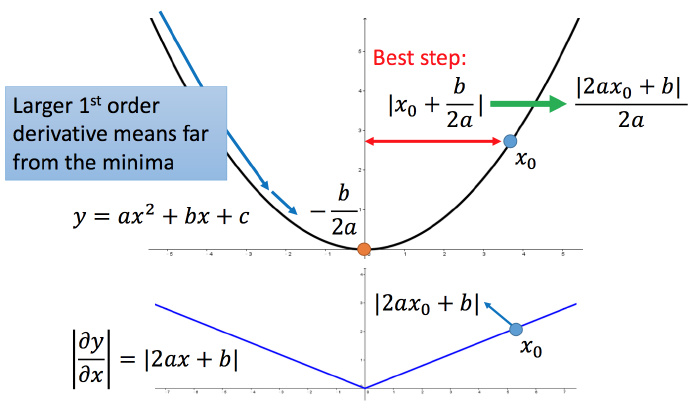
比如初始点在,最低点为
,最佳的步伐就是
到最低点之间的距离
,也可以写成
。而刚好
就是方程绝对值在
这一点的微分。
这样可以认为,如果算出来的微分越大,则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比,它可能是比较好的。
结论1-1:梯度越大,距最低点越远。
这个结论在多个参数的时候就不一定成立了。
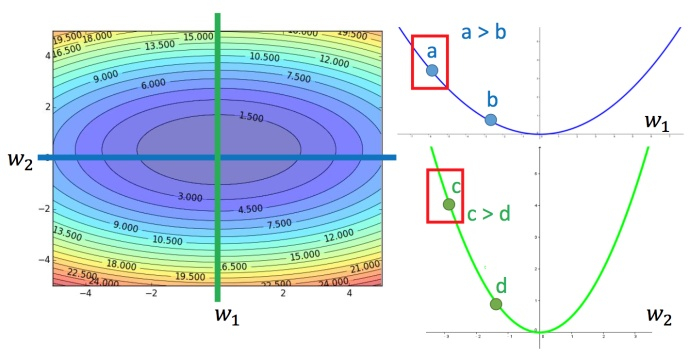
上图左边是两个参数的损失函数,颜色代表损失函数的值。如果只考虑参数,就像图中蓝色的线,得到右边上图结果;如果只考虑参数
,就像图中绿色的线,得到右边下图的结果。对于a和b,结论1-1是成立的,同理c和b也成立。但是如果对比a和c,就不成立了,c比a大,但c距离最低点是比较近的。
最好的step应该考虑到二次微分:
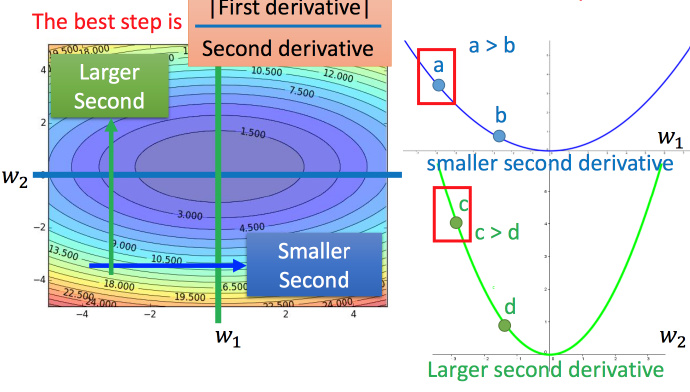
进一步解释Adagrad
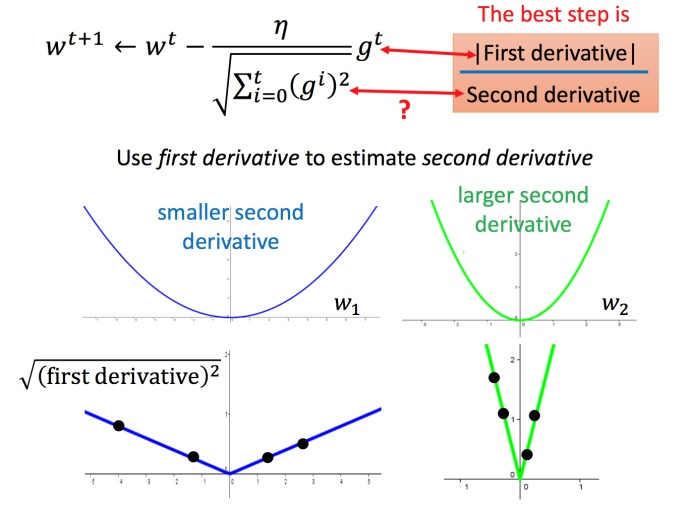
对于就是希望再尽可能不增加过多运算的情况下模拟二次微分。(如果计算二次微分,在实际情况中可能会增加很多的时间消耗)
随机梯度下降法

:第n个example的Lossfunction。
:对第n个example的Lossfunction的gradient。
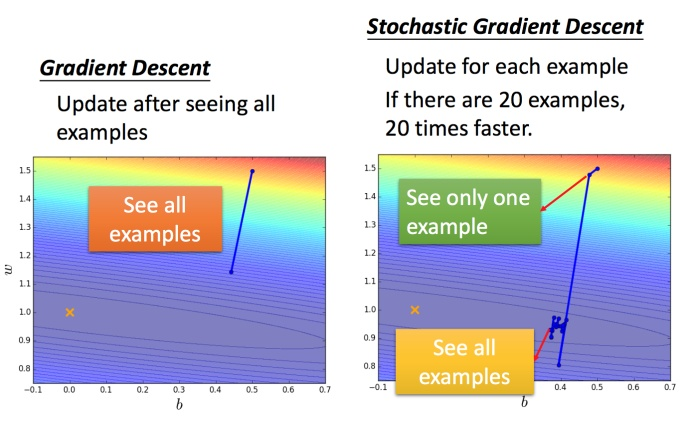
常规梯度下降法走一步要处理到所有二十个example,但随机算法此时已经走了二十步(每处理一个example就更新)
特征缩放
例如:
两个输入的分布的范围很不一样,建议把他们的范围缩放,使得不同输入的范围是一样的。

为什么要这样做?
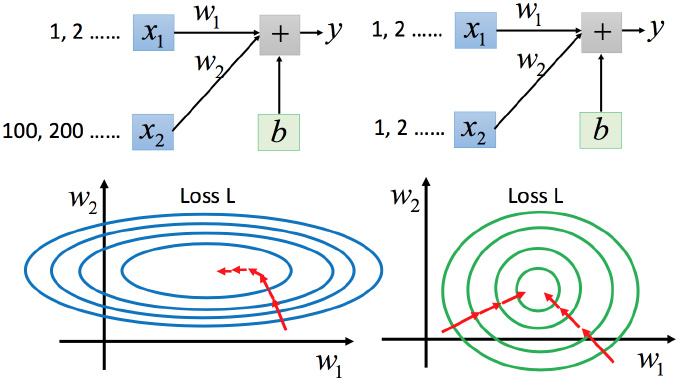
上图左边是的scale比
要小很多,所以当
和
做同样的变化时,
对y的变化影响是比较小的,
对y的变化影响是比较大的。
上图右边是两个参数scaling比较接近,右边的绿色图接近圆形。对于左边的情况,上面讲过这种狭长的情形若不用Adagrad比较难处理,两个方向上需要不同的学习率,同一组学习率搞不定。而右边情形更新参数比较容易。左边的梯度下降并不是向着最低点方向走的,而是顺着等高线切线法线方向走的。但绿色就可以向着圆心(最低点)走,这样做参数更新也比较有效率。
怎么做缩放?
方法非常多,举一种常见做法:
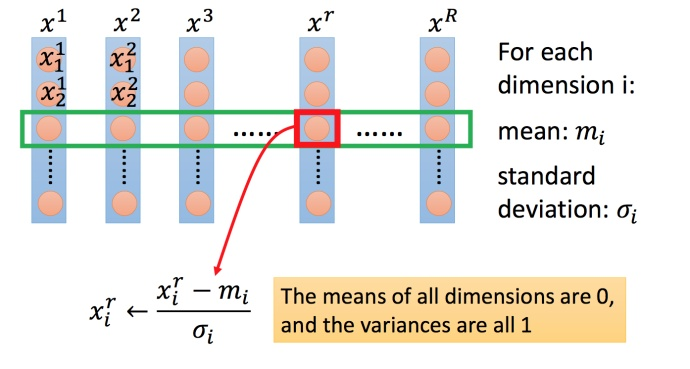
上图每一列都是一个例子,里面都有一组特征。
对每一个维度(绿色框)
- 计算平均数,记做
;
- 计算标准差,记做
;
用第个例子中的第
个输入
,减掉平均数
,然后除以标准差
,得到的结果是所有的维数都是0,所有的方差都是1。
























 403
403











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










