数据导入与预处理-拓展-pandas时间数据处理03

IT从业者张某某

已于 2024-03-22 15:29:50 修改

阅读量1.2k

点赞数 12

分类专栏：数据导入与预处理课程配套资源HM 文章标签： pandas python 开发语言

于 2022-10-22 11:32:49 首次发布

本文链接：https://blog.csdn.net/m0_38139250/article/details/127459593

版权

数据导入与预处理课程配套资源HM 专栏收录该内容

21 篇文章 6 订阅

订阅专栏

数据导入与预处理-拓展-pandas时间数据处理03

Pandas时序数据系列博客
1. 时间序列数据
- 1. 1 时间序列概述
2. 时序数据分析

Pandas时序数据系列博客

数据导入与预处理-拓展-pandas时间数据处理01
数据导入与预处理-拓展-pandas时间数据处理02
数据导入与预处理-拓展-pandas时间数据处理03
备注：如果有帮助，欢迎点赞收藏评论一键三联哈~~

参考博客：
知乎作者：景略集智
微信公众号：优达学城

1. 时间序列数据

1. 1 时间序列概述

百科中关于时间序列的描述为：

时间序列（或称动态数列）是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列。时间序列分析的主要目的是根据已有的历史数据对未来进行预测。经济数据中大多数以时间序列的形式给出。根据观察时间的不同，时间序列中的时间可以是年份、季度、月份或其他任何时间形式

时间序列的构成要素：

构成要素：长期趋势，季节变动，循环变动，不规则变动。
1）长期趋势（T）现象在较长时期内受某种根本性因素作用而形成的总的变动趋势。
2）季节变动（S）现象在一年内随着季节的变化而发生的有规律的周期性变动。
3）循环变动（C）现象以若干年为周期所呈现出的波浪起伏形态的有规律的变动。
4）不规则变动（I）是一种无规律可循的变动，包括严格的随机变动和不规则的突发性影响很大的变动两种类型。

金融市场中，时序数据十分常见，我们购买股票，虚拟货币，一定会获得收益吗？实际上我们没法保证一定会有很好的收益，但可以根据之前的股票/虚拟货币价格估算出近似价值。时序模型就是预测这些值的一种方式。
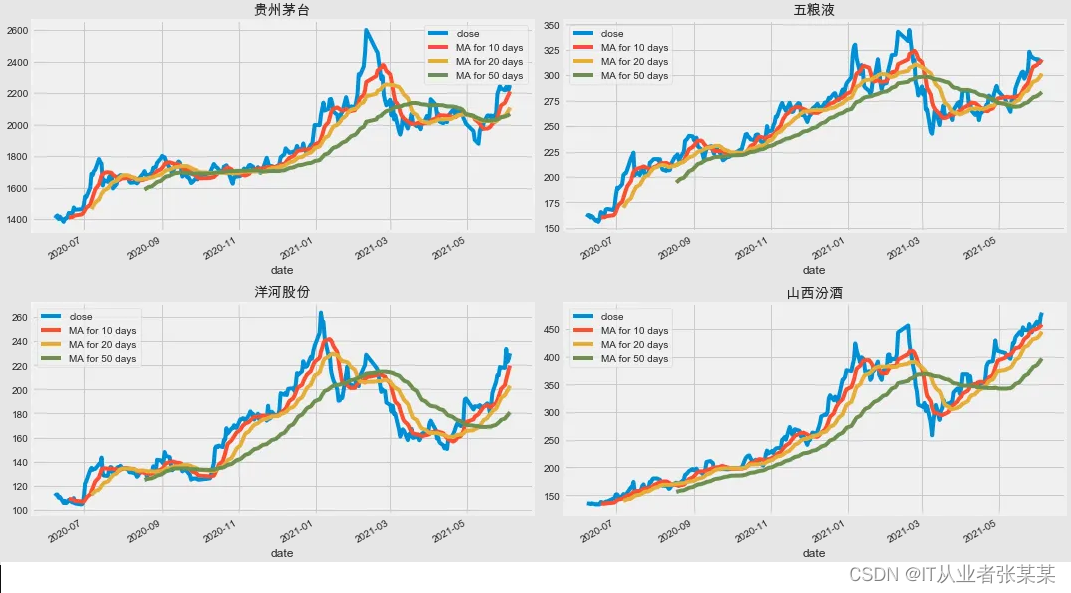
在这里插入图片描述
除此之外在很多重要的领域，比如预测太阳活动和海洋潮汐、预测某公司接下来一年的销售额，工业领域预测下个月的能源消耗等，都是根据之前每年、每月和每天的数据，预测接下来的值，这些都是可以用时间序列的应用。

2. 时序数据分析

本文使用案例为高铁服务商 JetRail 旗下高铁的乘客数量。数据下载地址：
训练集为2012 年 8 月至 2014 年 8月的数据，需要用这些数据预测接下来 7 个月的乘客数量。
实现内容如下：

安装程序库（statsmodels）
方法1——先以朴素法开始
方法2——简单平均数
方法3——移动平均数
方法4——指数平滑法
方法5——霍尔特线性趋势预测
方法6——Holt-Winters季节性预测模型
方法7——自回归移动平均模型

1.2 数据集导入与处理

1. 查看数据

读取训练集数据

import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
#Importing data
df = pd.read_csv('train.csv')
df

输出为：
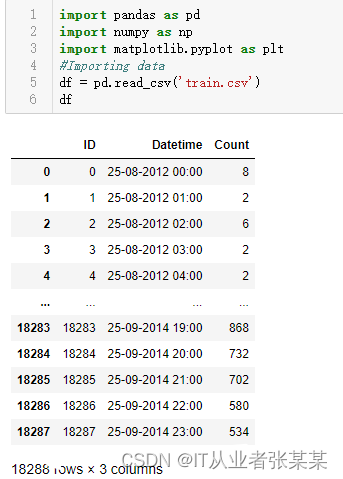
在这里插入图片描述

如上面的输出语句所示，我们获得了 2012-2014 年两年每个小时的乘客数量，然后需要预测未来的乘客数量。

读取测试集数据

df_test = pd.read_csv('Test.csv')
df_test

输出为：
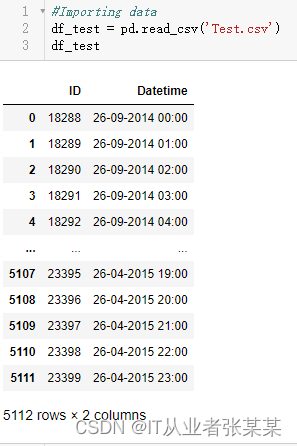
在这里插入图片描述

查看训练集类型

df.info()

输出为：
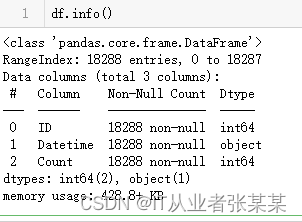
在这里插入图片描述

可以看到空缺值，类型信息，

2. 数据处理

把Datetime一列转变为时间戳类型

df['Timestamp'] = pd.to_datetime(df['Datetime'],format='%d-%m-%Y %H:%M') 
df

输出为：
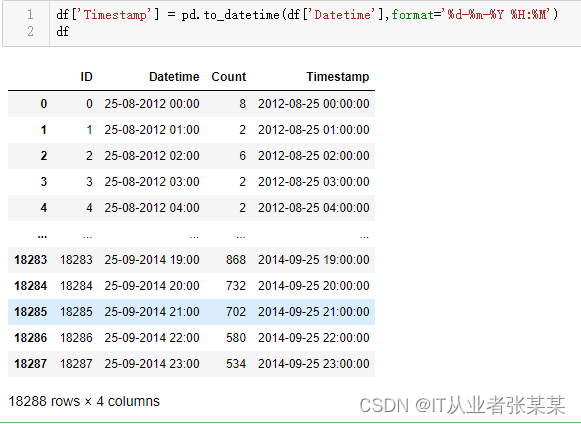
在这里插入图片描述

3. 切分数据集

取部分数据作为数据集，前 14 个月（ 2012 年 8 月- 2013 年 10 月）用作训练数据，后两个月（2013 年 11 月 - 2013 年 12 月）用作测试数据。

为了解释每种方法的不同之处，我以每天为单位构造和聚合了一个数据集。
从 2012 年 8 月- 2013 年 12 月的数据中构造一个数据集。

确定（ 2012 年 8 月- 2013 年 10 月）范围

df[df['Timestamp'] < "2013-10-31 23:59:59 "]

输出为：
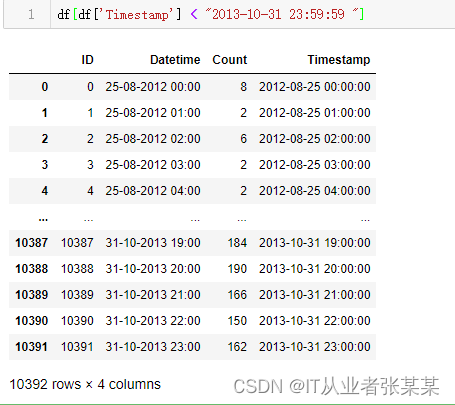
在这里插入图片描述

一共0-10391共10392条数据，10392/24 = 433天

确定（ 2013 年 11 月- 2013 年 12 月）范围

df[(df['Timestamp'] > "2013-10-31 23:59:59 ") & (df['Timestamp'] < "2013-12-31 23:59:59 ")]

输出为：
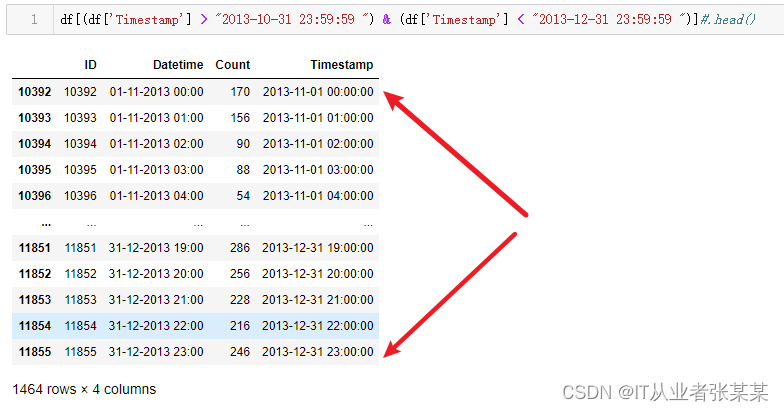
在这里插入图片描述
一共10392-11855共1462条数据，1464/24 = 61天

切分训练集和测试集

train = df[df['Timestamp'] < "2013-10-31 23:59:59 "]
print(train.iloc[10391,:])
test = df[(df['Timestamp'] > "2013-10-31 23:59:59 ") & (df['Timestamp'] < "2013-12-31 23:59:59 ")]
test

输出为：
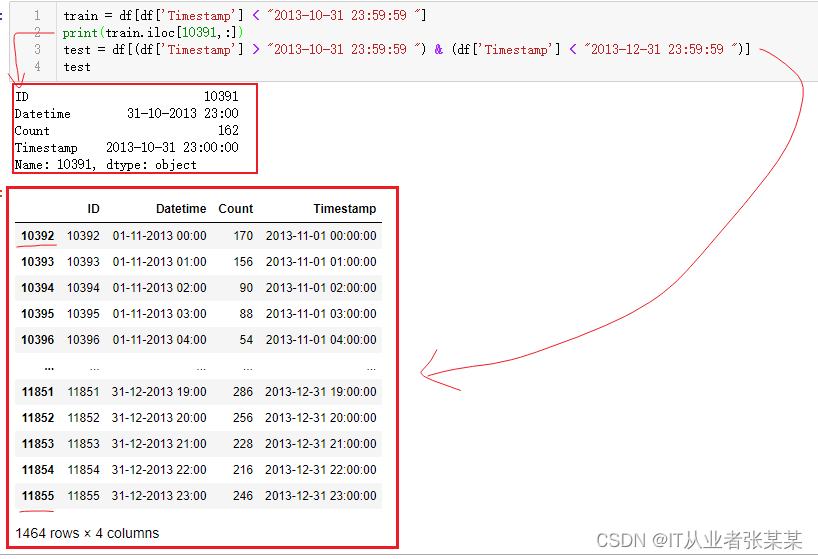
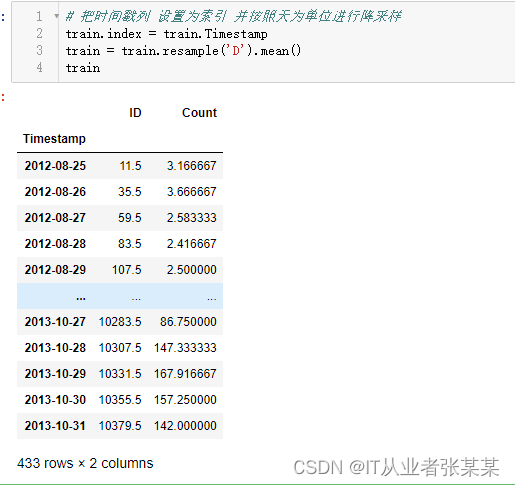
在这里插入图片描述

训练集降采样

# 把时间戳列 设置为索引 并按照天为单位进行降采样
train.index = train.Timestamp 
train = train.resample('D').mean() 
train

输出为：
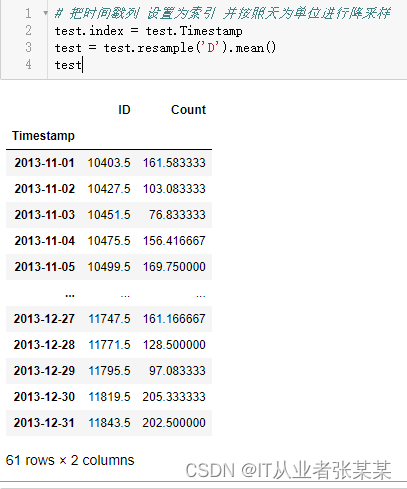
在这里插入图片描述
测试集降采样

# 把时间戳列 设置为索引 并按照天为单位进行降采样
test.index = test.Timestamp 
test = test.resample('D').mean() 
test

输出为：
在这里插入图片描述

4. 数据分析

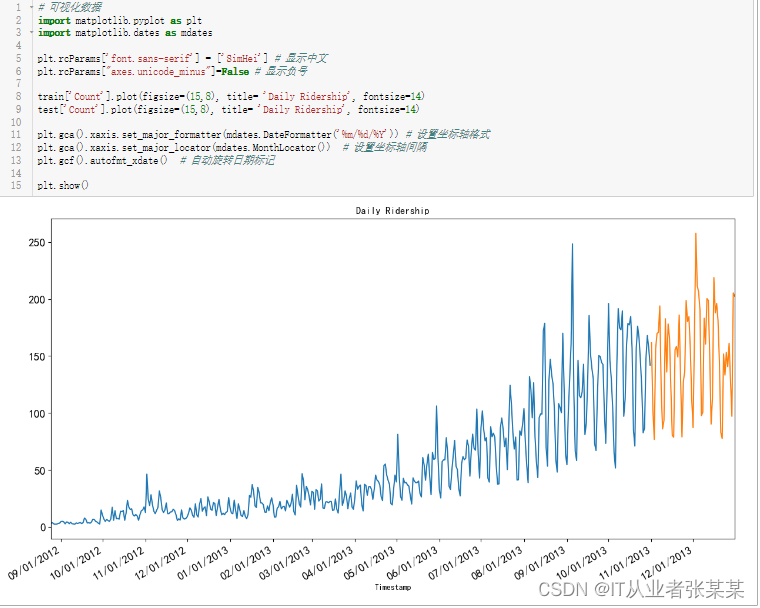
将数据可视化（训练数据和测试数据一起），从而得知在一段时间内数据是如何变化的。

# 可视化数据
import matplotlib.pyplot as plt 
import matplotlib.dates as mdates
 
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
plt.rcParams["axes.unicode_minus"]=False # 显示负号

train['Count'].plot(figsize=(15,8), title= 'Daily Ridership', fontsize=14)
test['Count'].plot(figsize=(15,8), title= 'Daily Ridership', fontsize=14)

plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%m/%d/%Y')) # 设置坐标轴格式
plt.gca().xaxis.set_major_locator(mdates.MonthLocator())  # 设置坐标轴间隔
plt.gcf().autofmt_xdate()  # 自动旋转日期标记

plt.show()

输出为：
在这里插入图片描述

1.3 时间序列分析

1. 安装程序库（statsmodels）

安装：

 pip install statsmodels -i https://pypi.tuna.tsinghua.edu.cn/simple

测试：

 from statsmodels.tsa.api import ExponentialSmoothing

不报错，即为安装正常

2. 方法1：先以朴素法开始

一般来说，短时间内的数据往往是平稳的，我们往往可以根据昨天的数据去预测预测第二天的值，即把明天的数据当成与今天是相同的。这种假设第一个预测点和上一个观察点相等的预测方法就叫朴素法。
$Hence\widehat{y}_{t+1} = y_{t}$
用朴素法预测：

dd= np.asarray(train.Count)
y_hat = test.copy()
y_hat['naive'] = dd[len(dd)-1]
plt.figure(figsize=(12,8))
plt.plot(train.index, train['Count'], label='Train')
plt.plot(test.index,test['Count'], label='Test')
plt.plot(y_hat.index,y_hat['naive'], label='Naive Forecast')
plt.legend(loc='best')
plt.title("Naive Forecast")
plt.show()
y_hat

输出为：
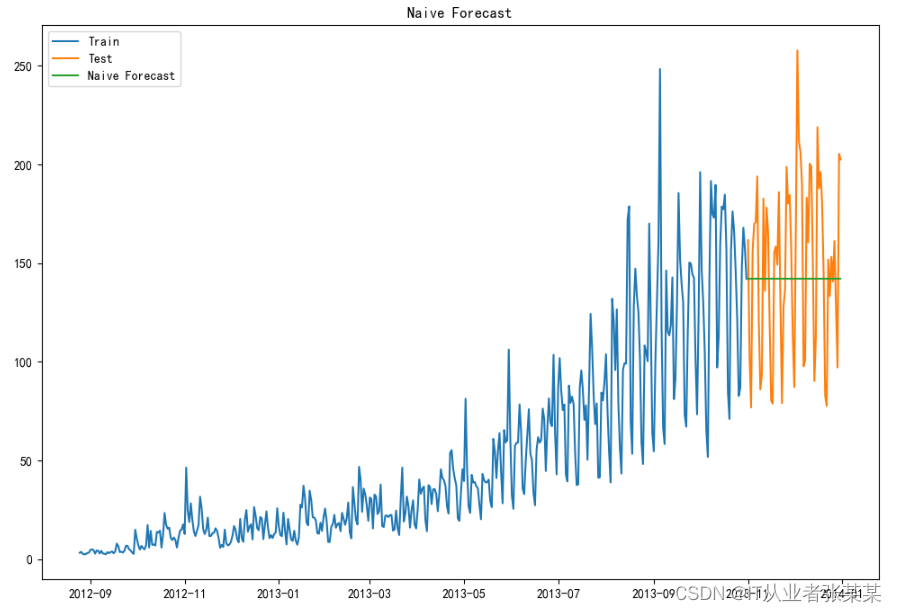
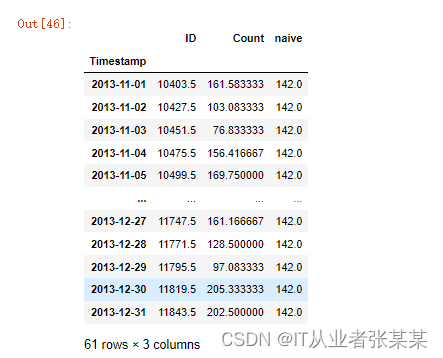
在这里插入图片描述
我们下面计算均方根误差，检查模型在测试数据集上的准确率。

from sklearn.metrics import mean_squared_error
from math import sqrt
rms = sqrt(mean_squared_error(test.Count, y_hat.naive))
rms

输出为：
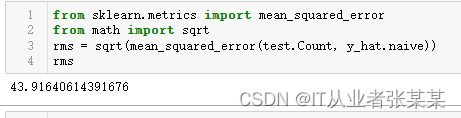
在这里插入图片描述

从均方根误差值以及上面的图表可以看出，朴素法并不适合变化很大的数据集，最适合稳定性很高的数据集。我们还可以用不同的方法优化结果。下面我们试试其它方法。

3. 方法2：简单平均法

将预期值等同于之前所有观测点的平均值的预测方法就叫简单平均法.
$Hence\widehat{y}_{x+1}=\dfrac{1}{x}\sum ^{x}_{i=1}y_{i}$

y_hat_avg = test.copy()
y_hat_avg['avg_forecast'] = train['Count'].mean()
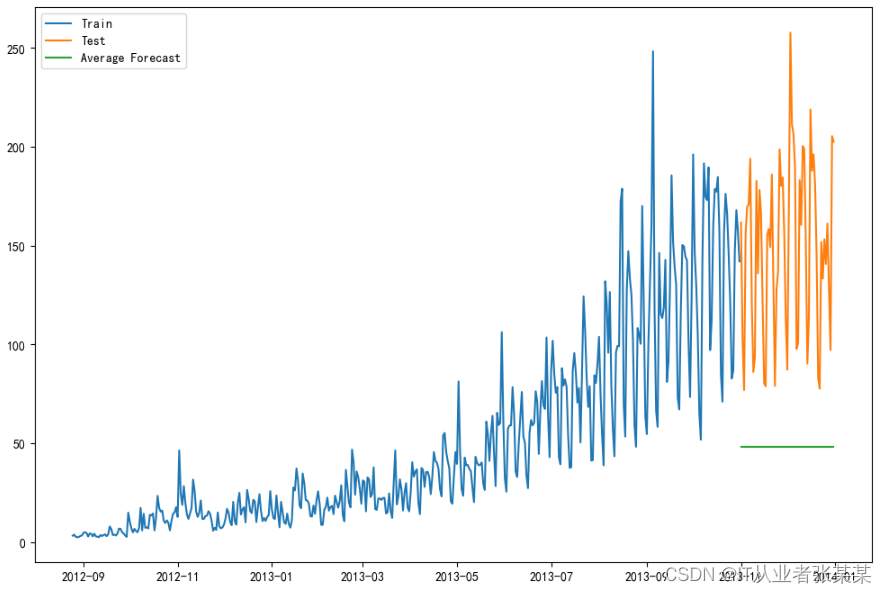
plt.figure(figsize=(12,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['avg_forecast'], label='Average Forecast')
plt.legend(loc='best')
plt.show()
y_hat_avg

输出为：
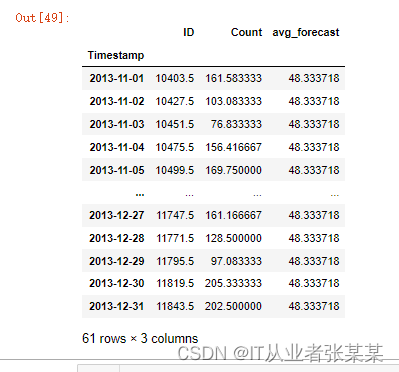在这里插入图片描述计算均方根误差值，检查模型的准确率。

rms = sqrt(mean_squared_error(test['Count'], y_hat_avg['avg_forecast']))
rms

输出为：
在这里插入图片描述

4. 方法3——移动平均法

之前的简单平均法，使用所有先前数据的平均值，这有些不合理，如果基于某窗口期的平均值预测下一段的值，这就是移动平均法。
假设"滑动窗口"的大小值p，使用简单的移动平均模型，我们可以根据之前数值的固定有限数p的平均值预测某个时序中的下一个值。这样，对于所有的 i > p
$\widehat{y}_{i}=\dfrac{1}{p} \left( y_{i-1}+y_{i-2}+...+y_{i-p} \right)$

y_hat_avg = test.copy()
y_hat_avg['moving_avg_forecast'] = train['Count'].rolling(60).mean().iloc[-1] # 窗口为60 求均值 最后一个 131.761111
plt.figure(figsize=(16,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['moving_avg_forecast'], label='Moving Average Forecast')
plt.legend(loc='best')
plt.show()

输出为：
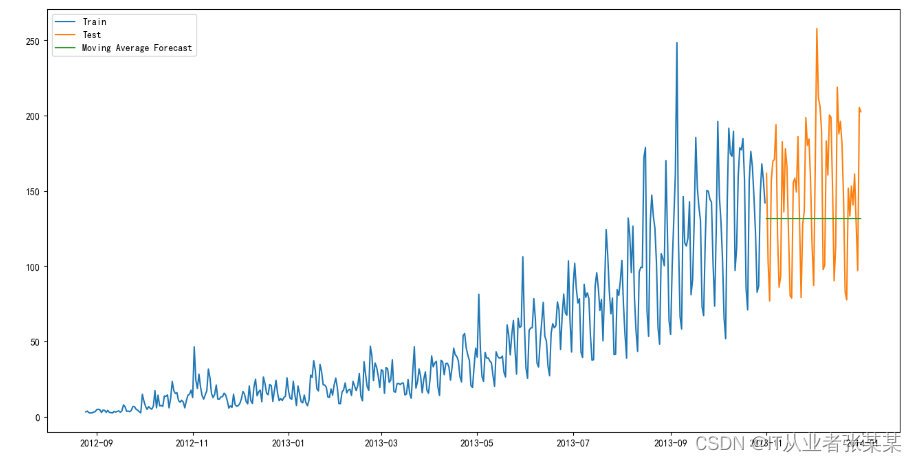
在这里插入图片描述
只选择过去两个月的数据。现在计算均方根误差值，检查模型的准确度。

rms = sqrt(mean_squared_error(test['Count'], y_hat_avg['moving_avg_forecast']))
rms

输出为：
在这里插入图片描述
在移动平均法中，各个时间的权重是一致的，如果考虑到不同时间的观察值有着不同的权重，就叫做加权移动平均法。

加权移动平均法其实还是一种移动平均法，只是“滑动窗口期”内的值被赋予不同的权重，通常来讲，最近时间点的值发挥的作用更大了。

5. 方法4——简单指数平滑法

简单指数平滑法与加权移动平均法类似，但权重随着观测值从早期到晚期的变化呈指数级下降，最小的权重和最早的观测值相关：
$\widehat{y}_{T+1|T}=\alpha y_{T}+\alpha \left( 1-\alpha \right) y_{T -1} +\alpha \left( 1-\alpha \right)^{2}y_{T-2} +...$

其中 $\alpha <1$ 是平滑参数。对时间点T+1的单步预测值是时序 $y_{1},...y_{T}$ 所有观察值的加权平均值。

from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt
y_hat_avg = test.copy()
fit2 = SimpleExpSmoothing(np.asarray(train['Count'])).fit(smoothing_level=0.6,optimized=False)
y_hat_avg['SES'] = fit2.forecast(len(test))
plt.figure(figsize=(16,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SES'], label='SES')
plt.legend(loc='best')
plt.show()
y_hat_avg

输出为：
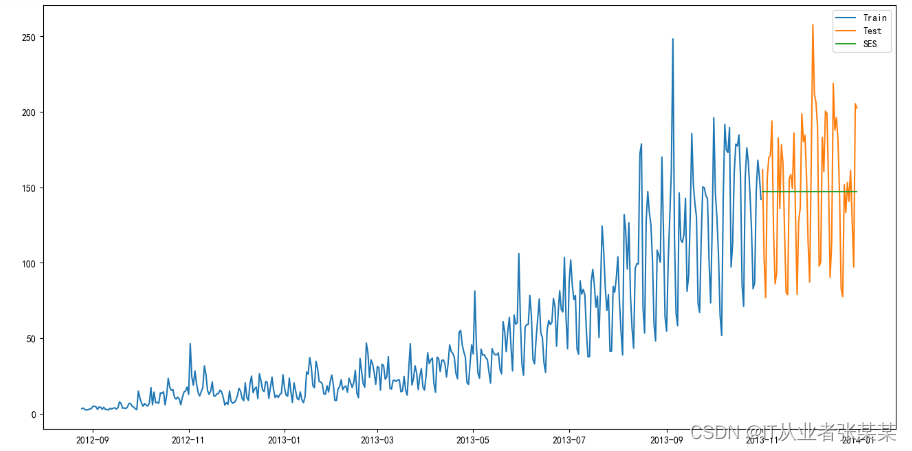
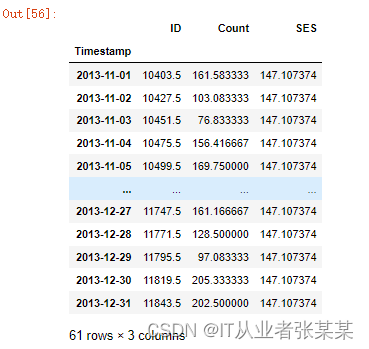
在这里插入图片描述
计算均方根误差

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.SES))
rms

输出为：
在这里插入图片描述

6. 方法5——霍尔特线性趋势法

以上几种方法在波动性较大的数据集上表现不够友好，如果未来趋势是逐渐上涨的，我们需要考虑这种趋势。
每个时序数据集可以分解为相应的几个部分：趋势，季节性和残差。任何呈现某种趋势的数据集都可以用霍尔特线性趋势法用于预测。

import statsmodels.api as sm

sm.tsa.seasonal_decompose(train.Count).plot()
result = sm.tsa.stattools.adfuller(train.Count)
plt.show()
result

输出为：
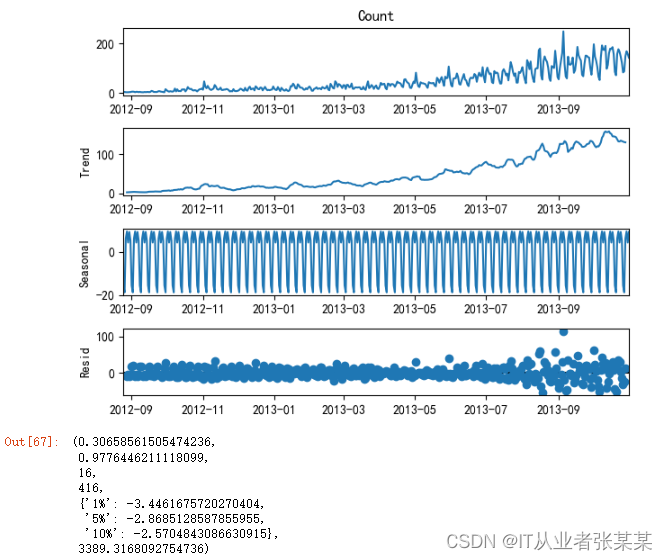
在这里插入图片描述

我们从图中可以看出，该数据集呈上升趋势。因此我们可以用霍尔特线性趋势法预测未来价格。
该算法包含三个方程：一个水平方程，一个趋势方程，一个方程将二者相加以得到预测值 ŷ ：
$e_{t}=\alpha y _{t}+\left( 1- \alpha \right) \left( e_{t-1}+b_{t-1}\right)$
$b_{t}=\beta \left( e_{t}- e_{t-1} \right) +\left( 1- \beta \right) \left( b_{t-1}\right)$
$\widehat{y}_{t+h|t}=e_{t}+hb_{t}$

上述方程中，水平方程显示它是观测值和样本内单步预测值的加权平均数，趋势方程显示它是根据 e(t)−e(t−1) 和之前的预测趋势 b(t−1) 在时间t处的预测趋势的加权平均值。

我们将这两个方程相加，得出一个预测函数。我们也可以将两者相乘而不是相加得到一个乘法预测方程。当趋势呈线性增加和下降时，我们用相加得到的方程；当趋势呈指数级增加或下降时，我们用相乘得到的方程。实践操作显示，用相乘得到的方程，预测结果会更稳定，但用相加得到的方程，更容易理解。

y_hat_avg = test.copy()
 
fit1 = Holt(np.asarray(train['Count'])).fit(smoothing_level = 0.3,smoothing_trend = 0.1)
y_hat_avg['Holt_linear'] = fit1.forecast(len(test))
 
plt.figure(figsize=(16,8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_linear'], label='Holt_linear')
plt.legend(loc='best')
plt.show()
y_hat_avg

输出为：
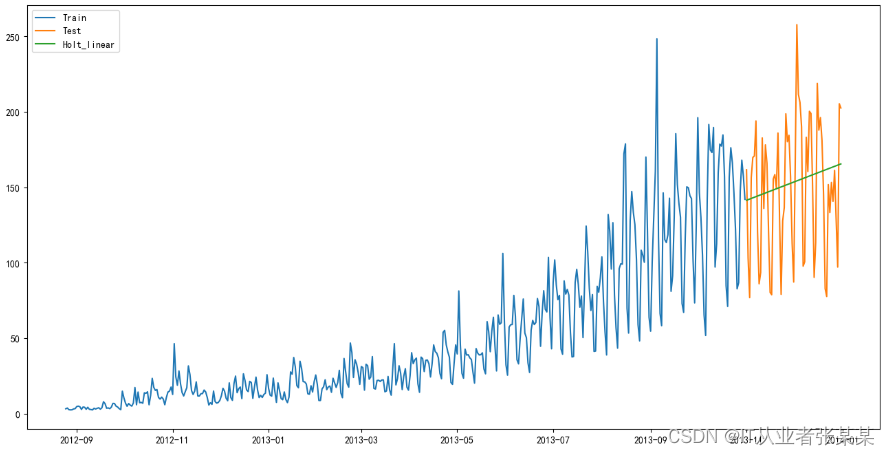
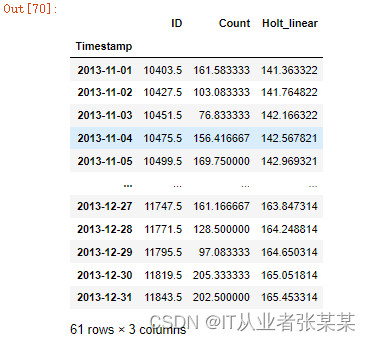
在这里插入图片描述

均方根误差，检查模型的准确率：

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.Holt_linear))
rms

输出为：
在这里插入图片描述

7. 方法6——Holt-Winters季节性预测模型

针对时间序列数据，如果数据实体具有季节性，那么该数据集就具有季节性。
前面讨论的5种模型在预测时并没有考虑到数据集的季节性，因此我们需要一种能考虑这种因素的方法。
应用到这种情况下的算法就叫做Holt-Winters季节性预测模型，它是一种三次指数平滑预测，其背后的理念就是除了水平和趋势外，还将指数平滑应用到季节分量上。
Holt-Winters季节性预测模型由预测函数和三次平滑函数——一个是水平函数ℓt，一个是趋势函数bt，一个是季节分量 st，以及平滑参数 α, β 和 γ。
在这里插入图片描述
水平函数为季节性调整的观测值和时间点t处非季节预测之间的加权平均值。趋势函数和霍尔特线性方法中的含义相同。季节函数为当前季节指数和去年同一季节的季节性指数之间的加权平均值。

在本算法，我们同样可以用相加和相乘的方法。当季节性变化大致相同时，优先选择相加方法，而当季节变化的幅度与各时间段的水平成正比时，优先选择相乘的方法。

y_hat_avg = test.copy()
fit1 = ExponentialSmoothing(np.asarray(train['Count']) ,seasonal_periods=7 ,trend='add', seasonal='add',).fit()
y_hat_avg['Holt_Winter'] = fit1.forecast(len(test))
plt.figure(figsize=(16,8))
plt.plot( train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['Holt_Winter'], label='Holt_Winter')
plt.legend(loc='best')
plt.show()
y_hat_avg

输出为：
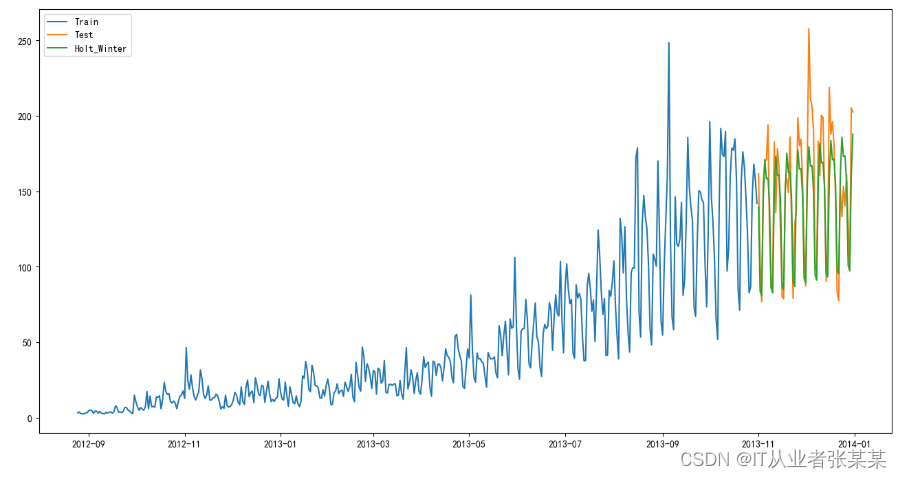
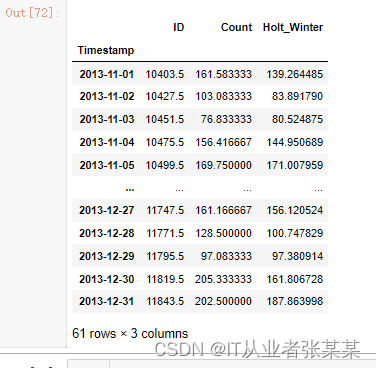
在这里插入图片描述
均方根误差，看看模型的准确度

# 我们现在计算一下均方根误差，看看模型的准确度。
rms = sqrt(mean_squared_error(test.Count, y_hat_avg.Holt_Winter))
rms

输出为：
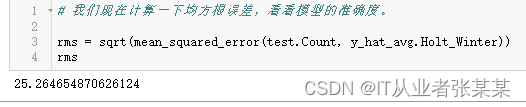
在这里插入图片描述
看到趋势和季节性的预测准确度都很高。我们选择了 seasonal_period = 7作为每周重复的数据。也可以调整其它其它参数，我在搭建这个模型的时候用的是默认参数。你可以试着调整参数来优化模型。

8. 方法7——自回归移动平均模型

参考：石晓文
另一个场景的时序模型是自回归移动平均模型（ARIMA）。指数平滑模型都是基于数据中的趋势和季节性的描述，而自回归移动平均模型的目标是描述数据中彼此之间的关系。ARIMA的一个优化版就是季节性ARIMA。它像Holt-Winters季节性预测模型一样，也把数据集的季节性考虑在内。

ARIMA算法模型主体包括三大部分：AR，I以及MA模型。其中，每一个模型部分都拥有一个相关的模型参数—ARIMA（p，d，q）。算法的基本原理是将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。

差分法平稳数据

train['Count_diff_1'] = train['Count'].diff(1)
train['Count_diff_2'] = train['Count_diff_1'].diff(1)
fig = plt.figure(figsize=(6,12))
ax1 = fig.add_subplot(311)
ax1.plot(train['Count'])
ax2 = fig.add_subplot(312)
ax2.plot(train['Count_diff_1'])
ax3 = fig.add_subplot(313)
ax3.plot(train['Count_diff_2'])
ax1.set_title("原始")
ax2.set_title("1阶")
ax3.set_title("2阶")
plt.show()
train['Count_diff_2']

输出为：
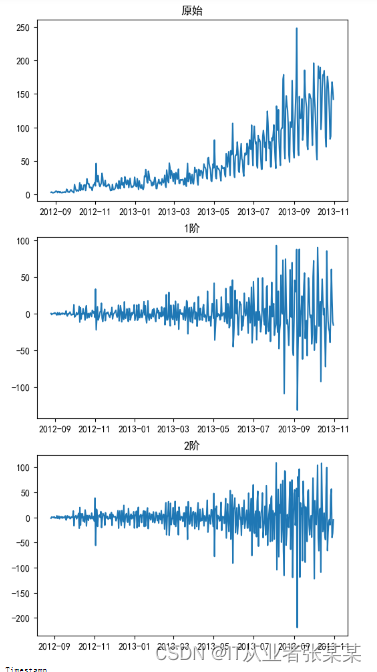
在这里插入图片描述

在ARIMA（p，d，q）整体模型中，AR是自回归模型，对应的模型参数p为自回归项数；I为差分模型，对应的模型参数d为使之成为平稳时间序列所做的差分次数（阶数）；MA为滑动平均模型，q为滑动平均项数。在实际进行算法模型的构建时，可以根据ACF自相关系数图决定q的取值，PACF偏自相关系数图决定p的取值。

y_hat_avg = test.copy()
fit1 = sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4),seasonal_order=(0,1,1,7)).fit()
y_hat_avg['SARIMA'] = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)
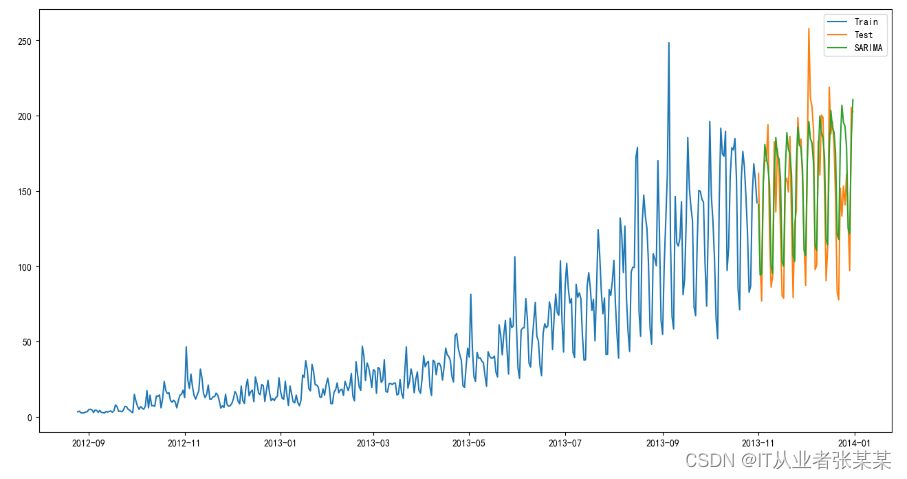
plt.figure(figsize=(16,8))
plt.plot( train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.show()
y_hat_avg

输出为：
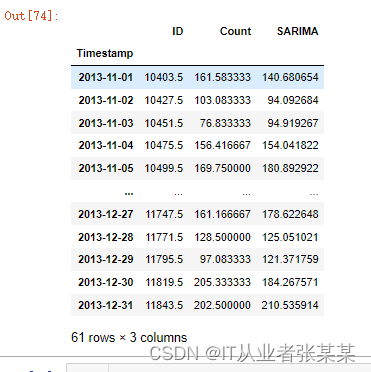
在这里插入图片描述
均方根误差

# 计算一下均方根误差，看看模型的准确度。

rms = sqrt(mean_squared_error(test.Count, y_hat_avg.SARIMA))
rms

输出为：
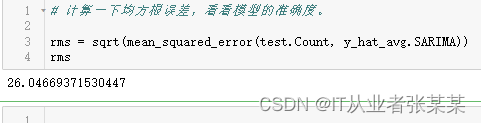
在这里插入图片描述
我们可以看到使用季节性 ARIMA 的效果个 Holt-Winters 一样好。我们根据 ACF 和 PACF 图选择参数。如果你为 ARIMA 模型选择参数时遇到了困难，可以用 R 语言中的 auto.arima。

最后，我们将这几种模型的准确度比较一下：

Model	RMSE
朴素法	43.9
简单平均法	109.9
移动平均法	46.72
简单指数	43.35
霍尔特线性趋势	43.05
Holt-Winters季节预测	25.26
自回归移动平均ARIMA	26.05