医学成像系统2020X射线断层成像仿真实验

实验报告已经上传资源~

1实验内容

（1）掌握X射线计算机断层扫描成像系统的成像原理；
（2）了解并能运用不同断层成像重建的算法；
（3）使用MATLAB代码实现其功能；
（4）进一步掌握X射线断层成像原理。

2实验内容

（1）对一幅仿体断层图像f(x, y)进行平行束扫描；
（2）求投影后的正弦图；
（3）分别利用傅里叶重建法、直接反投影法、滤波反投影法/卷积反投影法对投影后的正弦图进行重建，分别得到重构图像f＇(x, y) ；
（4）比较重构图像f＇(x, y)与原图像f(x, y)的差异，改变实验参数并讨论分析影响重构精度的因素。 

3实验原理

X-CT的实质是基于投影数据重建人体内的断层图像。在CT成像中，物体对X射线的吸收起主要作用，在均匀物体中，X射线的衰减服从指数规律。在X射线穿透人体器官或组织时，由于人体器官或组织是由多种物质成分和不同的密度构成的，所以各点对X射线的吸收系数是不同的。将沿着X射线束通过的物体分割成许多小单元体（体素），令每个体素的厚度均为L。设L足够小，使得每个体素均匀，每个体素的吸收系数为常值，如果X射线的入射强度I0、透射强度I和物体体素的厚度L均为已知，沿着X射线通过路径上的吸收系数之和μ1＋μ2＋……＋μn就可计算出来。

3.1Randon变换

Radon变换是一个积分变换，它将定义在二维平面上的一个函数f(x, y)沿着平面上的任意一条直线做线积分，就相当于对函数f(x, y)做CT扫描。
Radon变换后产生一个极坐标系统，而将𝑝(𝜃)以R-θ直角坐标显示的图像即为正弦图。正弦图可以以图像的方式表示f(x, y)进行变换后的多角度投影数据𝑝(𝑅, 𝜃)。

3.2图像重建

二维图像的投影，就是射线以一定角度穿透物体的衰减值。图像重建的过程包含反投影，就是由这些不同角度（0~180°）下的投影值恢复原始图像。恢复的方法有很多种。下图概括了各种空间的转换关系。

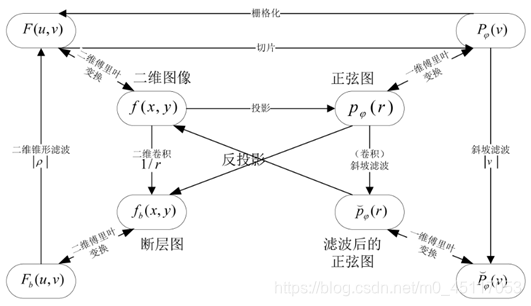
4实验步骤

4.1加载仿体断层图像

在MATLAB中使用phantom生成头部模型的图像，可用于测试radon和iradon或其他二维重建算法的数值准确性。P是由一个大椭圆（代表大脑）和几个较小的椭圆（代表大脑特征）组成的灰度图像作为原始仿体图像f(x, y)。调用公式如下：
P = phantom(def, n)
其中字符型参数def指定要生成的头部模型的类型，在X射线断层扫描中采用 ‘Modified Shepp-Logan’’，因为Modified Shepp-Logan是Sheep-Logan 幻影的变体，其对比度得到了改进，有更好的视觉效果；并n指定模型图像中的行数和列数，取默认值为256。

4.2平行投影

在MATLAB中编写程序投影。使用如下Radon函数对仿体断层图像f(x, y)进行Radon变换，模拟平行束扫描。
[R,Xp]=radon（I，theta，N）
其中，如果theta是标量，返回R是列向量 ，表示theta角度下图像I的radon变换。如果theta是向量，返回R是矩阵，每一列表示某一theta角度下图像I 的Radon变换。我这里的theta统一使用向量形式。

4.3显示投影

在极坐标系中画投影正弦图。横坐标为ρ，纵坐标为θ。设置投影角度个数为180，每隔1°投影一次。

4.4图像重建

分别利用傅里叶重建法、直接反投影法、滤波反投影法/卷积反投影法对投影后的正弦图进行重建，分别得到重构图像f＇(x, y) 。
在这一部分我统一设置投影角度个数为180，每隔1°投影一次。

4.5参数调节及对比分析

比较重构图像f＇(x, y)与原图像f(x, y)的差异，改变实验参数并讨论分析影响重构精度的因素。
我调节了重建效果较好的Ram-Lak窗函数滤波反投影法的投影参数来观察。
在投影角度非常很大的时候，图像失真严重，如图2和3外形几乎完全变形；在投影角度变小的过程中，逐渐的逼近真实图像的形状，但是有较多的伪影。直到增加到180个投影角度时，在空域的振铃现象减弱，清晰度提高。但是与原图相比还是较为模糊。因此我们可以初步得出结论：
增加投影角度可以使得图像逼近原图；投影方向个数与角度是影响重建图像质量的重要参数。

附：MATLAB代码

clc,clear;%清除

P =phantom('Modified Shepp-Logan',256);%P为原图
%Modified Shepp-Logan是Sheep-Logan 幻影的变体，其对比度得到了改进，因此有更好的视觉效果
%画图（取消下一行注释即可画图）
figure,imshow(P),title('Shepp-Logan原始图');

%—————————————————————————————————————
%对仿体断层图像f(x,y)进行平行束扫描；画Radon变换后的正弦图
%使用1°增量
theta = 0:1:179;
%对给定的二维矩形数组生成一组平行射线投影
[R2,xp2] = radon(P,theta);
%先转置数组，然后翻转数组
R2 = flipud(R2');
figure,imshow(R2,[],'XData',xp2([1 end]),'YData',[179 0])
%将坐标轴系统的原点由其默认的左上角移到右下角
axis xy
axis on
%设置 X轴为 θ轴， Y 轴为 ρ 轴
xlabel('\rho'),ylabel('\theta')
%显示投影角度0°下的投影曲线
[R22,xp22] = radon(P,theta);
figure
plot(xp22,R22(:,1))
title('theta=0°时的投影曲线')
%—————————————————————————————————————
%%傅里叶重建法
p_N = 256;                  % 图像默认大小256
theta_N = 180;              % 180度平行投影
pad_N = 1024;               % 投影后变为367*180,每列数据就是当前角度下的投影值。367<512，考虑到傅里叶变换时需要基2对齐，故扩展为1024*180