《鲁棒控制——线性矩阵不等式处理方法》(俞立)第二、三、四章学习笔记

最新推荐文章于 2024-06-25 17:48:56 发布

被巴鸽气晕

最新推荐文章于 2024-06-25 17:48:56 发布

阅读量6.9k

点赞数 17

分类专栏：鲁棒控制 LMI 文章标签：算法线性代数矩阵

本文链接：https://blog.csdn.net/m0_45188205/article/details/120743902

版权

鲁棒控制同时被 2 个专栏收录

1 篇文章 2 订阅

订阅专栏

LMI

1 篇文章 1 订阅

订阅专栏

本文详细介绍了线性矩阵不等式（LMI）在控制系统中的重要角色，包括系统稳定性分析、性能指标评估和控制器设计。LMI用于处理复线性矩阵不等式，转换成标准形式，并应用于连续和离散时间系统的性能分析，如系统增益、能量比和峰值比等。此外，还探讨了状态反馈和输出反馈控制器的综合，以及多目标控制问题，利用LMI工具解决优化问题，确保系统的稳定性和性能要求。

摘要由CSDN通过智能技术生成

第二章线性矩阵不等式

$F(x)<0$ ： $\forall$ 非零向量 $v\in R^n$ , $v^{T}F(x)v<0$ 或者 $F(x)$ 的最大特征值小于0.

$\Phi =\left \{ x:F(x)<0 \right \}$ 是凸集。（设V是数域P上的线性空间，W是V的一个非空子集，如果对W中任意两个向量a,b以及任意0<=c<=1，都有ca+(1-c)b $\in$ W，则W是凸集）。

$F_{1}\left ( x \right )<0,\cdots ,F_{k}\left ( x \right )<0\Leftrightarrow F(x)<0,F(x)=diag\left \{ F_{1}\left ( x \right ),\cdots ,F_{k}\left ( x \right ) \right \}$

schur补性质：

$S\in R^{n\times n}, S=\begin{bmatrix} S_{11} & S_{12}\\ S_{21} &S_{22} \end{bmatrix}$ ，其中 $S_{11}$ 是r*r维的非奇异矩阵，则 $S_{22}-S_{21}S_{11}^{-1}S_{12}$ 称为 $S_{11}$ 在 $S$ 中的Schur补。

对给定的对称矩阵 $S=\begin{bmatrix} S_{11} & S_{12}\\ S_{21} &S_{22} \end{bmatrix},\left ( S_{21}=S_{12}^{T} \right )$ ，其中 $S_{11}$ 是r*r维的非奇异矩阵，则有：

$S<0\Leftrightarrow S_{11}<0,S_{22}-S_{12}^{T}S_{11}^{-1}S_{12}<0\Leftrightarrow S_{22}<0,S_{11}-S_{12}S_{22}^{-1}S_{12}^{T}<0$

复线性矩阵不等式的处理

映射 $a+jb\rightarrow \begin{bmatrix} a &-b \\ -b&a \end{bmatrix}$ ，建立了复数空间C和实矩阵空间 $R^{2\times 2}$ 之间的一个同构关系，因此，复数矩阵M=A+jB可以用实矩阵 $\begin{bmatrix} A &-B \\ -B&A \end{bmatrix}$ 来表示。M=A+jB与N=C+jD的乘积P=X+jY可以表示为 $\begin{bmatrix} X &-Y \\ -Y&X \end{bmatrix}=\begin{bmatrix} A &-B \\ -B&A \end{bmatrix}\begin{bmatrix} C &-D \\ -D&C \end{bmatrix}$

埃尔米特矩阵P=X+jY正定，当且仅当 $\begin{bmatrix} X &-Y \\ -Y&X \end{bmatrix}>0$

一些标准线性矩阵不等式问题

F、G、H是对称矩阵值仿射函数，c是给定的常数向量，标准LMI问题如下：

1. 可行性问题(LMIP)：对于F(x)<0，检验是否存在x，使F(x)<0，存在则可行，否则不可行。

2. 特征值问题(EVP)：在一个LMI约束下，求矩阵G(x)的最大特征值的最小化问题，或确定问题的约束是不可行的。一般形式如下：

$min \lambda$

$\begin{aligned} s.t. \ G(x)&<\lambda I\\ H(x)&<0 \end{aligned}$

可转换为 $min\ c^{T}x\quad s.t.\ F(x)<0$

F(x)<0的LMIP可写成一个EVP： $min\ \lambda \quad s.t.\ F(x)-\lambda I<0$ ，若最小值 $\lambda ^{*}\leq 0$ ，则 $F(x)<0$ 是可行的。

3. 广义特征值问题(GEVP)：在一个LMI约束下，求两个仿射矩阵函数的最大广义特征值的最小化问题（对给定的两个同阶对称矩阵G、F，对标量 $\lambda$ ，如果存在非零向量y，使得 $Gy=\lambda Fy$ ，则 $\lambda$ 称为G、F的广义特征值）。矩阵G、F的最大广义特征值可求解： $min\ \lambda \quad s.t.\ G-\lambda F<0$ ，

当G、F是x的一个仿射函数时，在一个LMI约束下，求矩阵函数G(x)和F(x)的最大广义特征值的最小化问题的一般形式为：

$min\ \lambda$

$\begin{aligned} s.t. \ G(x)&<\lambda F(x) \\F(x)&>0 \\H(x)&<0 \end{aligned}$

（求解LMI问题的算法：椭球法和内点法等。常用S-procedure来将一些不是凸约束的问题转化为线性矩阵不等式约束。）

第三章系统性能分析

系统增益指标

考虑线性时不变的连续时间系统：

$\begin{aligned} \dot{x}(t)=Ax(t)+Bw(t)\\ z(t)=Cx(t)+Dw(t) \end{aligned}$

其中： $x(t)\in R^{n}$ 是系统的状态， $w(t)\in R^{q}$ 是外部扰动输入， $z(t)\in R^{r}$ 是系统被调输出。如果对于某一类外部扰动信号 $w(t)$ ， $z(t)$ 总能保持是“小”的，我们认为这样的系统具有“好”的性能，反映了系统抑制外部扰动的能力。

考虑系统增益 $\Gamma$ ：

$\Gamma =\underset{w\neq 0}{sup}\frac{size(z)}{size(w)}$ 或等价的 $\Gamma =\underset{w}{sup}\left \{ size(z):size(w)\leq 1 \right \}$

$size(\cdot )$ 表示信号 $\cdot$ 的某种度量， $sup$ 表示一个集合的最小上界。 $\Gamma$ 度量了在零初始条件下，对应于最坏扰动输入的系统输出信号 $z$ 的大小。因此，增益越小，系统性能越好，度量方式不同，增益也不同。

对平方可积信号 $f$ ，定义 $||f||_{2}=\left ( \int_{0}^{\infty } ||f(t)||^{2}dt\right )^{1/2}$ （也称为信号 $f$ 的 $L_{2}$ 范数）,其中 $||f(t)||=\sqrt{f^{T}(t)f(t)}$ 是向量的欧式范数。这样定义的 $||f||_{2}$ 正好是信号 $f$ 的能量。

对幅值有界信号 $f$ ，定义 $||f||_{\infty }=\underset{t\geq 0}{sup}||f(t)||$ ,当 $f$ 是一个标量时， $||f||_{\infty }$ 等于 $f$ 的峰值。

可以定义一些性能指标：

IE（Impulse-to-Energy）增益： $\Gamma _{ie}=\underset{\underset{||w_{0}||\leq 1}{w(t)=w_{0}\delta (t)}}{sup}||z||_{2}$

EP（Energy-to-Peak）增益： $\Gamma _{ep}=\underset{||w||_{2}\leq 1}{sup}||z||_{\infty }$

EE（Energy-to-Energy）增益： $\Gamma _{ep}=\underset{||w||_{2}\leq 1}{sup}||z||_{2}$

PP（Peak-to-Peak）增益： $\Gamma _{pp}=\underset{||w||_{\infty}\leq 1}{sup}||z||_{\infty }$

求IE增益定理：如果上述系统是严格真的（D=0）和渐进稳定（A的特征值均有负实部）的，则IE增益有限，且 $\Gamma _{ie}=||B^{T}YB||^{1/2}$ ,其中矩阵的范数取为谱范数，即矩阵的最大奇异值，矩阵Y是以下Lyapunov方程的解：

$YA+A^{T}Y+C^{T}C=0$

IE增益也可以由下式得到：

$\Gamma _{ie}=\underset{P}{inf}\left \{ ||B^{T}PB||^{1/2}:PA+A^{T}P+C^{T}C<0 \right \}$ （inf表示一个集合的最大下界）

可以转化为优化问题：

$min\ \gamma$

$\begin{aligned} s.t.\ &PA+A^{T}P+C^{T}C<0\\ &B^{T}PB\leq \gamma I\\ &P>0 \end{aligned}$

若该问题有一个最优值 $\gamma ^{*}$ ，则 $\Gamma _{ie}=\sqrt{\gamma ^{*}}$ 。该问题是一个具有LMI约束和线性目标函数的凸优化问题，可以用求解器mincx来求全局最优解。

求EP增益定理：如果上述系统是严格真的（D=0）和渐进稳定（A的特征值均有负实部）的，则EP增益有限，且 $\Gamma _{ep}=||CXC^{T}||^{1/2}$ ，矩阵X是以下Lyapunov方程的解：

$AX+XA^{T}+BB^{T}=0$

EP增益也可以由下式确定：

$\Gamma _{ep}=\underset{Q}{inf}\left \{ ||CQC^{T}||^{1/2}:AQ+QA^{T}+BB^{T}<0 \right \}$

可转化为优化问题：

$\begin{aligned} &min\ \gamma\\ s.t.\ &AQ+QA^{T}+BB^{T}<0\\ &CQC^{T}\leq \gamma I\\ &Q>0 \end{aligned}$

若该问题有一个最优值 $\gamma ^{*}$ ，则 $\Gamma _{ep}=\sqrt{\gamma ^{*}}$ 。该问题是一个具有LMI约束和线性目标函数的凸优化问题，可以用求解器mincx来求全局最优解。

求EE增益定理：对上述系统，设 $\gamma >0$ 是一个给定的常数，则以下条件是等价的：

（1）系统渐进稳定，且 $\Gamma _{ee}<\gamma$ ；

（2）存在一个对称矩阵 $P>0$ ，使得

$\begin{bmatrix} A^{T}P+PA &PB &C^{T} \\ B^{T}P & -\gamma I &D^{T} \\ C& D & -\gamma I \end{bmatrix}<0$

矩阵不等式是个线性矩阵不等式，可以用求解器feasp来判断EE增益是否满足给定的约束条件。

求PP增益定理：对上述系统和给定标量 $\gamma$ ，如果存在对称矩阵 $R>0$ ，标量 $\lambda >0$ 和 $\mu >0$ ，使得

$\begin{bmatrix} A^{T}R+RA+\lambda R & RB \\ B^{T}R &-\mu I \end{bmatrix}<0$

$\begin{bmatrix} \lambda R &0 &C^{T} \\ 0 &(\gamma -\mu)I &D^{T} \\ C & D & \gamma I \end{bmatrix}<0$

则 $\Gamma _{pp}<\gamma$ 。上述不等式不是线性矩阵不等式。

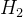$H_{2}$ 性能

传递函数矩阵 $T(s)=C(sI-A)^{-1}B+D$ 的 $H_{2}$ 范数定义为：

$||T(s)||_{2}=Trace(\frac{1}{2\pi }\int_{-\infty }^{+\infty}T(jw)T^{*}(jw)dw)^{1/2}$

$T^{*}(jw)$ 是共轭转置，Trace表示矩阵的迹。T(s)的 $H_{2}$ 范数的平方等于系统脉冲响应的总的输出能量，还等于系统在白噪声输入信号激励下的稳态输出方差。对于单输入单输出系统， $||T(s)||_{2}=\Gamma _{ie}=\Gamma _{ep}$ 。

对于原上述系统，定义矩阵 $X=\int_{0}^{\infty}e^{At}BB^{T}e^{A^{T}t}dt$ （能控格拉姆矩阵）和 $Y=\int_{0}^{\infty}e^{A^{T}t}C^{T}Ce^{At}dt$ （能观格拉姆矩阵），则矩阵X、Y分别满足以下Lyapunova方程：

$AX+XA^{T}+BB^{T}=0$ ； $A^{T}Y+YA+C^{T}C=0$

可得 $||T(s)||_{2}^{2}=Trace(CXC^{T})=Trace(B^{T}YB)$

定理：如果改系统渐进稳定，则有：

（1） $||T(s)||_{2}<\infty$ ，当且仅当D=0；

（2）如果D=0，则 $||T(s)||_{2}<\gamma \Leftrightarrow$

存在对称矩阵X>0，使得 $AX+XA^{T}+BB^{T}<0,\ Trace(CXC^{T})<\gamma ^{2}\Leftrightarrow$

存在对称矩阵Y>0，使得 $A^{T}Y+YA+C^{T}C<0,\ Trace(B^{T}YB)<\gamma ^{2}$

可以用求解器feasp来检验系统是否满足给定的 $H_{2}$ 范数约束条件。

$H_{\infty}$ 性能

T(s)的 $H_{\infty}$ 范数定义为：

$||T(s)||_{\infty}=\underset{w}{sup}\ \sigma _{max}(T(jw))$

即系统频率响应的最大奇异值的峰值。

（奇异值：设 $A\in C^{m\times n}$ ，如果存在非负实数 $\large \sigma$ 和非零向量 $\large u\in C^{n},v\in C^{m}$ 使得

$\large Au=\sigma v,A^{H}v=\sigma u$

则称 $\large \sigma$ 为A的奇异值， $\large u$ 和 $\large v$ 分别为A对应于奇异值 $\large \sigma$ 的右奇异向量和左奇异向量。

$\large A^{H}Au=\sigma ^{2}u,AA^{H}v=\sigma ^{2}v$

$\large \sigma ^{2}$ 是 $\large A^{H}A$ 的特征值，也是 $\large AA^{H}$ 的特征值，而 $\large u$ 和 $\large v$ 分别是 $\large A^{H}A$ 和 $\large AA^{H}$ 对应于特征值 $\large \sigma ^{2}$ 的特征向量。）

$||T(s)||_{\infty}=\Gamma _{ee}$ ，所以可以通过求解以下优化问题：

$\begin{aligned} &min\ \gamma\\ s.t. &\begin{bmatrix} A^{T}P+PA &PB &C^{T} \\ B^{T}P& -\gamma I &D^{T} \\ C&D &-\gamma I \end{bmatrix}<0\\ &P>0 \end{aligned}$

可以得到系统最优 $H_{\infty}$ 性能分析问题的解。该问题是一个具有线性矩阵不等式约束和线性目标凸优化问题，可以用求解器mincx求解。

对离散时间系统：

$\begin{aligned} &x(k+1)=Ax(k)+Bw(k)\\ &z(k)=Cx(k)+Dw(k) \end{aligned}$

求IE增益定理：若系统渐进稳定，则IE增益为 $\Lambda _{ie}=||B^{T}YB+D^{T}D||^{1/2}$ ，其中矩阵Y是以下矩阵方程的解：

$Y=A^{T}YA+C^{T}C$

IE增益也可以由下式得到：

$\Lambda _{ie}=\underset{P}{inf}\left \{ ||B^{T}YB+D^{T}D||^{1/2}:P>A^{T}PA+C^{T}C \right \}$

可以转化为以下优化问题：

$\begin{aligned} &min\ \gamma\\ s.t.\ &A^{T}PA+C^{T}C-P<0\\ &B^{T}PB+D^{T}D\leq \gamma I\\ &P>0 \end{aligned}$

有一个最优值 $\gamma ^{*}$ ，则 $\Lambda _{ie}=\sqrt{\gamma ^{*}}$ 。这是一个具有LMI约束和线性目标函数的凸优化问题，可以用求解器mincx来求全局最优解。

求EP增益定理：若系统渐进稳定，则 $\Lambda _{ep}=||CXC^{T}+DD^{T}||^{1/2}$ ，其中矩阵X是以下Lyapunov方程的解：

$X=AXA^{T}+BB^{T}$

Ep增益也可以由下式得到：

$\Lambda _{ep}=\underset{Q}{inf}\left \{ ||CQC^{T}+DD^{T}||^{1/2}:Q>AQA^{T}+BB^{T} \right \}$

可以转化为以下优化问题：

$\begin{aligned} &min\ \gamma\\ s.t.\ &AQA^{T}+BB^{T}-Q<0\\ &CQC^{T}+DD^{T}\leq \gamma I\\ &Q>0 \end{aligned}$

有一个最优值 $\gamma ^{*}$ ，则 $\Lambda _{ep}=\sqrt{\gamma ^{*}}$ 。这是一个具有LMI约束和线性目标函数的凸优化问题，可以用求解器mincx来求全局最优解。

求EE增益定理：对给定的常数 $\gamma >0$ 和上述离散时间系统，以下条件是等价的：

（1）系统渐进稳定，且EE增益 $\Lambda _{ee}<\gamma$ ；

（2）存在一个对称矩阵P，使得：

$\begin{bmatrix} P &0 \\ 0&\gamma ^{2}I \end{bmatrix}> \begin{bmatrix} A &B \\ C&D \end{bmatrix}^{T} \begin{bmatrix} P &0 \\ 0&I \end{bmatrix} \begin{bmatrix} A &B \\ C&D \end{bmatrix}$

与连续时间系统一样，EE增益也等于系统的 ${\color{Red} H_{\infty}}$ 范数。对给定的标量 $\gamma >0$ ，如果 $||G(z)||_{\infty}<\gamma$ ，则称系统具有 $H_{\infty}$ 性能 $\gamma$ 。

根据Schur补性质，上述（2）中矩阵不等式等价于

$\begin{bmatrix} \begin{bmatrix} -P & 0\\ 0&-\gamma ^{2}I \end{bmatrix} & \begin{bmatrix} A &C \\ B&D \end{bmatrix}^{T}\begin{bmatrix} P &0 \\ 0&I \end{bmatrix}\\ \begin{bmatrix} P &0 \\ 0& I \end{bmatrix}\begin{bmatrix} A &C \\ B&D \end{bmatrix}& \begin{bmatrix} -P &0 \\ 0&-I \end{bmatrix} \end{bmatrix}<0$

这是一个线性矩阵不等式，可以用求解器feasp来判断该线性矩阵不等式的可行性，进而可得系统是否具有 $H_{\infty}$ 性能 $\gamma$ 的结论。通过在此线性矩阵不等式约束下对 $\gamma$ 最小值的搜索，可以得到一个具有线性矩阵不等式约束和线性目标函数得到凸优化问题，因此，可以用求解器mincx来求得该问题的最小值 $\gamma ^{*}$ ，这样一个值称为系统的最优 $H_{\infty}$ 性能指标，正好是系统的EE增益。

第四章控制系统综合

如上图所示的广义系统，其中P(s)是一个线性时不变系统，其状态空间描述为：

$\begin{aligned} &\dot{x}=Ax+B_{1}w+B_{2}u\\ &z=C_{1}x+D_{11}w+D_{12}u\\ &y=C_{2}x+D_{21}w+D_{22}u \end{aligned}$

x、u、y、z分别是状态向量、控制输入、测量输出、被调输出，w是外部扰动（考虑是不确定但具有有限能量的扰动），K(s)是一个控制器的传递函数。

目的：设计一个控制器 $u(s)=K(s)y(s)$ ，使得闭环系统满足：

（1）闭环系统内部稳定，即闭环系统状态矩阵的所有特征值均在左半开复平面

（2）从扰动输入w到被调输出z的闭环传递函数 $T_{wz}(s)$ 的 $H_{\infty}$ 范数小于1，即 $||T_{wz}(s)||_{\infty}<1$ 。

将系统模型中的系数矩阵分别乘以一个适当的常数，可以使闭环系统具有给定的 $H_{\infty}$ 性能 $\gamma$ 。具有给定 $H_{\infty}$ 性能 $\gamma$ 的 $H_{\infty}$ 控制器称为系统的 $\gamma$ -次优控制器。通过对 $\gamma$ 的搜索，可以求取使闭环系统的扰动抑制度 $\gamma$ 最小化的最优 $H_{\infty}$ 控制器（最优 $H_{\infty}$ 控制问题）。

状态反馈 $H_{\infty}$ 控制

状态反馈 $H_{\infty}$ 控制律：假定系统状态可以直接测量得到，静态状态反馈控制器 $u=Kx$ ，使相应的闭环系统 $\begin{aligned} &\dot{x}=(A+B_{2}K)x+B_{1}w\\ &z=(C_{1}+D_{12}K)x+D_{11}w \end{aligned}$ 是渐进稳定的，且闭环传递函数满足 $||T_{wz}(s)||_{\infty}<1$

求状态反馈 $H_{\infty}$ 控制器的定理：对上述系统，存在一个状态反馈 $H_{\infty}$ 控制器，当且仅当存在一个对称正定矩阵X和矩阵W，使得以下矩阵不等式成立：

$\begin{bmatrix} AX+B_{2}W+(AX+B_{2}W)^{T} &B_{1} &(C_{1}X+D_{12}W)^{T} \\ B_{1}^{T}&-I & D_{11}^{T}\\ C_{1}X+D_{12}W&D_{11} &-I \end{bmatrix}<0$

如果上述矩阵不等式存在一个可行解 $X^{*},\ W^{*}$ ，则 $\large u=W^{*}(X^{*})^{-1}x$ 是系统的一个状态反馈 $H_{\infty}$ 控制器。（这是矩阵变量X、W的一个线性矩阵不等式，可以用求解器feasp来求解。此定理给出的是系统所有状态反馈 $H_{\infty}$ 控制律的一个凸约束刻画。）

对给定的标量 $\large \gamma >0$ ，求系统的状态反馈 $\large \gamma$ -次优 $\large H_{\infty}$ 控制器：考虑到

$\large ||T_{wz}(s)||_{\infty}<\gamma \Leftrightarrow ||\gamma ^{-1}T_{wz}(s)||_{\infty}<1$

即可将其转化为标准问题，进一步可转化为以下的求解优化问题：

$\begin{aligned} &min\ \rho \\ s.t.\ &\begin{bmatrix} AX+B_{2}W+(AX+B_{2}W)^{T}&B_{1} &(C_{1}X+D_{12}W)^{T} \\ B_{1}^{T}&-I &D_{11}^{T} \\ C_{1}X+D_{12}W& D_{11} &-\rho I \end{bmatrix}<0\\ &X>0 \end{aligned}$

若该优化问题有解，则该系统的最优 $\large H_{\infty}$ 控制器为 $\large u=W^{*}(X^{*})^{-1}x$ ，相应的最小扰动抑制度为 $\large \sqrt{\rho}$ 。（可用求解器mincx来求解该优化问题。）

输出反馈 $\large H_{\infty}$ 控制

假定：（1） $(A,B_{2},C_{2})$ 是能稳能检测的(对上述线性时不变系统的输出反馈镇定是充分必要的)；（2） $D_{22}=0$ （不失一般性，一般系统的 $H_{\infty}$ 控制问题都可以转化为这一特殊情况）。

目的：设计一个具有以下状态空间实现的输出反馈 $H_{\infty}$ 控制器 $u=K(s)y$ ：

$\begin{aligned} \dot{\hat{x}}=A_{k}\hat{x}+B_{k}y\\ u=C_{k}\hat{x}+D_{k}y \end{aligned}$

其中， $\large \hat{x}\in R^{n_{K}}$ 是控制器的状态， $\large A_{K},B_{K},C_{K},D_{K}$ 是待确定的控制器参数矩阵。

原系统应用该控制器后得到的闭环系统为：

$\begin{aligned} \dot{\xi}=A_{c1}\xi+B_{c1}w\\ z=C_{c1}\xi+D_{c1}w \end{aligned}$

其中：

$\xi=\begin{bmatrix} x\\ \hat{x} \end{bmatrix} , A_{c1}=\begin{bmatrix} A+B_{2}D_{K}C_{2} &B_{2}C_{K} \\ B_{K}C_{2}&A_{K} \end{bmatrix}, B_{c1}=\begin{bmatrix} B_{1}+B_{2}D_{K}D_{21}\\ B_{K}D_{21} \end{bmatrix}$

$C_{c1}=\begin{bmatrix} C_{1}+D_{12}D_{K}C_{2} &D_{12}C_{K} \end{bmatrix}, D_{c1}=D_{11}+D_{12}D_{K}D_{21}$

根据第三章中连续系统的求EE增益定理可知，该控制器是此系统的一个 $H_{\infty}$ 控制器的充要条件为:存在一个对称正定矩阵 $X_{c1}$ ，使得

$\begin{bmatrix} A_{c1}^{T}X_{c1}+X_{c1}A_{c1} &X_{c1}B_{c1} &C_{c1}^{T} \\ B_{c1}^{T}X_{c1}&-I &D_{c1}^{T} \\ C_{c1}&D_{c1} &-I \end{bmatrix}<0$

此矩阵不等式中，矩阵变量 $X_{c1}$ 与控制器参数矩阵 $A_{K},B_{K},C_{K},D_{K}$ 以非线性的方式出现，难以直接处理求解，采用下面两种基于线性矩阵不等式处理的输出反馈 $H_{\infty}$ 控制器设计方法——消元法和变量替代法。

消元法：（此处省略推导过程，直接给出结论定理）。

定理：原线性定常系统存在一个输出反馈 $H_{\infty}$ 控制器，当且仅当存在对称正定矩阵X和Y，使得

$(a).\quad \begin{bmatrix} N_{o} &0 \\ 0&I \end{bmatrix}^{T} \begin{bmatrix} A^{T}X+XA&XB_{1} &C_{1}^{T} \\ B_{1}^{T}X&-I &D_{11}^{T} \\ C_{1}&D_{11} &-I \end{bmatrix} \begin{bmatrix} N_{o} &0 \\ 0&I \end{bmatrix} <0$

$(b).\quad \begin{bmatrix} N_{c} &0 \\ 0&I \end{bmatrix}^{T} \begin{bmatrix} AY+YA^{T}&YC_{1}^{T} &B_{1} \\ C_{1}Y&-I &D_{11} \\ B_{1}^{T}&D_{11}^{T} &-I \end{bmatrix} \begin{bmatrix} N_{c} &0 \\ 0&I \end{bmatrix} <0$

$(c).\quad \begin{bmatrix} X &I \\ I&Y \end{bmatrix}\geq 0$

其中 $N_{o}$ 和 $N_{c}$ 分别是以子空间 $ker([C_{2}\ \ D_{21}])$ 和 $ker([B_{2}^{T}\ \ D_{12}^{T}])$ 中的任意一组基向量作为列向量所构成的矩阵。可以用求解器feasp来求解。若核空间中有等于零空间，则相应的 $N_{o}$ 或 $N_{c}$ 取为 $I$ 。

设计步骤：

1. 求解满足上述定理条件的矩阵X和Y。

2. 求满足 $\large X-Y^{-1}=X_{2}X_{2}^{T}$ 的矩阵 $\large X_{2}\in R^{n\times n_{k}}$ ，其中的 $\large n_{k}$ 可以选成是矩阵 $\large X-Y^{-1}$ 的秩。可以采用奇异值分解的方法得到这样的矩阵 $\large X_{2}$ 。用矩阵 $\large X$ 和 $\large X_{2}$ 构造 $\large X_{c1}=\begin{bmatrix} X &X_{2}^{T} \\ X_{2}&I \end{bmatrix}$

3. 将得到的矩阵 $\large X_{c1}$ 代入到矩阵不等式 $\large H_{X_{c1}}+P_{X_{c1}}^{T}KQ+Q^{T}K^{T}P_{X_{c1}}<0$ 中，得到只包含矩阵 $\large K$ 的线性矩阵不等式，从而求出 $\large H_{\infty}$ 控制器的参数矩阵 $\large K$ 。

注：3中矩阵不等式满足：

$H_{X_{c1}}= \begin{bmatrix} A_{0}^{T}X_{c1}+X_{c1}A_{0} &X_{c1}B_{0} &C_{0}^{T} \\ B_{0}^{T}X_{c1}&-I &D_{11}^{T} \\ C_{0}&D_{11} &-I \end{bmatrix}\\ P_{X_{c1}}=\begin{bmatrix} \bar{B}^{T}X_{c1} &0 &\bar{D}_{12}^{T} \end{bmatrix},\quad\quad Q=\begin{bmatrix} \bar{C} &\bar{D}_{21} &0 \end{bmatrix}$

$A_{0}=\begin{bmatrix} A&0 \\ 0&0 \end{bmatrix},\ B_{0}=\begin{bmatrix} B_{1} \\ 0 \end{bmatrix},\ C_{0}=\begin{bmatrix} C_{1}&0 \end{bmatrix}\\ \bar{B}=\begin{bmatrix} 0&B_{2} \\ I&0 \end{bmatrix},\ \bar{C}=\begin{bmatrix} 0&I \\ C_{2}&0 \end{bmatrix},\ \bar{D}_{12}=\begin{bmatrix} 0 &D_{12} \end{bmatrix},\ \bar{D}_{21}=\begin{bmatrix} 0 \\ D_{21} \end{bmatrix}$

输出反馈 $\gamma -$ 次优 $H_{\infty}$ 控制器：将上述定理中不等式(a)和(b)左边中间矩阵里的 $-I$ 项改为 $-\gamma I$ 再求解。

进一步得输出反馈最优 $H_{\infty}$ 控制器可以通过求解以下优化问题得到：

$\begin{aligned} &min\ \rho\\ s.t.\ &\begin{bmatrix} N_{o} &0 \\ 0&I \end{bmatrix}^{T} \begin{bmatrix} A^{T}X+XA&XB_{1} &C_{1}^{T} \\ B_{1}^{T}X&-\rho I &D_{11}^{T} \\ C_{1}&D_{11} &-\rho I \end{bmatrix} \begin{bmatrix} N_{o} &0 \\ 0&I \end{bmatrix} <0\\ &\begin{bmatrix} N_{c} &0 \\ 0&I \end{bmatrix}^{T} \begin{bmatrix} AY+YA^{T}&YC_{1}^{T} &B_{1} \\ C_{1}Y&-\rho I &D_{11} \\ B_{1}^{T}&D_{11}^{T} &-\rho I \end{bmatrix} \begin{bmatrix} N_{c} &0 \\ 0&I \end{bmatrix} <0\\ &\begin{bmatrix} X &I \\ I&Y \end{bmatrix}\geq 0 \end{aligned}$

可通过求解器mincx进行求解。

连续时间系统 $H_{\infty}$ 控制器综合问题求解器hinflmi()（离散系统是dhinflmi()）:

先用ltisys函数建立系统，G=ltisys(A,B,C,D) ，再使用hinflmi()函数即可得到最优 $H_{\infty}$ 控制器。hinflmi函数的基本用法是 [gopt,K]=hinflmi(system,[p m],n)，其中p是系统测量输出的个数，m是系统控制输入的个数，n表示性能指标范围即 $\gamma <n$ ，这个函数通过mincx来优化系统的 $H_{\infty}$ 性能指标，gopt是性能指标，K是最优 $H_{\infty}$ 控制器的系统矩阵，可通过ltiss()函数得到其状态空间实现，即[Ak,Bk,Ck,Dk]=ltiss(K)，还可以通过[g,K,x1,x2,y1,y2]=hinflmi(G,[p,m],n)得到解矩阵X=x1和Y=y1。
clsys=slft(G,K)得到闭环系统，spol(clsys)根据闭环极点检验闭环系统稳定性，norminf(clsys)得到外部扰动w到被调输出z的闭环系统增益。

$\large H_{2}$ 控制

考虑状态空间模型： $\begin{aligned} \dot{x}& =Ax+B_{1}w+B_{2}u\\ z&=Cx+Du \end{aligned}$ ，给定标量 $\gamma >0$ ，设计一个状态反馈控制律 $u=Kx$ ，使得闭环系统 $\begin{aligned} \dot{x}& =(A+B_{2}K)x+B_{1}w\\ z&=(C+DK)x \end{aligned}$ 是渐进稳定的，并且闭环传递函数 $T_{wz}(s)$ 的 $H_{2}$ 范数满足 $||T_{wz}(s)||_{2}<\gamma$ ，此控制律称为系统的一个状态反馈控制律。

定理：对给定标量 $\gamma >0$ ，系统存在状态反馈 $H_{2}$ 控制律，当且仅当存在对称正定矩阵 $X$ 、 $Z$ 和矩阵 $W$ ，使得

$\begin{aligned} AX+B_{2}W+(AX+B_{2}W)^{T}+B_{1}B_{1}^{T}&<0\\ \begin{bmatrix} -Z&CX+DW \\ (CX+DW)^{T}& -X \end{bmatrix}&<0\\ Trace(Z)&<\gamma ^{2} \end{aligned}$

如果上述LMI存在可行解 $X^{*},W^{*},Z^{*}$ ，则 $u=W^{*}(X^{*})^{-1}x$ 是系统的一个状态反馈 $H_{2}$ 控制律。可用求解器feasp求解。

进一步可得求解系统最优状态反馈 $H_{2}$ 控制律的设计方法为：求解以下带LMI约束的线性目标函数的凸优化问题，可用求解器mincx求解。

$\begin{aligned} &min \rho\\ s.t.\ \ &AX+B_{2}W+(AX+B_{2}W)^{T}+B_{1}B_{1}^{T}<0\\ &\begin{bmatrix} -Z&CX+DW \\ (CX+DW)^{T}& -X \end{bmatrix}<0\\ &Trace(Z)<\rho \end{aligned}$

$H_{2}/H_{\infty}$ 控制

在实际设计问题中，人们通常需要所设计的系统满足多种性能要求。特别地，对于系统：

$\begin{aligned} &\dot{x}=Ax+Bu+B_{1}w_{1}+B_{2}w_{2}\\ &z_{1}=C_{1}x+D_{10}u+D_{11}w_{1}\\ &z_{2}=C_{2}x+D_{20}u+D_{22}w_{2} \end{aligned}$

设计一个控制器，使得闭环系统渐进稳定，且从 $w_{1}$ 到 $z_{1}$ 的闭环传递函数 $T_{w_{1}z_{1}}$ 的 $H_{\infty}$ 范数不超过一个给定的上界 $\gamma _{1}$ ，以保证闭环系统对由 $w_{1}=\Delta z_{1}$ 进入的不确定性具有鲁棒稳定性；同时使得从 $w_{2}$ 到 $z_{2}$ 的闭环传递函数 $T_{w_{2}z_{2}}$ 的 $H_{2}$ 范数尽可能小，以保证用 $H_{2}$ 范数度量的系统性能处于一个好的水平。即使得闭环系统满足

$\sigma (A_{c})\in C^{-},\ ||T_{w_{1}z_{1}}||_{\infty}<\gamma _{1},\ ||T_{w_{2}z_{2}}||_{2}<\gamma _{2}$

的所有控制器中，寻找使得 $\gamma _{2}$ 最小化的控制器，称为系统的多目标 $H_{2}/H_{\infty}$ 控制问题，或简称为 $H_{2}/H_{\infty}$ 控制问题。通过对不同标量 $\gamma _{1}$ 求解相应的 $H_{2}/H_{\infty}$ 控制问题，可以分析系统 $H_{2}$ 性能和 $H_{\infty}$ 性能之间的关系，如通过牺牲系统的鲁棒性可以在多大程度上改进系统的性能。

控制律设计：

在状态反馈 $u=Kx$ 下，闭环系统为：

$\begin{aligned} &\dot{x}=(A+BK)x+B_{1}w_{1}+B_{2}w_{2}\\ &z_{1}=(C_{1}+D_{10}K)x+D_{11}w_{1}\\ &z_{2}=(C_{2}+D_{20}K)x+D_{22}w_{2} \end{aligned}$

对原系统和一个给定的标量 $\gamma _{1}>0$ ，若 $D_{22}=0$ ，且以下优化问题

$\begin{aligned} &min\ \gamma _{2}\\ s.t.\ &\begin{bmatrix} AX+BW+(AX+BW)^{T}& B_{1} &(C_{1}X+D_{10}W)^{T} \\ B_{1}^{T}&-\gamma _{1}I &D_{11}^{T} \\ C_{1}X+D_{10}W & D_{11} & -\gamma _{1}I \end{bmatrix}<0\\ &AX+BW+(AX+BW)^{T}+B_{2}B_{2}^{T}<0\\ &\begin{bmatrix} -Z &C_{2}X+D_{20}W \\ (C_{2}X+D_{20}W)^{T}&-X \end{bmatrix}<0\\ &Trace(Z)<\gamma _{2} \end{aligned}$

有一个最优解 $X^{*},\ W^{*}$ ，则原系统的状态反馈 $H_{2}/H_{\infty}$ 控制问题是可解的，且 $u=W^{*}(X^{*})^{-1}x$ 是系统的一个状态反馈 $H_{2}/H_{\infty}$ 控制律。这是一个具有LMI约束和线性目标函数的凸优化问题，可以用求解器mincx来求解。

hinfmix函数：

LMI工具箱提供了求解 $H_{2}/H_{\infty}$ 控制问题的一个函数hinfmix，该函数求解了由下图所示的多目标输出反馈控制问题。

$T_{\infty}(s)$ 和 $T_{2}(s)$ 作为从 $w$ 到 $z_{\infty}$ 和从 $w$ 到 $z_{2}$ 的闭环传递函数，则hinfmix可以计算以下综合问题的解。

设计一个线性时不变控制器 $K(s)$ ，使闭环系统满足：

$||T_{\infty}||_{\infty}<\gamma _{0},\quad ||T_{2}||_{2}<\nu _{0},\quad$ 闭环系统极点位于某个给定的LMI区域D且使得性能指标 $\alpha ||T_{\infty}||_{\infty}^{2}+\beta ||T_{2}||_{2}^{2}$ 最小化。

函数hinfmix的一般形式为：[gopt, h2opt, K, R, S]=hinfmix(P, r, obj, region, dkbnd, tol)

(输入项中，P是控制对象P(s)的系统矩阵表示，r是一个3元向量，依次表示了 $z_{2}$ 、 $y$ 和 $u$ 的维数。 $z_{\infty}$ 和 $z_{2}$ 可以是空的。obj是一个4元向量，表示了 $H_{2}/H_{\infty}$ 约束及性能指标中的 $H_{\infty}$ 性能和 $H_{2}$ 性能的权重情况， $obj=\begin{bmatrix} \gamma _{0} &\nu _{0} &\alpha &\beta \end{bmatrix}$ 。输入项中的其余部分是可选择的。)