一、滤波器设计
二、多速率处理
将一个信号从某一给定的采样速率转换到另一个不同采样率的过程称为采样率转换。

1. 整数倍抽样
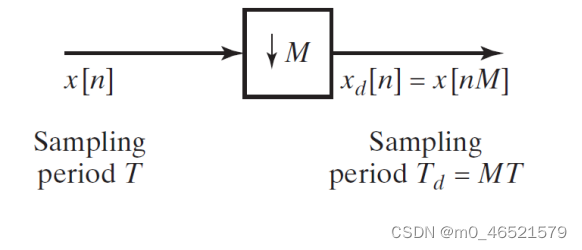
的离散时间傅里叶变换(DTFT):
整数倍抽样后:
即:
的离散时间傅里叶变换(DTFT):
令,其中
则
整数倍抽样后的数字信号的离散时间傅里叶变换
可以看作是由频率受到
倍扩展的,并按
的整数倍移位的
个周期傅里叶变换
复本的幅度加权和。
连续时间信号

采样信号

离散时间信号

整数倍抽样后信号,
, 令
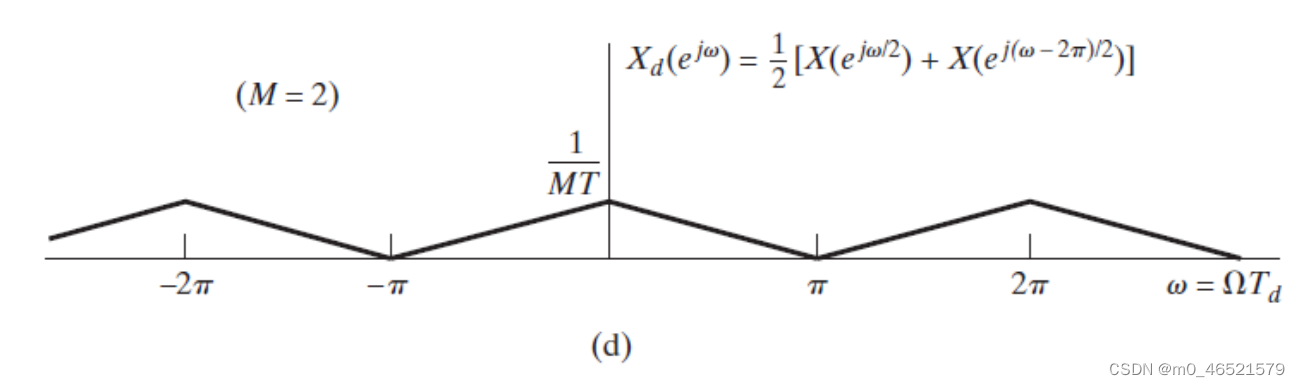
对应的采样信号

若,
,且
,则抽样后不会产生混叠。
若M选取不合理,会导致混叠抽样,故一般在抽样前会加预滤波避免混叠。

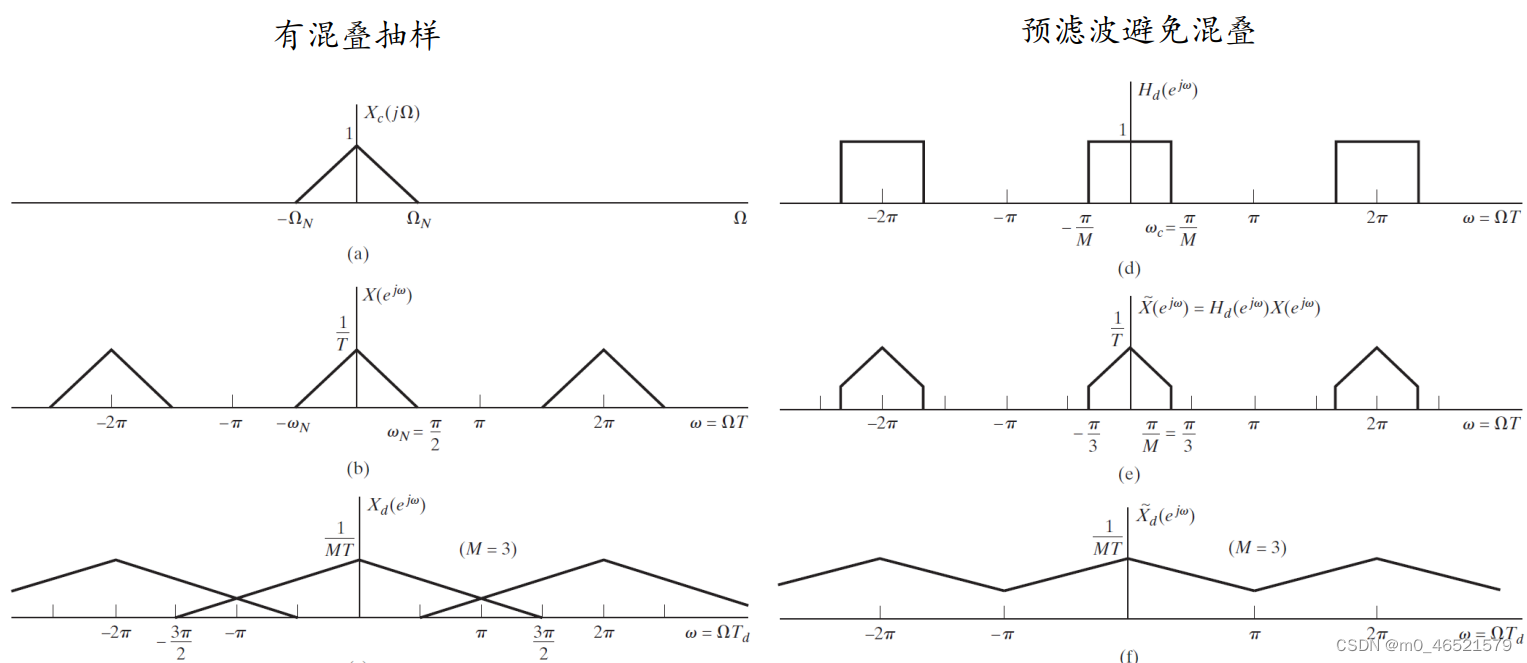
2. 整数倍插值


插值后的序列
但是无法实现,可采用简单线性插值









 本文详细探讨了整数倍抽样与插值技术,在信号处理中,整数倍抽样涉及将信号从一个采样率转换到另一个采样率。文章解释了整数倍抽样的离散时间傅里叶变换(DTFT)特性,以及如何通过预滤波避免混叠现象。同时介绍了整数倍插值的基本原理。
本文详细探讨了整数倍抽样与插值技术,在信号处理中,整数倍抽样涉及将信号从一个采样率转换到另一个采样率。文章解释了整数倍抽样的离散时间傅里叶变换(DTFT)特性,以及如何通过预滤波避免混叠现象。同时介绍了整数倍插值的基本原理。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








