参考书籍:
Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, Second Edition;
机器学习 周志华
编译器:jupyter notebook
本文章涉及到的西瓜书中的公式不做推导和说明
4.1 线性回归
最终的多元线性回归方程是:
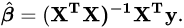
接下来用θ代替图中的β(没找到θ的图)
生成一组线性数据测试这个公式
import numpy as np
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)
我们生成的这组数据就是一个类 y = 3 x + 4 (0 < x < 2)的分布点集
np.random后面可以接.rand(),.randn(),.randint()等形式,他们的用法详见这里
我们用最开始的标准方程来计算θ
np.linalg中的inv()函数对矩阵求逆,并用dot()计算矩阵的内积
#np.c_按行合并;np.ones生成100*1的1数组
X_b = np.c_[np.ones((100, 1)),X]
#计算标准方程(XTX)-1XTy
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best
输出:
array([[4.44082239],
[3.02945868]])
上述函数详见:
Python numpy函数:zeros()、ones()、empty()
numpy 学习之 np.c_的用法
现在用之前所求的θ做出两边端点预测
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)), X_new]
y_predict = X_new_b.dot(theta_best)
y_predict
输出:
array([[ 4.44082239],
[10.49973976]])
由于这里应用线性回归,预测结果必为直线。这里所求得的预测结果就是二元平面上的直线,所以根据之前求得的两边端点(0,2)的预测就可以绘制直线
绘制模型的预测结果:
import matplotlib.pyplot as plt
plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()

上面我们用了最淳朴的方式计算了一遍线性回归,而sklearn中有线性回归的运算函数
#Scikit-Learn实现上述代码
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
输出:
(array([4.44082239]), array([[3.02945868]]))
根据这篇文章:sklearn中的coef_和intercept_,我们大概能推断出,线性预测公式f(x)=wx+b中,.intercept_是b,.coef_是w
这时,我们也大概可以理解之前X_b中应用函数ones的意义,那种方法没有.intercept_和.coef_的区分,第一列1与b相乘,之后的每列x与相应的w相乘,b作为w[0],最终得到一个最终全部结果的行矩阵(即theta_best)
或者我们有一种更简单的方式求出theta_best
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd
输出:
array([[4.44082239],
[3.02945868]])
这个函数是计算(X+)y(这里的X+为X的伪逆),但是可以用np.linalg.pinv()直接计算出伪逆
np.linalg.pinv(X_b).dot(y)
输出:
array([[4.44082239],
[3.02945868]])
这样,我们就有四种方法可以求出预测的函数值了
4.2 梯度下降
理论部分详见书籍or资料
4.2.1 批量梯度下降
公式:θ(下一步)=θ-η▽θMSE(θ)
看一下这个公式的快速实现
#批量梯度下降
eta = 0.1
n_iterations = 1000
m = 100
theta = np.random.randn(2,1)
#randn是正态分布
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
theta
输出:
array([[4.44082239],
[3.02945868]])
我们发现这个数据和之前我们那四种方法求得的数据一模一样,表现得十分完美,而其中功不可没的是,我们设置了一个合适的eta(η 学习率)值
想要找到合适的学习率,可以使用网格搜索,在此不做过多叙述
4.2.2 随机梯度下降
随机梯度下降的优势是,可以跳出局部最小值,但缺陷也很明显,永远找不到最小值,他的原理是,每次都随机找到一个样本点进行数据的下一步的调整
我们用50次遍历就可以得到一个很好方案(而上面用了1000次)
#随机梯度下降
n_epochs = 50
t0, t1 =5, 50
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1)
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
#randint:0-m之间的整数
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m +i)
theta = theta -eta * gradients
theta
输出:
array([[4.426646 ],
[3.04030804]])
而随机梯度下降可以sklearn简单表示
#Scikit-Learn实现上述代码
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
(array([4.43004106]), array([3.05933965]))
4.3 多项式回归
当数据比直线更复杂的时候,我们就要用到多项式回归
我们生成一组新的数据
import numpy as np
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.rand(m, 1)
这是一个类y = 1/2 X*X + X + 2 (-3 < x < 3)的分布点集,我们来看一下
import matplotlib.pyplot as plt
plt.plot(X, y, 'b.')
plt.show()

因此,一条直线永远无法正确拟合此数据,我们用PolynomialFeatures 类来转换训练数据,将每个特征的平方(degree = 2)来作为新特征
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
输出:
array([2.41278383])
X_poly[0] #X[0]的原始特征以及该特征的平方
输出:
array([2.41278383, 5.82152582])
X_poly[0]现在包含X的原始特征和该特征的平方,现在将LinearRegression 模型拟合到此训练数据中
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y, sample_weight=2)
lin_reg.intercept_, lin_reg.coef_ #b && theta
输出:
(array([2.50160549]), array([[1.00300224, 0.49453891]]))
我们来画一下这个预测的图像
注:1.这步是我另写,一直predict不过,后来我到sklearn的官网查到 LinearRegression 的 fit() 函数有一个参数是 sample_weight 代表有几个特征(默认=None),所以我在上面的 fit 中添加了这个参数,才可以进行 predict
2.画图的原理是相邻的两个点之前进行一个连线,所以我用backup储存了X数据并进行排序(axis=0为按二维中的列排序),并且用之前的方法重新平方,即可以根据之前的方法进行预测
backup = X
backup = np.sort(backup,axis=0)
X_sorted_poly = poly_features.fit_transform(backup)
y_sorted_pred = lin_reg.predict(X_sorted_poly)
plt.plot(backup, y_sorted_pred, 'r-')
plt.plot(X, y, 'b.')
plt.show()

4.4 学习曲线
学习曲线:除了交叉验证另一种区别模型过于简单or复杂的方法
是训练集和验证集上关于训练集大小的性能函数,横坐标为训练集大小,纵坐标为RMSE(root mean square error 均方根误差)
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
train_errors, val_errors= [], []
for m in range(1,len(X_train)):
model.fit(X_train[:m],y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
return X_train, X_val, y_train, y_val
lin_reg = LinearRegression()
X_train, X_val, y_train, y_val = plot_learning_curves(lin_reg, X, y)
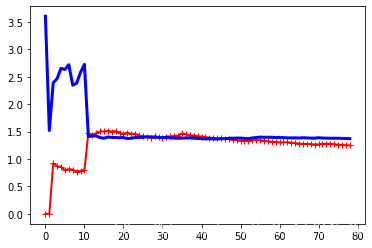
我们可以看到,最开始只有一两个实例时,模型可以很好的拟合,所以RSME时0,数据越多,模型就不可能完美的拟合训练数据,因为数据既有噪声,又不是线性的。因此训练数据上的误差会一直上升,直到达到平衡状态。
上面这种曲线时欠拟合模型,两条曲线都达到了平稳状态,很接近且很高。
解决方案:增加训练阶数
过拟合:训练数据的误差较低,但是曲线之间存在缝隙。
解决方案:使用更大的训练集
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_fetures", PolynomialFeatures(degree=4, include_bias=False)),
("lin_reg", LinearRegression()),
])
X_train, X_val, y_train, y_val = plot_learning_curves(polynomial_regression, X, y)
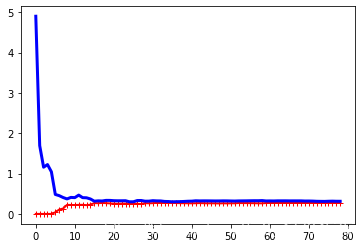
4.5 正则化线性模型
一切的一切都是为了防止过拟合。
正则化是通过约束模型的权重来实现的
4.5.1 岭回归(Tikhonov正则化)
岭回归
#岭回归
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
array([[5.5626674]])
并采用随机梯度下降法
#随机梯度下降
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(penalty="l2")
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
array([5.55077116])
4.5.2 Lasso回归
#Lasso回归
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
#等同于lasso_reg = SGDRegressor(penalty="l1")
lasso_reg.fit(X, y.ravel())
lasso_reg.predict([[1.5]])
array([5.52508037])
4.5.3 弹性网络
#弹性网络:结合Lasso和岭回归,是Lasso的改进模式
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
array([5.52104439])
4.5.4 提前停止法
一轮一轮的训练之后,最开始RMSE是在下降,但轮次达到一定数量之后会上升,就是过拟合的体现。所以我们规定在误差值达到最小时就停止训练。
#提前停止法
from sklearn.base import clone
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
#prepare the data
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler())
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sge_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train.ravel())
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = clone(sgd_reg)
4.6 逻辑回归
4.6.1 决策边界
我们用一个新的数据集:150朵三个品种的花
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
输出:
['data',
'target',
'frame',
'target_names',
'DESCR',
'feature_names',
'filename']
我们只用花瓣宽度这一个特征,创建一个分类器,仅检验是否是“2”号花
import numpy as np
X = iris["data"][:,3:]
y = (iris["target"] == 2).astype(np.int)
训练一个逻辑回归模型
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)
我们看看0-3cm之前的花,模型估算出的概率是多少
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
import matplotlib.pyplot as plt
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris virginica")

估算一下1.7和1.5分类器预测它是否是"2"号花
log_reg.predict([[1.7], [1.5]])
array([1, 0])
分别是"是"和"不是"
4.6.2 Softmax回归
我们用softmax回归将花分为三类, 当用两个以上的类进行训练时, LogisticRegression是一种很好的一对多方式, multi_class=“multinomial” 就可以切换成超参数回归
X = iris["data"][:,(2,3)]
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs",C=10)
softmax_reg.fit(X, y)
预测一下花瓣长5cm宽2cm的种类
softmax_reg.predict([[5,2]])
array([2])
观察一下每种花的预测分数
softmax_reg.predict_proba([[5,2]])
array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








