2021-06-17

用于学生成绩预测的基于图的习题和知识感知学习网络

提出背景

现有的预测学生成绩的方法：要么利用教育心理学方法根据所学习的知识熟练程度来预测学生的成绩，要么充分利用协同过滤模型来表示学生和练习的潜在因素。
然而，这些方法中的大多数要么忽略了特定于习题的特征(例如，习题材料)，要么不能充分探索学生、习题以及知识概念之间的高阶交互作用。
为此，我们提出了一个基于图形的习题和知识感知学习网络，用于准确的预测学生成绩。具体来说，我们分别学习学生对习题和知识概念的掌握，以模拟习题和知识概念的双重效果。然后，为了模拟高阶相互作用，我们在预测过程中应用图形卷积技术。

提出的模型（Graph-EKLN）

问题定义

假设有$M$个学生，$N$个习题，$O$个知识概念。学生和练习之间的互动用矩阵 R = { r s p } M × N R = \{ r_{sp} \}_{M×N} R={rsp​}M×N​表示，其中$r_{sp}$表示学生s在练习p上的成绩(0/1)。用矩阵 Q = { q p k } N × O Q = \{ q_{pk} \}_{N×O} Q={qpk​}N×O​表示习题与知识概念相关联关系，其中如果习题$p$与知识概念$k$有关，则$q_{pk}=1$，如果它们之间没有关系，则$q_{pk}=0$。
给定$R$和$Q$，我们旨在预测未观察到的${\hat{r}}_{sp}$，即学生$s$未作答过的习题。

模型框架图

在图的左边部分，根据矩阵$R$建立学生与习题的联系，根据矩阵$Q$建立习题与知识概念的联系。
任务中存在两个挑战：如何处理学生和习题之间的不同链接(正确答案/错误答案)，以及如何在基于MF的模型中利用知识概念信息。
为了解决这两个挑战，我们将任务分成两个子任务，如图2的中间部分所示。
第一个子任务是预测学生$s$对习题$p$本身的熟练程度${\hat{r}}_{sp}^P$，第二个子任务是预测学生$s$对习题相关知识概念的熟练程度${\hat{r}}_{sp}^K$。

高阶协同信息建模(针对挑战1)

在习题空间中，学生嵌入和习题嵌入分别为$U=[u_1,..,u_s,...,u_M]\in R^{M\times D}$，$V=[v_1,...,v_p,...,v_N]\in R^{N\times D}$。为了解决提到的不同链接问题，我们遵循R-GCN (它主要学习多关系图的表示）。

上图概述了模型中的单层GCN传播过程。具体来说，我们利用基于多层感知器(MLPs)的链接特定的聚合函数用于两种链接，从而获得高阶学生和习题的嵌入。

1. 学生和练习的初始嵌入可以表述为$h_s^0=u_s$，$h_p^0=v_p$
2. 假设有L个传播层。学生在第(L+1)层的嵌入可以表述为:
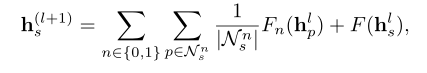
   其中$N_s^n$表示学生的第n类邻居，即学生回答正确和错误的习题。使用三种类型的函数$F、F_0、F_1$来区分学生的邻居的聚合过程以及学生自身与MLPs的聚合过程。习题$p$的嵌入可以通过以同样的方式聚合其邻居节点的嵌入来获得。
3. 传播信息后，我们可以获得$[h_s^0，...，h_s^l，..，h_s^L]$和$[h_p^0，...,h_p^l，..，h_p^L]$作为学生和习题在每一层的嵌入。我们将每一层的嵌入连接如下:
   其中$||$操作为：将新向量拼接到原来的向量之后，对应着维数增加。
4. 通过计算串联嵌入的内点，可以得到学生在习题空间中对习题p的熟练程度：${\hat{r}}_{sp}^P=h_s^T{h}_p$

知识概念的信息建模（针对挑战2）

在知识概念空间中，$X=[x_1，...，x_s，...，x_M]\in R^{M\times D}$ 和 $Y=[y_1，...，y_k，...，Y_O]\in R^{O\times D}$分别表示学生和知识概念的表示。然后，我们用内积来预测${\hat{r}}_{sp}^K$:

其中$|K_p|$表示与习题$p$相关的知识概念集。

请注意，我们这里不使用GCN层。事实上，知识概念的数量比练习的数量少得多。因此，学生和知识概念之间的关系不够稀疏。因此，我们保留它们的原始嵌入，而不使用GCN层避免过度平滑。

性能预测

预测函数定义为:${\hat{r}}_{sp}={\hat{r}}_{sp}^P+\alpha {\hat{r}}_{sp}^K$
其中α是用于控制两个子任务之间平衡的超参数。
损失函数：

其中$T$表示训练数据中$(s，p，r_{sp})$三元组的数量。