数据结构与算法(十六)——二叉排序树、平衡二叉树、多叉树

最新推荐文章于 2023-04-10 21:44:02 发布
最新推荐文章于 2023-04-10 21:44:02 发布
阅读量429 收藏
点赞数
分类专栏： 数据结构 文章标签： b树 数据结构 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_48468380/article/details/124474127
版权

二叉排序树(BST)

二叉排序树：BST(Binary Sort(Search) Tree)，对于BST中任何一个非叶子结点，要求左子节点的值比当前结点的值小，右子节点的值比当前结点的值大。对于相同的值，可以将该结点放在左子节点或者右子节点

代码实现

  1. 添加结点：根据结点的值，将值小的结点放在左边，值大的结点放在右边
  2. 遍历结点：与一般树的前中后序遍历无异
  3. 删除结点：
  1. 删除叶子结点：找到需要删除的结点的父结点，然后将叶子结点置空
  2. 删除只有一个子结点的结点：找到需要删除的结点的父结点，将父结点的子结点位置改成子的子，即用子结点替换掉需要删除的节点
  3. 删除有两个子结点的结点：找到需要删除的结点的父结点，找到右子树的最左(小)结点、或左子树最右(大)结点替代需要删除的结点
/***
 * 二叉排序树
 * 
 * @author laowa
 *
 */
class BinarySortTree {

	Node root;

	/**
	 * 添加结点
	 * 
	 * @param node
	 */
	public void add(Node node) {
		if (root == null) {
			root = node;
			return;
		}
		root.add(node);
	}

	/**
	 * 删除结点
	 * 
	 * @param no
	 *            需要删除的结点的no
	 */
	public void delete(int no) {
		// 判空
		if (this.root == null) {
			System.out.println("树为空");
			return;
		}
		// 找到目标节点和目标节点的父结点
		Node target = this.search(no);
		// 如果没有找到目标结点直接退出方法
		if (target == null) {
			return;
		}
		Node parent = this.root.searchParent(no);

		// 如果该树只有一颗结点，则直接根结点置空
		if (root.left == null && root.right == null) {
			this.root = null;
			return;
		}

		if (target.left == null && target.right == null) {
			// 如果左右子结点均为空，表示当前结点为叶子结点
			// 找到目标结点在父结点的左边还是右边，然后置空
			if (parent.left == target) {
				parent.left = null;
			} else {
				parent.right = null;
			}
			return;
		}

		// 如果左子结点为空,说明只有一棵右子树
		if (target.left == null) {
			if (parent == null) {
				// 如果父结点为空，即删除的结点是根结点
				this.root = target.right;
			} else {
				// 找到目标结点在父结点的左边还是右边，然后指向目标结点的右边
				if (parent.left == target) {
					parent.left = target.right;
				} else {
					parent.right = target.right;
				}
			}

		}

		// 如果右子结点为空，说明只有一棵左子树
		if (target.right == null) {
			if (parent == null) {
				// 如果父结点为空，即删除的结点是根节点
				this.root = target.left;
			} else {
				// 找到目标结点在父结点的左边还是右边，然后指向目标结点的左边
				if (parent.left == target) {
					parent.left = target.left;
				} else {
					parent.right = target.left;
				}
			}

		}

		if (target.left != null && target.right != null) {
			// 如果目标结点的左右子结点均不为空
			Node temp = target.right;
			// 向左循环查找一直找到最左边的结点，此时temp保存了这个结点
			while (temp.left != null) {
				temp = temp.left;
			}
			// 删除该结点
			delete(temp.no);
			// 将目标结点的左右子结点赋值给该结点
			temp.left = target.left;
			temp.right = target.right;
			// 如果parent为空表示删除的结点是根节点，没有父结点，否则找到目标结点在父结点的左边还是右边，并且设置为temp结点
			if (parent != null) {
				if (parent.left == target) {
					parent.left = temp;
				} else {
					parent.right = temp;
				}
			} else {
				this.root = temp;
			}

		}

	}

	/**
	 * 查找目标结点
	 * 
	 * @param no
	 *            目标结点的编号
	 * @return 结点
	 */
	public Node search(int no) {
		if (this.root == null) {
			return null;
		}
		return this.root.search(no);
	}

	/**
	 * 中序遍历
	 */
	public void infixOrder() {
		if (root == null) {
			System.out.println("树为空");
			return;
		}
		root.infixOrder();
	}
}

/***
 * 二叉排序树结点
 * 
 * @author laowa
 *
 */
class Node {
	int no;
	Node left;
	Node right;

	public Node(int no) {
		this.no = no;
	}

	@Override
	public String toString() {
		return "[Node value=" + no + "]";
	}

	/**
	 * 查找当前需要删除的结点
	 * 
	 * @param no
	 *            结点编号
	 */
	public Node search(int no) {
		if (this.no == no) {
			// 如果当前结点为需要查找的结点，返回
			return this;
		}
		if (this.no > no) {
			// 如果目标编号小于当前结点，表示目标结点在左边
			if (this.left != null) {
				return this.left.search(no);
			}
			// 没找到
			return null;
		}
		// 如果目标编号大于当前结点，表示目标结点在右边
		if (this.right != null) {
			return this.right.search(no);
		}
		// 没找到
		return null;
	}

	/**
	 * 查找需要删除的结点的父结点
	 * 
	 * @param no
	 * @return
	 */
	public Node searchParent(int no) {
		// 如果作右子结点中存在目标结点，则放回当前结点
		if ((this.left != null && this.left.no == no) || (this.right != null && this.right.no == no)) {
			return this;
		}
		// 如果当前结点大于目标结点，向左递归查找
		if (this.no > no && this.left != null) {
			return this.left.searchParent(no);
		}
		// 如果当前结点小于目标结点，向右递归查找
		if (this.no < no && this.right != null) {
			return this.right.searchParent(no);
		}
		// 没找到返回null
		return null;
	}

	/**
	 * 添加结点
	 * 
	 * @param node
	 *            待添加的结点
	 */
	public void add(Node node) {
		// 判空，添加的结点为空则不添加
		if (node == null) {
			return;
		}
		if (node.no < this.no) {
			// 如果待添加的结点小于当前节点，想左子树添加
			if (this.left == null) {
				// 如果左子节点为空则直接加载左边
				this.left = node;
			} else {
				// 否则向左子结点递归添加
				this.left.add(node);
			}
		} else {
			// 如果待添加的结点大于或等于当前结点，向右子树添加
			if (this.right == null) {
				// 如果右子节点为空则直接加在右边
				this.right = node;
			} else {
				// 否则向右子结点递归添加
				this.right.add(node);
			}
		}
	}

	/**
	 * 中序遍历
	 */
	public void infixOrder() {
		if (this.left != null) {
			this.left.infixOrder();
		}
		System.out.println(this);
		if (this.right != null) {
			this.right.infixOrder();
		}
	}
}

平衡二叉树(AVL)

问题导入

使用数列{1,2,3,4,5,6}创建一棵二叉排序树，将会得到这样一棵树：
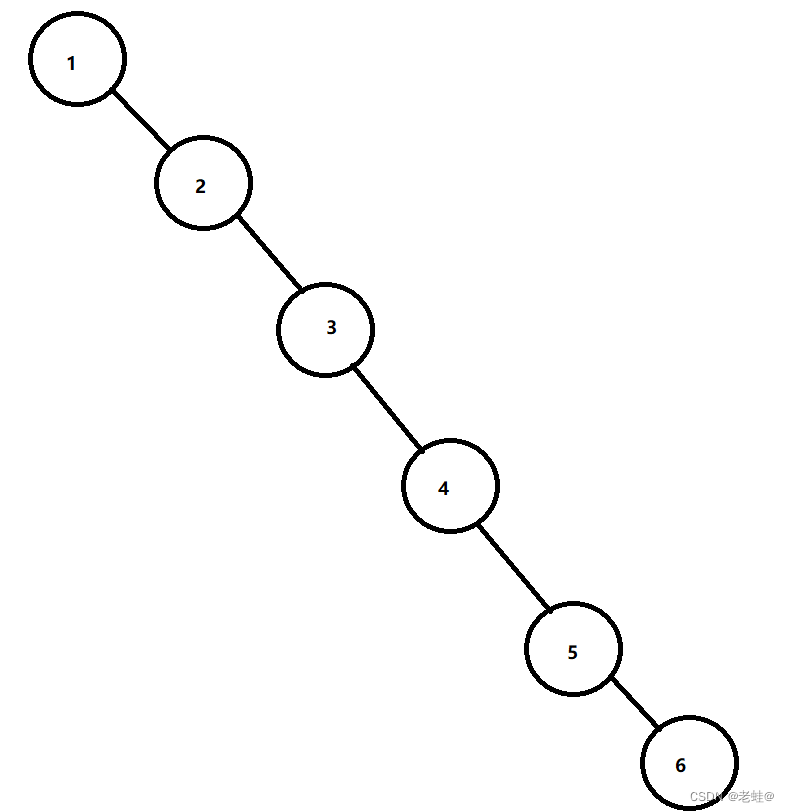
在这里插入图片描述
这棵二叉排序树存在这些问题：

  1. 左子树全部为空，从形式上看，更像一个单链表，失去了树结构的意义
  2. 插入速度没有影响
  3. 查询速度明显降低，不能发挥BST的优势

基本介绍

  1. 平衡二叉树也叫平衡二叉搜索树，又称为AVL树，它可以保证较高的查询效率
  2. 它具有以下特点：它是一颗空树或它的左右两个子树的高度查的绝对值不超过1，并且左右两棵子树都是一颗平衡二叉树，平衡二叉树的常用实现有：红黑树、AVL、替罪羊树、Treap、伸展树等

代码实现

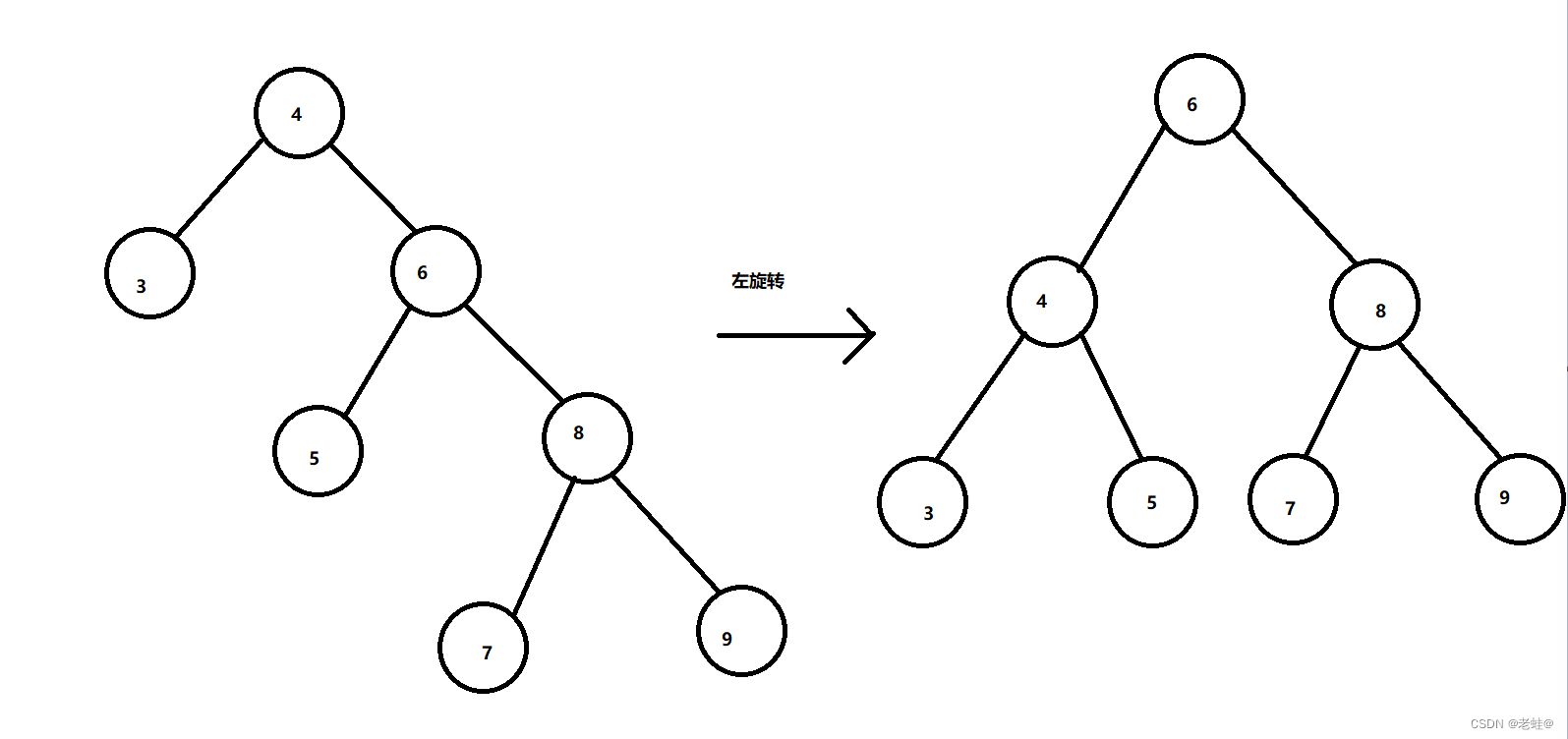
  1. 当右边子树高度高于左边子树高度+1时，进行左旋转
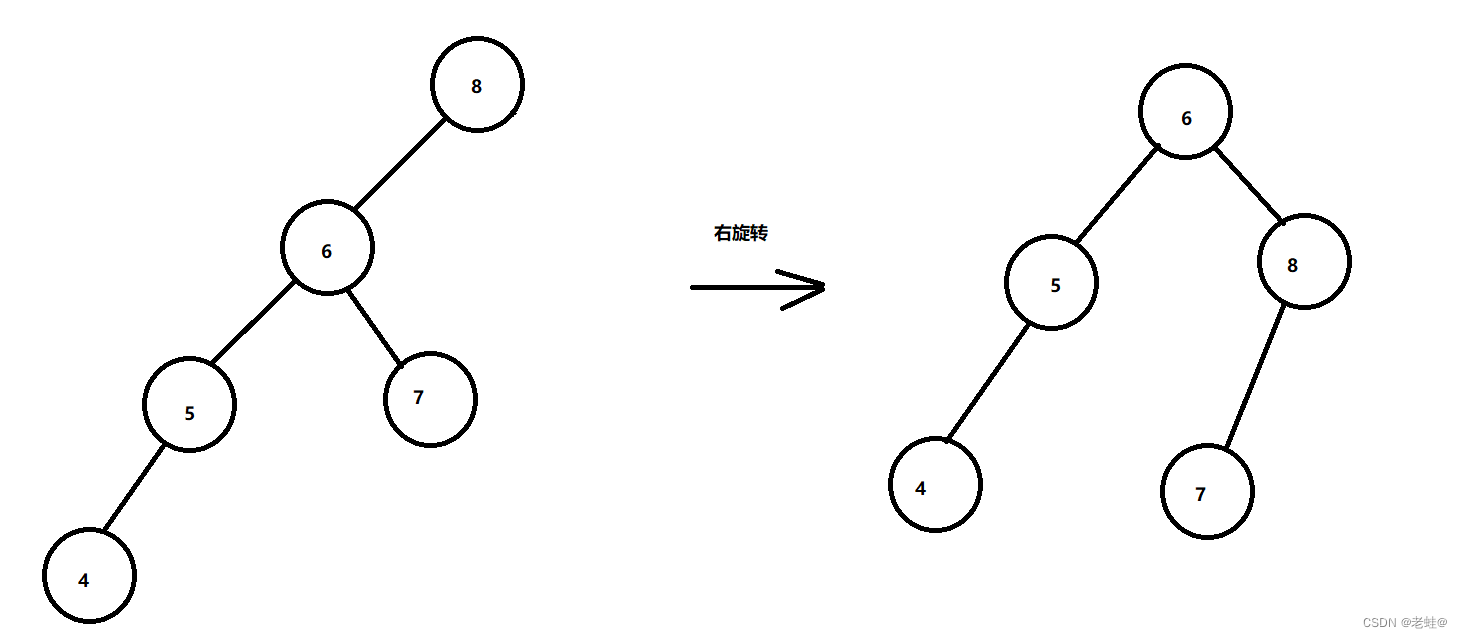
    在这里插入图片描述

  2. 当左边子树高度高于右边子树高度+1时，进行右旋转
    在这里插入图片描述

  3. 当右边子树高度高于左边子树高度+1，并且右子树的左子树高于右边子树+1，左旋转后右子树高的一部分被转到了左子树，这样仍然不平衡，此时需要双旋转，即先将右子节点进行右旋转，让右子树平衡，再让当前结点进行左旋转，对于左子树亦然

/**
 * AVL树
 * 
 * @author laowa
 *
 */
class AvlTree {

	Node root;

	/**
	 * 添加结点
	 * 
	 * @param node
	 */
	public void add(Node node) {
		if (root == null) {
			root = node;
			return;
		}
		root.add(node);
	}

	/**
	 * 获取树的高度
	 * @return 树的高度
	 */
	public int height() {
		return this.root.height();
	}
	
	/**
	 * 删除结点
	 * 
	 * @param no
	 *            需要删除的结点的no
	 */
	public void delete(int no) {
		// 判空
		if (this.root == null) {
			System.out.println("树为空");
			return;
		}
		// 找到目标节点和目标节点的父结点
		Node target = this.search(no);
		// 如果没有找到目标结点直接退出方法
		if (target == null) {
			return;
		}
		Node parent = this.root.searchParent(no);

		// 如果该树只有一颗结点，则直接根结点置空
		if (root.left == null && root.right == null) {
			this.root = null;
			return;
		}

		if (target.left == null && target.right == null) {
			// 如果左右子结点均为空，表示当前结点为叶子结点
			// 找到目标结点在父结点的左边还是右边，然后置空
			if (parent.left == target) {
				parent.left = null;
			} else {
				parent.right = null;
			}
			return;
		}

		// 如果左子结点为空,说明只有一棵右子树
		if (target.left == null) {
			if (parent == null) {
				// 如果父结点为空，即删除的结点是根结点
				this.root = target.right;
			} else {
				// 找到目标结点在父结点的左边还是右边，然后指向目标结点的右边
				if (parent.left == target) {
					parent.left = target.right;
				} else {
					parent.right = target.right;
				}
			}

		}

		// 如果右子结点为空，说明只有一棵左子树
		if (target.right == null) {
			if (parent == null) {
				// 如果父结点为空，即删除的结点是根节点
				this.root = target.left;
			} else {
				// 找到目标结点在父结点的左边还是右边，然后指向目标结点的左边
				if (parent.left == target) {
					parent.left = target.left;
				} else {
					parent.right = target.left;
				}
			}

		}

		if (target.left != null && target.right != null) {
			// 如果目标结点的左右子结点均不为空
			Node temp = target.right;
			// 向左循环查找一直找到最左边的结点，此时temp保存了这个结点
			while (temp.left != null) {
				temp = temp.left;
			}
			// 删除该结点
			delete(temp.no);
			// 将目标结点的左右子结点赋值给该结点
			temp.left = target.left;
			temp.right = target.right;
			// 如果parent为空表示删除的结点是根节点，没有父结点，否则找到目标结点在父结点的左边还是右边，并且设置为temp结点
			if (parent != null) {
				if (parent.left == target) {
					parent.left = temp;
				} else {
					parent.right = temp;
				}
			} else {
				this.root = temp;
			}

		}

	}

	/**
	 * 查找目标结点
	 * 
	 * @param no
	 *            目标结点的编号
	 * @return 结点
	 */
	public Node search(int no) {
		if (this.root == null) {
			return null;
		}
		return this.root.search(no);
	}

	/**
	 * 中序遍历
	 */
	public void infixOrder() {
		if (root == null) {
			System.out.println("树为空");
			return;
		}
		root.infixOrder();
	}
}

/***
 * AVL树结点
 * 
 * @author laowa
 *
 */
class Node {
	int no;
	Node left;
	Node right;

	public Node(int no) {
		this.no = no;
	}

	@Override
	public String toString() {
		return "[Node value=" + no + "]";
	}

	/**
	 * 获取以当前结点为根节点的树的高度
	 * 
	 * @return 一个整数，为以当前结点为根节点的树的高度
	 */
	public int height() {
		// 递归向左右获取高度，去左右高度的最大值，每次获取到会加一，即每一层高度加一
		return Math.max(this.left == null ? 0 : this.left.height(), this.right == null ? 0 : this.right.height()) + 1;
	}

	/**
	 * 获取左子树的高度
	 * 
	 * @return 一个整数，左子树的高度
	 */
	public int leftHeight() {
		return this.left == null ? 0 : this.left.height();
	}

	/**
	 * 获取右子树的高度
	 * 
	 * @return 一个整数，右子树的高度
	 */
	public int rightHeight() {
		return this.right == null ? 0 : this.right.height();
	}
	
	/**
	 * 左旋转
	 */
	private void leftRotate() {
		//以当前结点的值创建一个新的结点，这个新节点后面会被作为左子节点
		Node newNode = new Node(this.no);
		//新结点的左子节点为当前结点的左子节点
		newNode.left = this.left;
		//新节点的右子结点为当前结点的右子节点的左子节点
		newNode.right = this.right.left;
		
		//当前节点的值改为右子节点的值
		this.no = this.right.no;
		//右子节点指向右子结点的右子节点，丢弃右子节点
		this.right = this.right.right;
		//左子节点指向新节点，丢弃左子节点
		this.left  = newNode;
	}
	
	/**
	 * 右旋转
	 */
	private void rightRotate() {
		//以当前结点的值创建一个新的结点，这个结点后面会被作为右子节点
		Node newNode = new Node(this.no);
		//新结点的左子节点指向当前结点的左子结点的右子节点
		newNode.left = this.left.right;
		//新结点的右子节点指向当前结点的右子节点
		newNode.right = this.right;
		
		//将当前节点的值改为左子节点的值，即左子节点上移
		this.no = this.left.no;
		//当前结点左子节点指向左子节点的左子节点，丢弃原来的左子节点
		this.left = this.left.left;
		//当前节点的右子节点指向新节点
		this.right = newNode;
	}

	/**
	 * 查找结点
	 * 
	 * @param no
	 *            结点编号
	 */
	public Node search(int no) {
		if (this.no == no) {
			// 如果当前结点为需要查找的结点，返回
			return this;
		}
		if (this.no > no) {
			// 如果目标编号小于当前结点，表示目标结点在左边
			if (this.left != null) {
				return this.left.search(no);
			}
			// 没找到
			return null;
		}
		// 如果目标编号大于当前结点，表示目标结点在右边
		if (this.right != null) {
			return this.right.search(no);
		}
		// 没找到
		return null;
	}

	/**
	 * 查找结点的父结点
	 * 
	 * @param no
	 * @return
	 */
	public Node searchParent(int no) {
		// 如果作右子结点中存在目标结点，则放回当前结点
		if ((this.left != null && this.left.no == no) || (this.right != null && this.right.no == no)) {
			return this;
		}
		// 如果当前结点大于目标结点，向左递归查找
		if (this.no > no && this.left != null) {
			return this.left.searchParent(no);
		}
		// 如果当前结点小于目标结点，向右递归查找
		if (this.no < no && this.right != null) {
			return this.right.searchParent(no);
		}
		// 没找到返回null
		return null;
	}

	/**
	 * 添加结点
	 * 
	 * @param node
	 *            待添加的结点
	 */
	public void add(Node node) {
		// 判空，添加的结点为空则不添加
		if (node == null) {
			return;
		}
		if (node.no < this.no) {
			// 如果待添加的结点小于当前节点，想左子树添加
			if (this.left == null) {
				// 如果左子节点为空则直接加载左边
				this.left = node;
			} else {
				// 否则向左子结点递归添加
				this.left.add(node);
			}
		} else {
			// 如果待添加的结点大于或等于当前结点，向右子树添加
			if (this.right == null) {
				// 如果右子节点为空则直接加在右边
				this.right = node;
			} else {
				// 否则向右子结点递归添加
				this.right.add(node);
			}
		}
		
		//当右子树的高度-左子树的高度之后大于1，进行左旋转
		if(this.rightHeight()>this.leftHeight()) {
			//如果右子节点的左子树高度-右节点的右子树高度>1，先让右子树平衡
			if(this.right!=null&&this.right.leftHeight()>this.right.rightHeight()) {
				this.right.rightRotate();
			}
			this.leftRotate();
			//当左子树的高度-右子树的高度之后大于1，进行右旋转
		}else if(this.leftHeight()>this.rightHeight()) {
			//如果左子节点的右子树高度-左节点的左子树高度>1，先让左子树平衡
			if(this.left!=null&&this.left.rightHeight()>this.left.leftHeight()) {
				this.left.leftRotate();
			}
			this.rightRotate();
		}
	}

	/**
	 * 中序遍历
	 */
	public void infixOrder() {
		if (this.left != null) {
			this.left.infixOrder();
		}
		System.out.println(this);
		if (this.right != null) {
			this.right.infixOrder();
		}
	}
}

多叉树

二叉树的问题分析

二叉树需要加载到内存，如果二叉树的结点少，没有什么问题，但如果二叉树的结点非常多(比如上亿)，就存在如下问题：

  1. 再构建二叉树时，需要进行多次操作(海量数据存在数据库或者文件中)，结点海量，构建二叉树时的速度就慢
  2. 结点海量也会操作二叉树的高度很大，降低其他的操作速度

多叉树

  1. 在二叉树中每个结点有数据项，最多两个子结点，如果允许每个结点可以有更多的数据项和更多的子结点，就是多叉树
  2. 如2-3树，2-3-4树就是多叉树，多叉树通过重新组织结点，降低树的高度，提高树的操作速度

2-3树

  1. 2-3树的所有结点都在同一层(只要是B树都满足这个条件)
  2. 有两个子结点的结点，叫做二节点，二节点要么没有子结点要么有两个子结点
  3. 有三个子结点的结点叫做三节点，三节点要么没有子节点要么有三个子结点
  4. 2-3树就是有二节点和三节点构成的树
    在这里插入图片描述

B树、B+树、B*树

B树

B-tree即B树而不是B-树，B即Balance；如2-3树和2-3-4树都是B树

  1. B树的阶：结点的最多子结点个数，比如2-3树的阶是3，2-3-4树的阶是4
  2. B树的搜索，是从根节点开始，对结点内的关键子序列进行二分查找，如果命中则结束，否则进入查询关键字范围的子结点，重复找直到找到对应的子结点为空或已经是叶子结点
  3. 关键字集合分布在整棵树中，即叶子节点和非叶子节点都存放数据
  4. 其搜索性能等价于在关键字全集内进行一次二分查找

B+树

B+树是B树的变体，也是一种多路搜索树

  1. B+树的搜索与B树也基本相同，区别在于B+树只有达到叶子结点才会命中，即真实数据只存在于叶子结点，其性能也相当于关键字全集内进行一次二分查找
  2. 所有关键子都出现在叶子结点的链表中，(即数据值能在叶子结点[也叫稠密索引])，且链表中的关键字恰好是有序的
  3. 非叶子结点相当于是叶子节点的索引(稀疏索引)，叶子结点相当于存储数据的数据层
  4. B+树更适合文件索引系统
  5. B树和B+树各有各自的适合的场景，不能说那一个完全更好

B*树

B*树是B+树的变体，也是一种多路搜索树

  1. B树定义了非叶子结点关键字个数至少为2/3M，即块的最低使用率为2/3，而B+树块的利用率为1/2
  2. B*树分配新结点的概率比B+树要低，空间使用率更高
老蛙@
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
二叉排序树与平衡二叉树的实现
04-08
题　目 二叉排序树与平衡二叉树的实现 1、课程设计的目的 使学生进一步理解和掌握课堂上所学各种基本抽象数据类型的逻辑结构、存储结构和操作实现算法，以及它们在程序中的使用方法。 使学生掌握软件设计的基本内容...
数据结构与算法设计课程设计二叉排序树与平衡二叉树.doc
07-06
数据结构与算法设计是计算机科学中的核心课程，其在本次课程设计中主要关注的是二叉排序树和平衡二叉树。二叉排序树是一种特殊的二叉树，它满足以下特性：每个节点的左子树只包含小于当前节点值的节点，而右子树则...
C语言-实现顺序二叉树和平衡二叉树AVL
mike_jun的博客
04-10 1069
在实现二叉树之前先看下结构体的一些使用方法数组是保存一系列相同的数据。在实际问题中，一组数据往往有很多种不同的数据类型。例如，登记学生的信息，可能需要用到 char型的姓名，int型或 char型的学号，int型的年龄访问其中的各个元素，用结构成员运算符点（.）。即访问成员的一般形式是：结构变量名 . 成员名如 a.name 表示学生 a 的姓名。1）结构体的成员逐个赋值2）整体赋值也可以在初始化的时候赋值3）整体拷贝如上每次使用结构体均需要写struct，可以使用typedef 简化书写。
数据结构之二叉排序树
qq_47897078的博客
05-27 1808
数据结构之二叉排序树 1、二叉排序树定义 二叉排序树也叫二叉搜索树、二叉查找树。二叉排序树树是一颗它的左子树上的节点都小于根节点，右子树上的节点都大于根节点的二叉树，且其左右子树也是二叉排序树。 实例 二叉树实例 2、二叉排序树的创建 当要向二叉排序树中插入元素的时候，从根节点开始查找，先将根节点作为当前节点，如果要插入的值比当前节点的值小，则判断当前节点的左孩子是不是空，如果是空则将要插入的值作为当前节点的左孩子，不是空则将当前节点的左孩子作为当前节点继续查找；当要插入的值比当前节点的值大时，判断当前节
平衡二叉排序树
Snowball
08-23 1721
AVL树介绍 BST是一种查找效率比较高的组织形式，但其平均查找长度受树的形态影响较大，形态比较均匀时查找效率很好，形态明显偏向某一方向时其效率就大大降低。因此，希望有更好的二叉排序树，其形态总是均衡的，查找时能得到最好的效率，这就是平衡二叉排序树。     平衡二叉排序树(Balanced Binary Tree或Height-Balanced Tree)是在1962年由Adelson-Ve
二叉树、自平衡二叉树和多叉树详解
快乐的小三菊的博客
10-21 1762
二叉树、自平衡二叉树和多叉树简单介绍，以及排序方式
二叉树与多叉树
wangzilong_2019的博客
05-10 1298
序言 多叉树 2-3树 B树 B+树 B*树 序言 二叉树的缺点 二叉树需要加载到内存中，如果节点少，没什么问题，若是节点非常多，就会带来问题 当构建二叉树时，需要进行多次I/O操作，构造速度会有影响 节点海量，会造成二叉树的高度非常大降低操作速度 多叉树 每个节点可以右多个子节点 B树 节点的度：此节点拥有子节点的个数称为节点的度 数的度：数中所有节点的度的最大值 B树通过重新组织节点，降低了数的高度 文件系统或是数据库系统利用了磁盘预先读取原理，将一个节点的大小设置为一个页（一个页的大小为4
实现二叉排序树的各种算法
07-25
二叉排序树（Binary Sort Tree，BST），也称为二叉查找树或二叉搜索树，是一种自平衡的二叉树数据结构，它在处理搜索、插入和删除操作时具有较高的效率。二叉排序树的主要特性是：对于任意节点，其左子树中的所有...
二叉树的应用：二叉排序树BST和平衡二叉树AVL的构造 课设作业 完整代码
02-10
其定义为：二叉排序树或者是空树，或者是满足如下性质的二叉树：1.若它的左子树非空，则左子树上所有结点的值均小于根结点的值；2.若它的右子树非空，则右子树上所有结点的值均大于根结点的值；3.左、右子树本身又各...
数据结构实验：判断一棵二叉树是否是二叉排序树
最新发布
10-17
一棵空树，或者是具有下列性质的二叉树： （1）若左子树不空，则左...（3）左、右子树也分别为二叉排序树； 思路： 1.首先构建一棵二叉树 2.根据二叉排序树的性质写一个判断函数 3.通过函数判断是否为一颗二叉排序树
多叉树的实现
05-22
多叉树的实现，本算法采用5比较合适，纵向遍历靠递归调用
二叉树和多路查找树
qq_43761048的博客
02-29 286
二叉树 二叉树效率较高，但是也存在很多问题，二叉树需要加载到内存中，如果二叉树结点少，则问题不大，如果结点较多（比如按亿为单位） （1）在构建二叉树时，要进行多次I/O操作，构建二叉树的速度会有影响。 （2）结点海量会造成二叉树的高度很大，从而引起操作较慢的后果。 多叉树 二叉树中每个结点有数据项，最多有两个子节点，如果允许每个节点允许有更多数据项和更多个子节点，则是多叉树。 （1）B树通过重新组...
二叉排序树的基本操作
m0_61886762的博客
05-26 1399
二叉排序树（Binary Sort Tree），又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树。 （1）若它的左子树不空，则左子树上的所有结点的值均小于它的根结点的值。 （2）若它的右子树不空，则右子树上的所有结点的值均大于它的根结点的值。 （3） 它的左、右子树也分别为二叉排序树。 1.1 二叉排序树的查找操作 首先二叉树的结构为： typedef struct BitNode { int data; struct B...
二叉排序树的构造与插入(初版)
theonepiece的博客
08-25 1799
定义: 一棵空树，或者是具有下列性质的二叉树： 若左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若右子树不空，则右子树上所有结点的值均大于它的根结点的值； 左、右子树也分别为二叉排序树； 没有键值相等的结点。 结构体定义: typedef struct BTNode { int key; struct BTNode* lchild; struct BTNode* rchild; }BTNode; 二叉排序树的插入算法： int BSTInsert(BTNode *&bt,
用二叉树的方式表示多叉树
矢月的博客
03-14 1150
以下内容分为三部分： 1.链表结构 2.多叉树到二叉链表的表示 3.二叉链表表示法的遍历 1.链表结构： 二叉链表表示法又被叫做左儿子右兄弟表示法（在第二部分会加以解释） struct TNode{ int data; TNode *parent;//上层节点 TNode *firstchild;//第一个子节点 TNode *nextsibling;//同一层次的相邻...
二叉树和N叉树的前序遍历
qq1344574215的博客
09-09 124
二叉树： class Solution: def preorderTraversal(self, root: TreeNode) -> List[int]: if not(root): return [] stack = [root] res = [] while(stack): cur_node = stack.pop() res.append(cur_
树的遍历（二叉树、N叉树）
weixin_42638946的博客
02-28 324
树的遍历 一. 二叉树的遍历 二叉树的定义 C++ struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; Java public class TreeNode { int val; TreeNode left; TreeNode right; TreeN

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值