CSU_科学计算与数学建模_学习笔记（5）

科学计算与数学建模，郑洲顺老师
平台——学堂在线 https://www.xuetangx.com/course/CSU07011000630/5882763?channel=learn_title

湘江水流量估计的实际意义

利用牛顿 - 莱布尼茨公式算出定积分—— 得到河流横截面的面积，流速得到流量
我们希望原函数在F(a), F(b)上容易计算

但是，在工程技术和科学研究中，常常遇到如下情况：
（1）f(x)被积函数本身复杂，求原函数困难
（2）f(x)原函数不能用初等函数表f示
（3）f(x)的精确表达式未知，只有一张实验数据表

+问题，什么是更方便得到数值积分近似值的方法？

• ——需要被积函数在给定区间上足够多个点的信息，用**近似函数φ(x)**的定积分，作未知函数f(x)定积分的近似值
• 理想情况下 |φ(x)- f(x)| << 1， 并且定积分误差也足够小

+问题，函数误差足够小，导数误差不一定足够小——>数值微分处理中，不能直接用近似函数的微分作未知函数的微分近似值
+那么积分处理下，成立还是不成立呢？

• 因为定积分具有可比性，又由于|φ(x) - f(x)|<<η，那么|φ(x) - f(x)|的积分一定小于η在同样区间上的积分，因此，只要η足够小，误差是在可控范围内的

构造数值求积公式的基本方法

利用拉格朗日插值多项式构造——> 算多项式的积分 = 相应节点处函数值和相应节点处拉格朗日插值基函数在整个区间定积分的乘积再累加——> 定积分得到的数值记作Ak
几何上，相当于将曲边梯形分成n+1个矩形高度的和
因此，取适当宽的Aηk，就可以近似计算原函数定积分，称为机械求积公式
+问题，什么是适当的宽度？
Ak用对应的拉格朗日插值函数来算，插值型求积公式
+pad笔记，拉格朗日基函数的表示：

积分的真值与某求积公式给出的近似值之差，称为该求积公式的余项，记作R[f]

插值型求积公式的余项

求积公式的代数精度
+问题，哪种数值求积公式更好？什么标准？
——代数精度足够的高

+pad笔记，几何含义：n+1个节点的插值多项式围成的面积 = n+1个矩形围成的面积的和

• 找到一个同样的标准，代入特殊值f(x) = 1, x, x^2,…, x^m
• 用m，定积分公式成立的最高次幂，来表征求积公式的代数精度

定理
含有n+1个节点xk的插值型求积公式，代数精度至少为n

+问题，对于给定的n+1个求积节点，有无数多个近似定积分公式，那么其中是否存在最好的机械积分公式？

Newton-Cotes积分法

机械积分：相应点处的函数值和任意一组适当的常数相乘相加
用插值多项式代替被积函数，是其中最好的方法

求积节点互异—— 方程组系数矩阵所构成的行列式就是范德蒙行列式—— 只要节点互异，方程组存在唯一解
（1）用拉格朗日基函数求出最好
（2）用解方程组的方式求出最好
—— 机械积分公式中最好的求积公式唯一，且就是插值型的公式，用方法（2）难解，用方法（1），把拉格朗日基函数求出——>得到定积分的近似函数
牛顿柯特斯公式的定义，区间等分，插值型定积分

+pad笔记，换元积分

把(b-a)留下，剩下部分记作C(n)k, Ak=(b-a)C(n)k
将定积分的近似计算，转换成牛顿柯特斯公式
可以计算出一张Cotes表：

一等分、二等分、四等分的展开公式
（即梯形公式、辛普森公式、牛顿柯特斯公式）
特别的，在五点公式（即四等分公式）为牛顿柯特斯公式
而插值多项式近似函数，不是次数越多越好在实际应用中，常见的最高等分数为六等分

+认知
Cotes系数作被积近似函数系数的优势：只要给出积分区间的等分数、区间的跨度，就可以直接计算出Cotes系数——>进而得到定积分近似值（而不需要知道具体节点的位置）

复合积分公式

问题背景：由于柯特斯公式为 (b-a)Cn_k = Ak，该近似值和真实值之间的余项大小与（b-a）跨度的高次幂有关，而等距时情况下，等分点n会很多，区间（a-b）跨度大，含(b-a)高次幂的余项数值大，误差增加
+问题，不是n越大越好，如何改进？

复合Newton-Cotes公式

+课堂截图，复合梯形公式
分成小区间，在每个小区间上应用相应公式，再相加
得到复合梯形公式，或复合Simpson公式，或复合Cotes公式（根据每个小区间应用的公式不同）

定义收敛阶

+pad笔记

用复合积分公式的误差和步长h的同阶无穷小的阶数——>定义收敛阶
复合求积公式Tn, Sn, Cn收敛阶分别为二阶、四阶和六阶

总结牛顿柯特斯的等分插值算法：

• 算一个曲边梯形面积的方法，先n等分，再逐次地等分下去，尽快达到精度的要求

+问题，基于已有的结果，如何更快构造精度更高的数值积分？

Romberg算法

利用上述图片中的复合梯形公式的 T2n与Tn的递推公式，
可以简单方便产生梯形序列{T2^k}，但是收敛速度非常慢
比如，已知派的积分公式，为函数（4/(1+x^{2)）在区间[0,1]的积分数值，如果采用复合梯形公式递推的办法，要算到T的512项，才能达到10}-6精度

+思考，提高收敛速度，节约计算工作量
在{Tn^k}序列基础上，作线性组合，就可产生收敛速度更快的Simpson序列，
在{Sn^k}序列基础上，作线性组合，就可产生收敛速度更快的Cotes序列，
…> Romberg序列
+ipad笔记，Romberg算法思想

+课堂笔记，Tn_k记号

• 定义：一种对复合梯形产生的近似值进行加权平均，以获得逐步提高精度的算法

• 优点：公式简练、使用方便、结果可靠

+问题，现在能做的都只是在给定求积节点下算出积分近似值
当等距时，牛顿柯特斯+荣贝格算法
在现实中，如果这些节点不给定，能否通过节点的选择来提高精度？

Guass积分方法

如何测量，足够少的点，达到精度要求？
+ipad笔记

+课堂截图，精度达到3，需要两个求积节点和两个求积系数确定（2n+2）个常数，即要找到求积节点和对应的求积系数，使积分公式精度达到2n+1—— Guass型求积公式

• 第1步，用区间[a,b]上的n+1次正交多项式确定Guass点，Xk
• 第2步，利用这些Guass点确定求积系数，Ak

常用高斯节点

+课堂截图，常用高斯公式节点和系数

用数学结论解决实际问题
+ipad笔记，n=3查表得到三点的高斯型求积公式

+思路，如果要进一步提高进度，不需要增加节点数（未必误差会缩小），而可以采用用低次插值的思想，分段插值的思想
首先，分成m个小区间
再用复合积分方法做，每个小区间同样用高斯区间做（即2，3，4，5个点已经足够使用）
+pad笔记，实例，利用四点高斯型求积公式计算派的近似值

复合高斯公式的迭代过程

• 将积分区间[a,b]分成m个等长的小区间[x_(i-1),x_(i)]

• 在每个小区间上使用低阶的Guass型求积公式

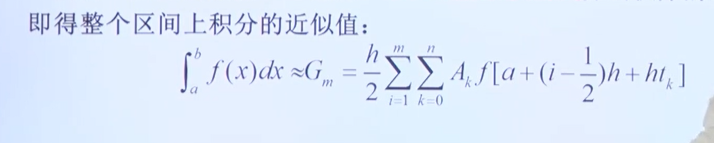
• n个点的高斯积分公式，m个小区间上的积分公式

• 并不断增大m，当Δ在给定误差内，就停止计算

<——数值积分的基本方法，到此结束