统计检验问题:Friedman Test,Nemenyi test检验和Bonferroni-Dunn test检验

白小沫

已于 2023-03-09 10:47:03 修改

阅读量9.3k

点赞数 21

分类专栏：笔记文章标签：经验分享

于 2023-02-19 14:23:42 首次发布

本文链接：https://blog.csdn.net/m0_49354332/article/details/129110091

版权

笔记专栏收录该内容

17 篇文章

订阅专栏

当我们提出一个算法后，我们需要将它与其他的算法进行对比，表现出它们的性能差异。因此，在做算法对比时，往往需要对实验结果进行统计检验。一般会先利用弗里德曼检验判断提出算法是否与其他算法有明显的差异，如果有的话还需要继续进行后续的统计检验，比如用Nemenyi test检验和Bonferroni-Dunn test检验。

Friedman test是一种常用的检验，用来比较k个算法在N个数据集上的整体表现性能。但Friedman test只能给出k个算法的性能之间是否存在差异的结论，如果存在差异，还需要进行“后续检验”(post-hoc test)，以得出哪些算法的性能之间存在统计上的差异，常用的后续检验方法包括Nemenyi test和Bonferroni-Dunn test。

Nemenyi test适用于对比k个算法相互之间的性能(when all classifiers are compared to each other)，【这个方法提出了 Critical Difference 的概念，并且可以通过作图来呈现结果。CD具体的计算在 06 JMLR那篇有详细介绍。】
链接：https://www.jmlr.org/papers/volume7/demsar06a/demsar06a.pdf

CD的计算公式如下：
在这里插入图片描述

域值（critical difference, CD)CD图：用来表示不同算法之间的性能差异，图形如下：
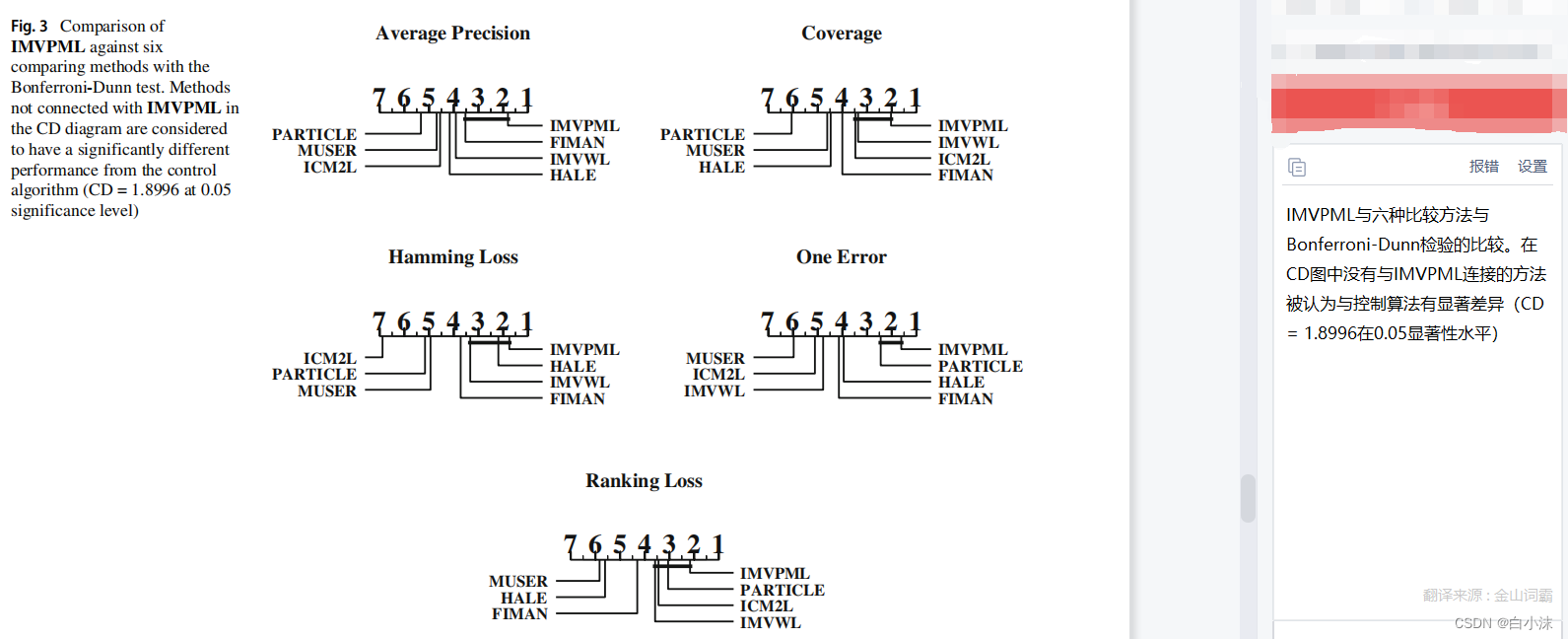
在这里插入图片描述

周志华书本上对两种检验的描述如下：
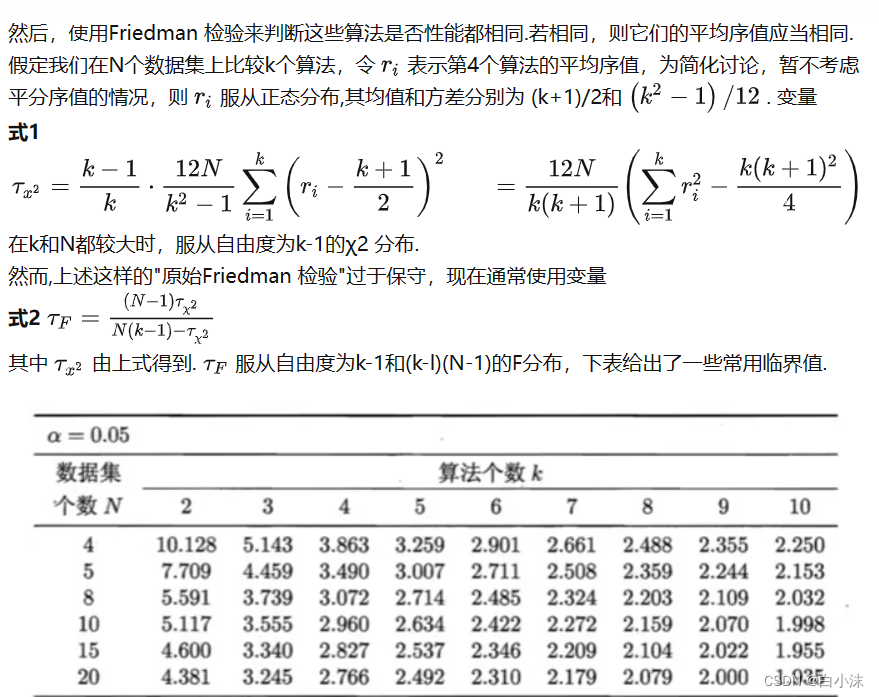
在这里插入图片描述

如果算法之间有横线相连说明提出的算法性能不显著；如果没有横线相连，说明所提出的算法性能显著。

而Bonferroni-Dunn test适用于将某个算法与其余k-1个算法对比(when all classifiers are compared with a control classifier)，二者都是将各个算法平均排名之差与某域值（critical difference, CD)对比，若大于该域值则说明平均排名高的算法统计上优于平均排名低的算法，反之则二者统计上没有差异。

实例：
在这里插入图片描述
这里的F0.05和F0.1可以根据给定的算法个数和数据集个数，根据对应的F表格查值，如果无法查到的话，只能借助软件R语言，python或者matlab进行计算，然后再进行比较

实践部分：因为一直想复现出论文中关于Friedman检验图时如何画出来的，所以参考了CSDN中很多优秀博主的帖子，经过自己的实践后，发现比较有效的方法是以下两种方法：
Matlab中实现Friedman检验：
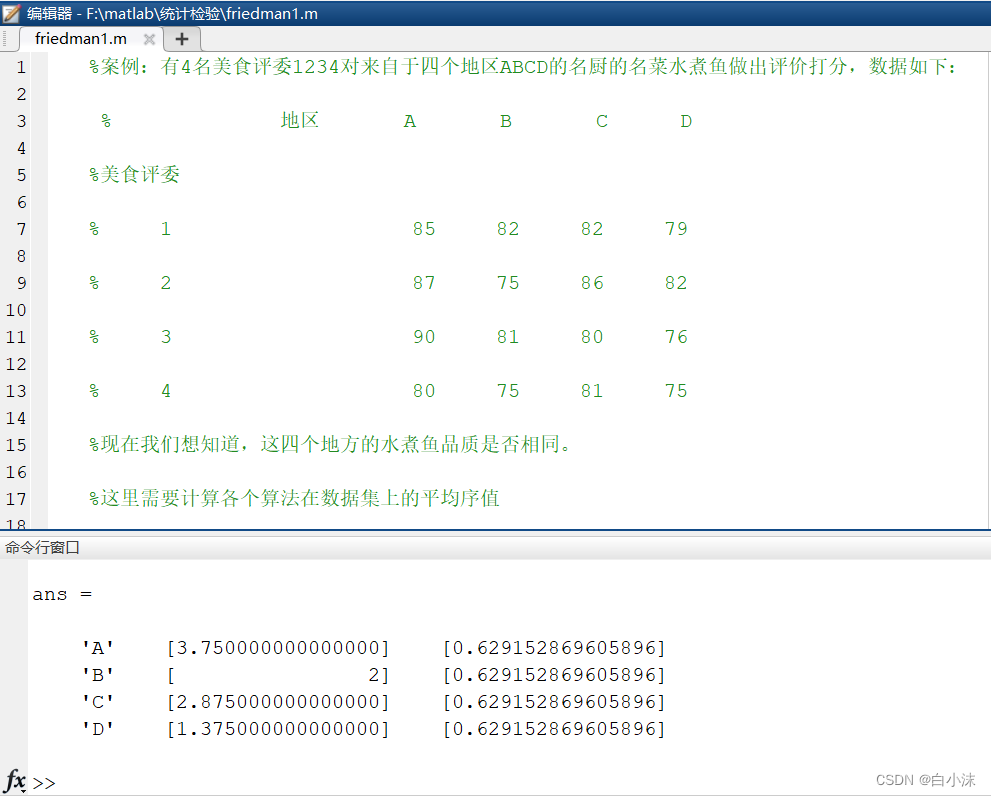
在这里插入图片描述

Python中实现Friedman检验：

在这里插入图片描述
请添加图片描述
3.利用python中的Orange模块来进行绘图，但是这个容易出现以下的错误，比如会出现导Orange包无法导入，即Orange包一直无法安装等问题，这时可以试试离线下载。不过下载完成后，在进行Friedman检验时，可能会报错，结果报错显示AttributeError: module ‘Orange.evaluation’ has no attribute ‘compute_CD’，这个错误截至现在发文，我还没有找到好的解决方法。
4.手算出各个算法在各个数据集上的平均序值，通过公式计算得到CD值，然后利用PPT或者Word手绘出检验图
5.平均序值的计算，实例部分：
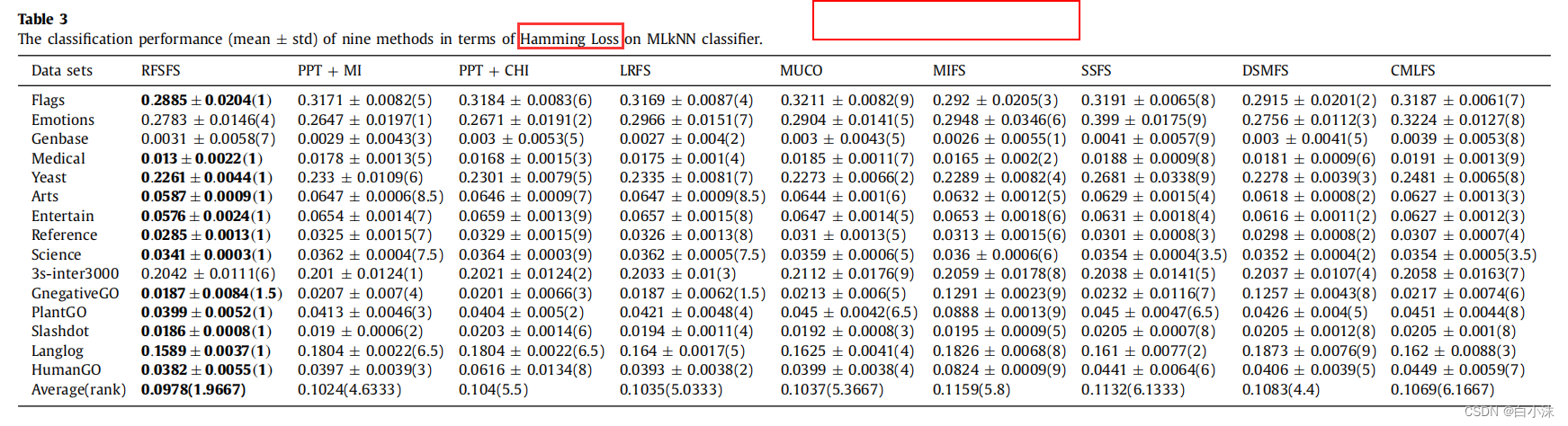
在这里插入图片描述

参考文章：
1.统计检验–多个算法在多个数据集上的结果比较及R语言实现 - 知乎 (zhihu.com)
2.https://blog.csdn.net/jbb0523/article/details/109990924
3.https://blog.csdn.net/QKK612501/article/details/123903124?4.spm=1001.2101.3001.6650.7&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-7-123903124-blog-129110091.pc_relevant_multi_platform_whitelistv3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-7-123903124-blog-129110091.pc_relevant_multi_platform_whitelistv3&utm_relevant_index=8
5.https://zhuanlan.zhihu.com/p/266217635
6.https://zhuanlan.zhihu.com/p/145831286