目录
前言
五一假期过了,后续还有毕设答辩一堆事情。现在能复习多少是多少吧。
今天复习树的存储结构、森林以及哈夫曼树。
一、树的存储结构
1 双亲表示法(顺序存储)
基本思路:每一个结点中存储一个指向双亲的指针。

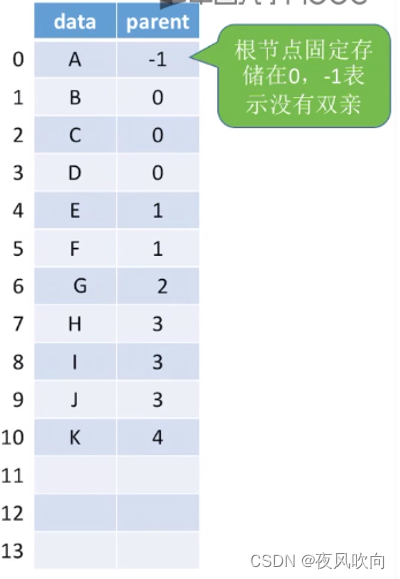
基本操作中,增改查与顺序存储的方式并无区别,只需要在修改数据data的同时注意指针parent即可。但是删除操作有两种方案:1、由于仅有根结点位于0号位且其指针parent的值为-1,所以删除一个结点后,可以将其指针parent置为-1表示该结点已被删除;2、用另一个结点的数据将被删除结点覆盖。
使用顺序存储的优点:方便寻找任意结点的双亲结点。
缺点:1、查找指定结点只能从头遍历;2、删除操作若采用方案一,则当“空数据”增加时,会导致遍历时间增加(可以使用方案二解决)
#define MaxSize 20 //设置树中最大结点数
typedef struct { //定义结点
ElemType data; //数据
int parent; //父结点指针
} TreeNode;
typedef struct { //定义树
TreeNode nodes[MaxSize]; //结点集
int n; //树当前结点总数
} Tree;2 孩子表示法(顺序+链式)
基本思路:顺序表中存储一个指向第一个孩子结点的指针*firstChild,同时每一个孩子结点都用指针指向它的下一个兄弟结点。最后记录根结点所在位序。


基本操作:
1、增:若父结点无孩子结点,则将父结点的*firstChild指针指向新增结点;若有兄弟结点,则将最后一个兄弟结点的指针指向新增结点。同时将新增结点记录到表格中,并将其*firstChild指针指向NULL。
2、改、查:从头遍历。
3、删:从头遍历找到要删除结点的父结点、兄弟结点,然后注意删除后其子结点的归属。需要用到单链表删除以及顺序存储的删除思想。
#define MaxSize 20 //设置树中最大结点数
typedef struct LinkNode { //定义孩子链表
int child; //孩子结点所在位置
struct LinkNode* next; //下一个孩子结点指针
} ChildNode;
typedef struct { //定义顺序表的结点
ElemType data; //数据元素
struct LinkNode* firstChild; //指向第一个孩子结点的指针
} ParentNode;
typedef struct { //定义树
SqNode nodes[MaxSize]; //结点集
int n, r; //树当前结点总数与根结点所在位置
} CPTree;3 孩子兄弟表示法(链式存储)
基本思路:左指针视为孩子指针,右指针视为兄弟指针。将第一个孩子结点用孩子指针连起来;当前结点的下一个兄弟结点用兄弟指针连起来。
这样就可以将树转化为二叉树。

二、森林
森林就是 m(m≥0) 棵互不相交的树的集合
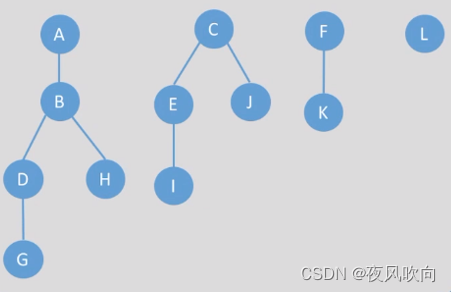
如图所示,这四棵树组成了一个森林。
森林的存储方式与上文提到的孩子兄弟表示法类似。也是孩子指针指向第一个孩子结点;兄弟指针指向下一个兄弟结点。
三、树与森林的遍历
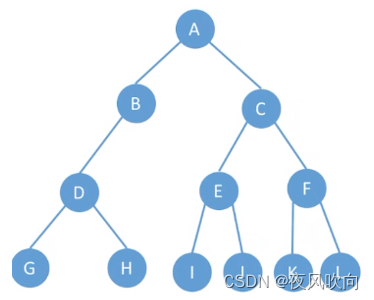
1 树的先根遍历(深度优先)

若根结点不为空,则访问该结点;随后对根结点的子树依次进行先根遍历。
以此树为例,先根遍历得到的结果是:A B E K F C G D H I J
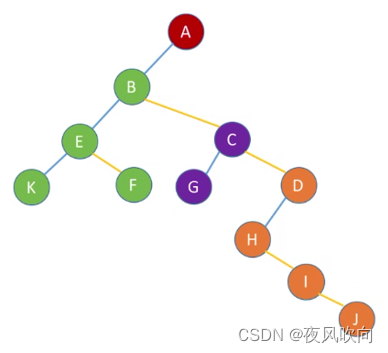
将该树化为二叉树形式,会发现树的先根遍历得到的结果与该树所对应二叉树的先序遍历结果一致。
2 树的后根遍历(深度优先)
与先根遍历相对应,若存在子树,则优先依次对子树进行后根遍历,最后再访问当前结点。
以上图为例,后根遍历结果为:K E F B G C H I J D A
所化二叉树的中序遍历结果一致。
3 树的层次遍历(广度优先)
与二叉树的层次遍历一致,都需要构造一个辅助队列。
1、将根结点入队
2、若队列不空,队头结点出队,访问该结点,并将其子结点依次入队
3、重复步骤2,直至队空
4 森林的先序遍历
由于森林就是多棵树的集合,因此有两种方案进行选择:
1、对每棵树依次进行先根遍历
2、对森林转化为的二叉树进行先序遍历
5 森林的中序遍历
一样有两种方案:
1、对每棵树依次进行后根遍历
2、对森林转化为的二叉树进行中序遍历
6 小结
由于树的遍历没有中根遍历,且无法与二叉树中的后序遍历相对应。因此除去层次遍历,树与森林的遍历方式目前来看只有两种。
四、哈夫曼树
1 基本概念与术语
1、结点的权:有某种现实含义的数值(如:表示结点的重要性等)
2、结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点权值的乘积
3、树的带权路径长度:树中所有叶节点的带权路径长度之和 (Weighted Path Length, WPL)
4、哈夫曼树定义:在含有 n 个带权叶节点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称为最优二叉树
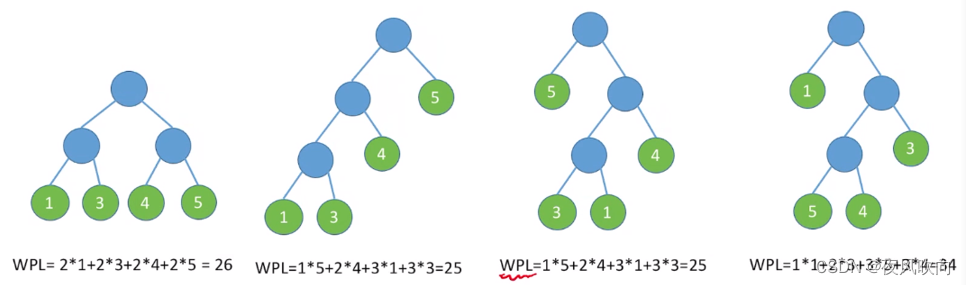
如图所示,树2、3是哈夫曼树,树1、4不是。
2 哈夫曼树的构造
思路:
1、将 n 个结点视为 n 棵仅有一个结点的二叉树,它们组成了一个森林
2、选取根结点权值最小的两棵树,将其作为新结点的左右子树,新结点的权值为两棵子树根结点权值之和
3、从森林中删去选取的两棵树,并将新生成的树加入森林
4、重复步骤2、3,直至仅剩一棵树
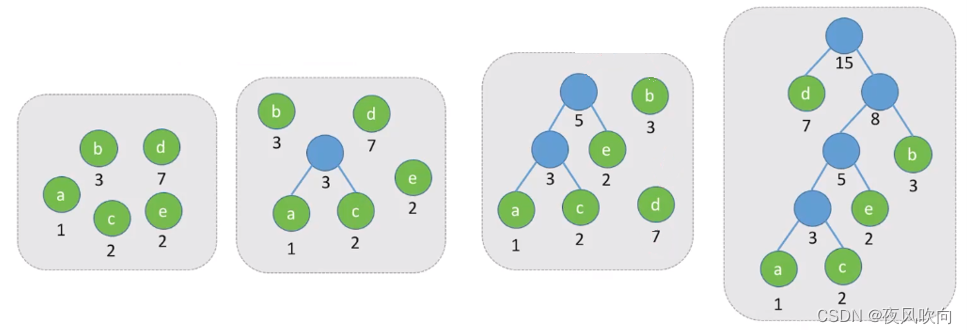
如图,此时WPL为1*4 + 2*4 + 2*3 + 3*2 + 7*1 = 31
3 哈夫曼树的特点
1、每个初始节点最终都成为叶节点,且权值越小的结点到根结点的路径长度越大
2、哈夫曼树的结点总数为 2n - 1
3、哈夫曼树中不存在度为 1 的结点
4、哈夫曼树并不唯一,但 WPL 必然相同且为最优
4 哈夫曼编码
1 哈夫曼编码的定义
字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,以此来进行哈夫曼树的构建,最后得到结果就是哈夫曼编码的结果。
2 补充
1、固定长度编码:每个字符用相等长度的二进制位表示

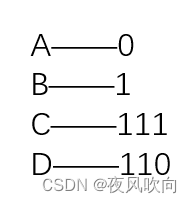
如图,ABCD都用长度为2的二进制位表示,这就是固定长度编码
2、不定长度编码:允许对不同字符用不等长的二进制位表示
3、若不定长度编码中,没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码,例如哈夫曼编码。前缀编码不会出现歧义。
4、若存在一个编码是另一个编码的前缀,则称这样的编码为非前缀编码。非前缀编码可能会出现歧义。
如图,若传输信号为ABBBD,那么接收端可能会将信号理解成ACD,这就是非前缀编码会产生的歧义现象。
五、并查集
从我的角度理解,并查集的“集”就是树的集合(森林),可以对树进行“并”与“查”的操作
查——找到当前结点属于哪一个集合(找到所在树的根结点)
并——将两个集合并为一个集合(两棵树变成一棵树)
1 存储结构——双亲表示法(顺序存储)
见树的存储结构,双亲表示法
双亲表示法就是在结点中添加一个int类型的变量parent,用于存储其父结点所在位置的下标(或者使用一个对应大小的数组来记录)。与树的双亲表示不同的是,并查集中每棵子树的根结点的parent记为-1,且没有删除与修改的功能。
其初始化的形式如下图所示
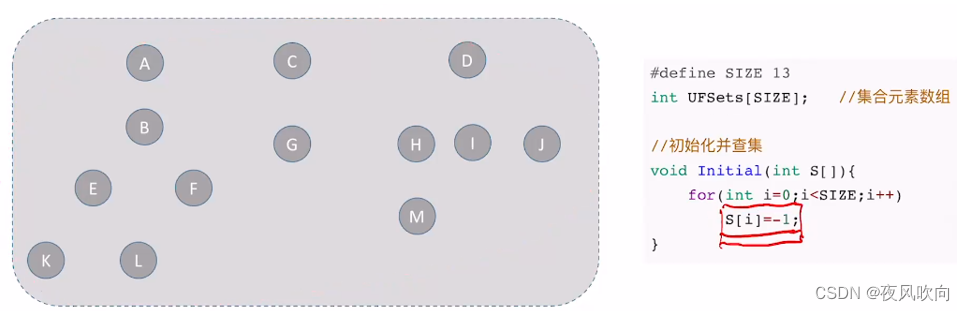
如图,初始化时,是使用数组来表示集合,其中 S[i] 便是森林中下标为 i 的结点的父结点的下标(即parent),初始全都置为-1。需要通过并操作使其连接起来。
2 并查操作
//查操作
TreeNode Find(TreeNode node, Forest trees) {
while(node.parent != -1) {
node = trees.nodes[node.parent];
}
return node;
}
//并操作
void Unit(Forest trees, TreeNode root1, TreeNode root2){
//若两棵树一样,
if(root1下标 == root2下标) return;
root2.parent = root1下标;
}在进行“并”操作时,需要获得两棵树的根结点在森林中的位置(顺序存储的下标)
仅当两棵树不一样时,才能进行“并”操作,将一棵树的父结点记为另一棵树的根结点。
3 “并”操作的优化
为了让每一次“并”操作都是让小树“并”到大树上,可以用根结点的绝对值来表示树中结点总数
4 “查”操作的优化(压缩路径)
先用原来的“查”操作找到根结点,随后将查找路径上的所有结点挂到根节点上。这就是压缩路径,核心思想是使树尽可能变矮。
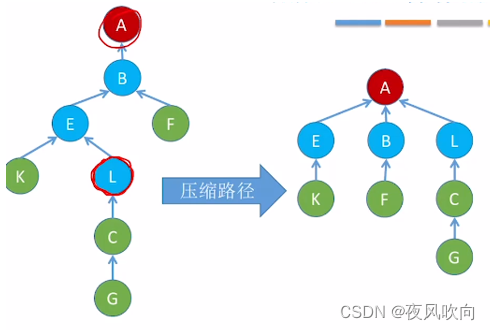
5 小结
不想打字了,就这样对着看了。注意:此处的Union函数是将结点x、y所属集合进行合并,所以需要先找到其所在集合的根结点,所以在“并”操作之前需要进行“查”操作。

并查集中的树需要经过“并”操作进行合成,优化“并”操作后,最坏情况下树的高度为
当采用压缩路径的方式优化“查”操作后,查的次数越多,树的高度越低,甚至会出现仅有2层高的树。
后记
过两天就要准备毕设答辩了,又有的忙了。
明天开始复习图,图开始才是难点啊,我去翻翻考纲,看看能不能挑重点。
看完了数据结构再去回顾一下参考教材,看看哪里还有遗漏。
暂时就这些。






















 215
215











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








