基尔霍夫电压定律和基尔霍夫电流定律的深入解析及应用

一、背景描述

1845年，德国物理学家Gustav Robert Kirchhoff提出了基尔霍夫定律，包括基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）。基尔霍夫定律是电路理论的基础，适用于分析复杂电路中的电流和电压关系。该定律不仅应用于直流电路，也适用于低频交流电路和含有电子元件的非线性电路。在现代电路理论中，基尔霍夫定律为分析和设计电路提供了强有力的工具。

基尔霍夫定律在电路分析中的作用是提供了一种系统化的方法来分析和计算复杂电路中的电流和电压分布。以下是对基尔霍夫定律在电路分析中作用的详细阐述：

1. 节点电流分析

   • 电流守恒性：KCL基于电荷守恒原理，确保了在任何给定节点上，流入节点的总电流等于流出节点的总电流。这是电路分析中的基本出发点，对于理解和计算电路中各节点的电流至关重要。
   • 方程建立：利用KCL，可以为电路中的每个节点建立一个电流方程。这些方程反映了节点处电流的守恒关系，是求解电路中电流分布的基础。
   • 简化计算：通过应用KCL，可以将复杂的电路简化为一系列节点电流方程，从而更容易找到解决问题的方法。

2. 回路电压分析

   • 电压降与电动势平衡：KVL表明，在闭合回路中，所有元件上的电压降之和等于所有电动势之和。这一定律确保了电路中能量的守恒，是分析电路中电压分布的关键。
   • 方程构建：KVL允许为电路中的每个独立回路建立一个电压方程。这些方程描述了回路中电压的守恒关系，是求解电路中电压分布的基础。
   • 复杂电路简化：通过应用KVL，可以将复杂的电路简化为一系列回路电压方程，从而更容易找到解决问题的方法。

3. 联立方程求解

   • 方程组求解：在电路分析中，通常需要将KCL和KVL联合使用，形成一组联立方程。这些方程描述了电路中电流和电压的相互关系，是求解电路问题的核心。
   • 未知量确定：通过求解这些联立方程，可以确定电路中各个支路的电流和电压值，从而全面了解电路的工作状态。

4. 电路设计优化

   • 性能评估：基尔霍夫定律不仅用于分析现有电路，还可以用于评估电路的性能和安全性。通过计算电路中的电流和电压，可以预测电路的行为，并对其进行优化设计。
   • 故障诊断：在电路出现故障时，基尔霍夫定律可以帮助工程师快速定位问题所在。通过分析电路中的电流和电压分布，可以找出故障原因，并进行相应的修复。

5. 理论实践结合

   • 理论验证：基尔霍夫定律为电路理论提供了坚实的基础，通过实验验证这些定律的正确性，可以加深对电路工作原理的理解。
   • 实践指导：在实际电路设计和分析过程中，基尔霍夫定律提供了重要的指导原则。工程师可以根据这些定律来选择合适的元器件、设计合理的电路布局，并预测电路的行为。

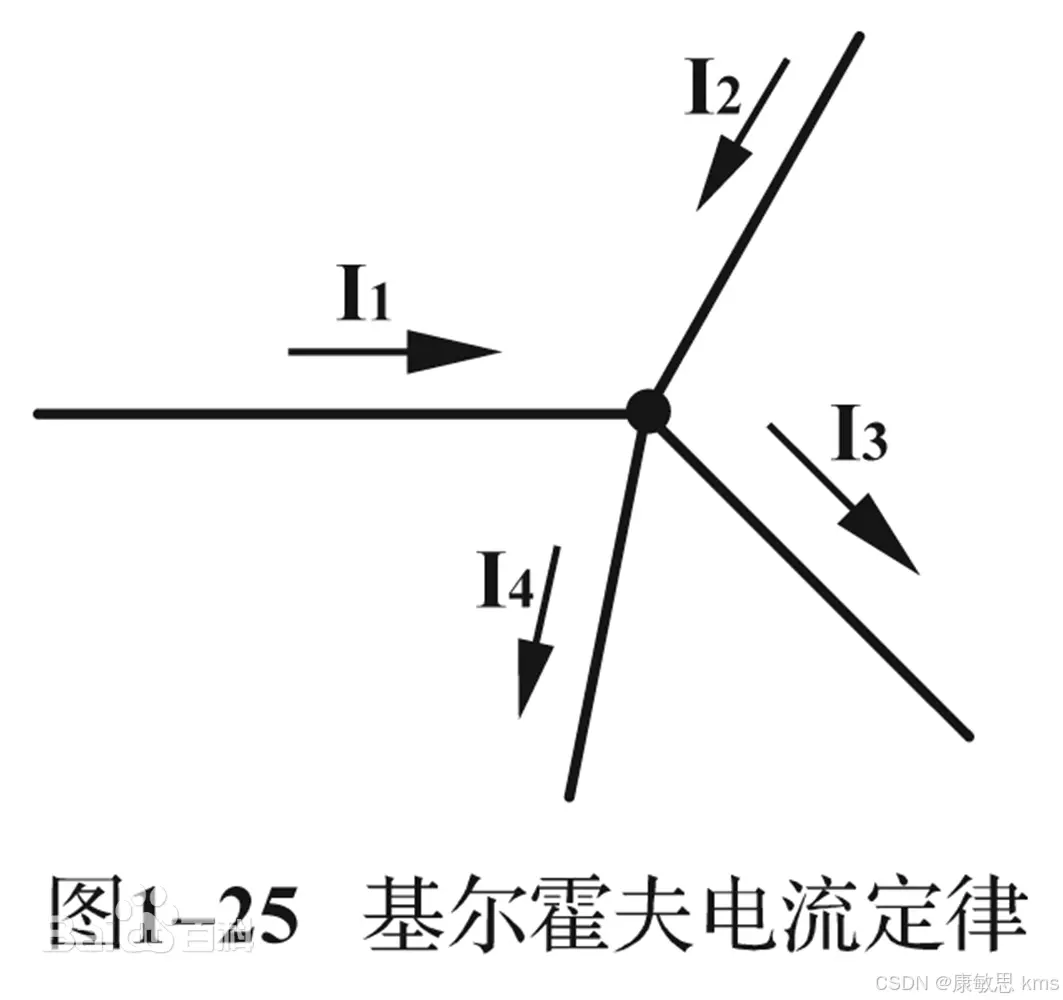
二、基尔霍夫电流定律（KCL）

1. 定义与基本概念

1.1 电流连续性原理

基尔霍夫电流定律（KCL）基于电荷守恒定律，即在一个封闭系统中，总电荷保持不变。电荷的连续性方程为：

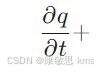
其中，q 代表电荷量，J 代表电流密度向量。

1.2 节点与支路

节点是支路的连接点，而支路则是电路中两个节点之间的电流路径。每条支路中的电流代数和为零。

1.3 广义节点

广义节点可以是任何闭合面，通过该闭合面的净电流代数和为零。这适用于电路中的任意封闭表面。

2. 数学表达式

2.1 节点电流方程

对于任意节点，流入节点的电流之和等于流出节点的电流之和：

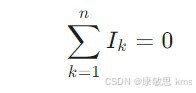
其中，Ik​ 为第 k 条支路的电流。

2.2 参考方向与正负号

电流变量前的正负号取决于电流的参考方向，通常规定参考方向指向节点的电流为负，背离节点的电流为正。

3. 应用方法

3.1 列写节点电流方程

假设某节点连接了五条支路，根据KCL，可以列出如下方程：

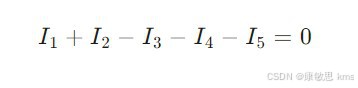
3.2 推广至封闭面

KCL还可以推广应用于电路中的任一假设封闭面。例如，选择某封闭面，使得流过该封闭面的净电流代数和为零：

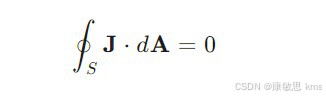
4. 实例与应用

4.1 简单电路节点分析

考虑一个简单电路，其中三个电阻器连接到一个节点，电源供电为 Is​。根据KCL，节点的电流方程为：

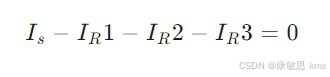
4.2 复杂电路分析

对于一个更复杂的电路，包含多个节点和支路，可以通过逐一节点列出KCL方程并求解联立方程组得到各支路电流值。

三、基尔霍夫电压定律（KVL）

1. 定义与基本概念

1.1 电场与电势

基尔霍夫电压定律（KVL）基于电场的基本性质，即电场沿任何闭合路径的线积分为零：

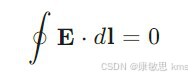
1.2 回路与网孔

回路定义为闭合的支路集合，网孔则是内部不包含任何支路的回路。KVL用于确定回路内电压之间的关系。

1.3 电动势与电压降

KVL表明沿任何闭合回路，所有元件上的电动势代数和等于所有电压降的代数和。

2. 数学表达式

2.1 回路电压方程

对于任意闭合回路，电压代数和为零：

其中，Vm​ 为第 m 个元件的电压。

2.2 绕行方向与正负号

在列写回路电压方程时，需要先选定回路绕行方向。电动势的方向与绕行方向一致时取正号，反之取负号。

3. 应用方法

3.1 回路电压方程列写

假设某回路包含四个支路电压 u1,u2,u3,u4，根据KVL，可以列出如下方程：

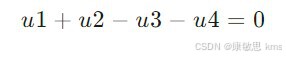
3.2 推广应用于假想回路

KVL不仅可以用于实际回路，还可以推广应用于电路中的假想回路。例如，选择某假想回路afcba，列写KVL方程：

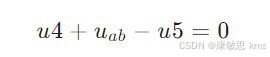
4. 实例与应用

4.1 简单回路分析

考虑一个简单回路，其中包含电阻、电源和电容，根据KVL，沿回路绕行一周，各元件电压降的代数和为零：

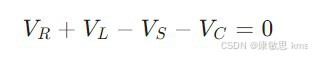
4.2 复杂回路分析

对于一个更复杂的电路，包含多个回路和支路，可以通过逐一回路列出KVL方程并求解联立方程组得到各支路电压值。例如，考虑一个桥形电路，包含四个电阻和一个电源，通过应用KVL可以得到两个独立的回路方程：

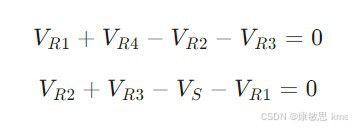
四、基尔霍夫定律的应用范围与限制

1. 适用范围

1.1 稳恒电流条件

基尔霍夫定律严格适用于稳恒电流条件下的电路分析，即电流和电压不随时间变化。

1.2 低频交流电路

由于低频交流电的电磁波长远大于电路尺度，因此可以近似认为基尔霍夫定律适用。此时，将交流电看作由许多短时间段内的稳恒直流电组成。

1.3 非线性电路分析

基尔霍夫定律不仅适用于线性电路，还可用于含有电子元件的非线性电路分析。其核心在于连接方式而非元件性质。

2. 限制与修正

2.1 含时电流的影响

当电路中含有时变电流时，如电容器的充放电过程，必须考虑位移电流。此时，传统的KVL需修正为包含位移电流项。

2.2 电感器的影响

对于含有电感器的电路，自感和互感现象会导致额外的电动势产生，必须在KVL中加入相应的感应电动势项。

2.3 能量传递问题

在某些情况下，如三端口晶体管激光器中，传统基尔霍夫定律无法直接解释光信号输出涉及的能量守恒问题。此时，需要对基尔霍夫定律进行扩展或修正，以适应新的情况。

五、总结与展望

基尔霍夫电压定律和电流定律作为电路理论的基础，提供了分析和计算复杂电路中电流和电压关系的强有力工具。随着电气技术和电子工程的发展，这些定律在直流电路、交流电路以及非线性电路的分析中发挥了重要作用。未来，随着新型电子元件的出现和电路理论的发展，基尔霍夫定律可能会面临新的挑战和修正需求，但其基本原理和应用场景将继续指导电路设计和分析的实践。亲爱的读者们，希望本文对你们理解基尔霍夫定律有所帮助。无论是初学者还是经验丰富的工程师，掌握这些基本定律都是理解和设计电路的关键。如果你有任何问题或需要进一步的解释，请随时留言讨论。