一篇文章学会滑动窗口(单调队列) 超详细解释

最新推荐文章于 2025-03-31 17:06:30 发布

原创最新推荐文章于 2025-03-31 17:06:30 发布 · 2.3k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #蓝桥杯 #数据结构

AcWing题解专栏收录该内容

70 篇文章

订阅专栏

这篇博客介绍了如何利用单调队列优化滑动窗口最大（小）值问题，将时间复杂度从O(nm)降低到O(n)。通过示例代码详细解释了单调递增和单调递减队列的实现过程，并展示了如何应用它们来解决ACWing题库中的相关问题。

朴素做法：就是两层循环外层循环每一个数内循环窗口内每一个值，这样的时间复杂度是O(nm);

这样我们就可以用 单调队列来优化可将时间复杂度降为 O(n)。

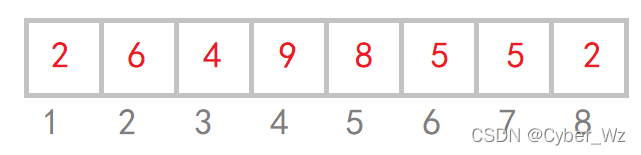
举例这是我们准备求的一个数组红色是元素值灰色是数组下标

154. 滑动窗口 - AcWing题库

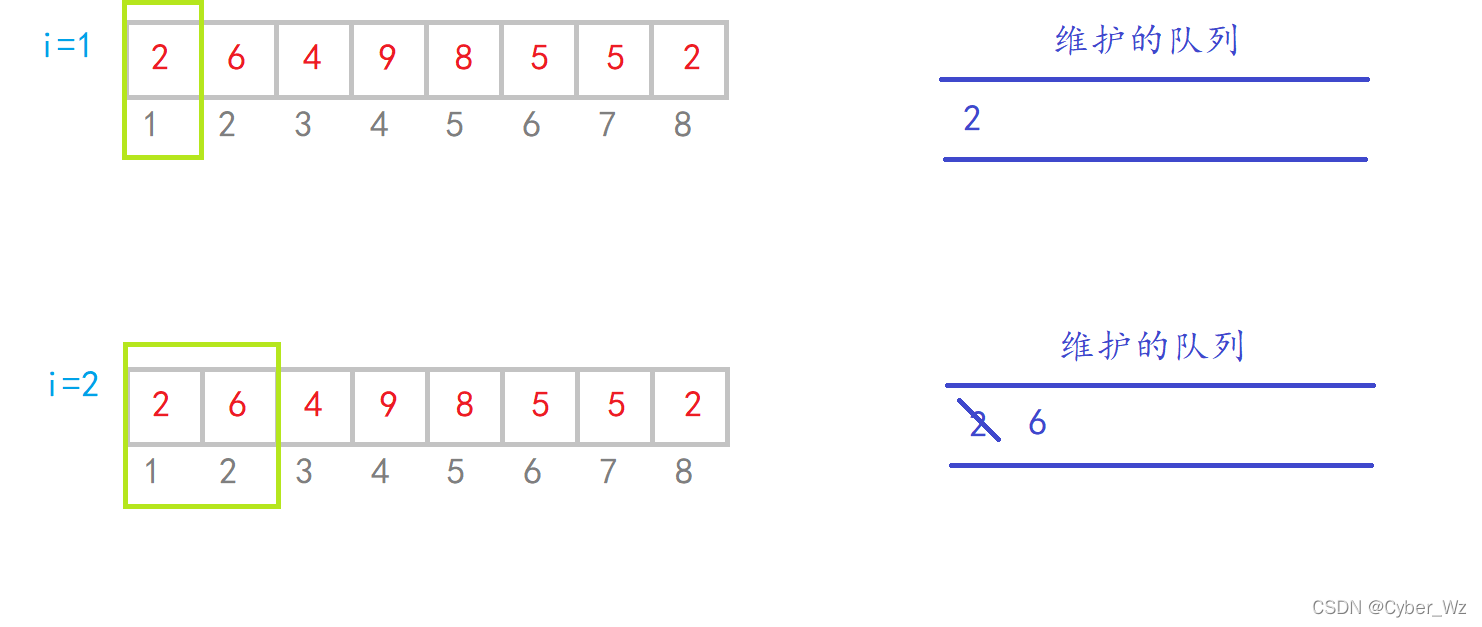
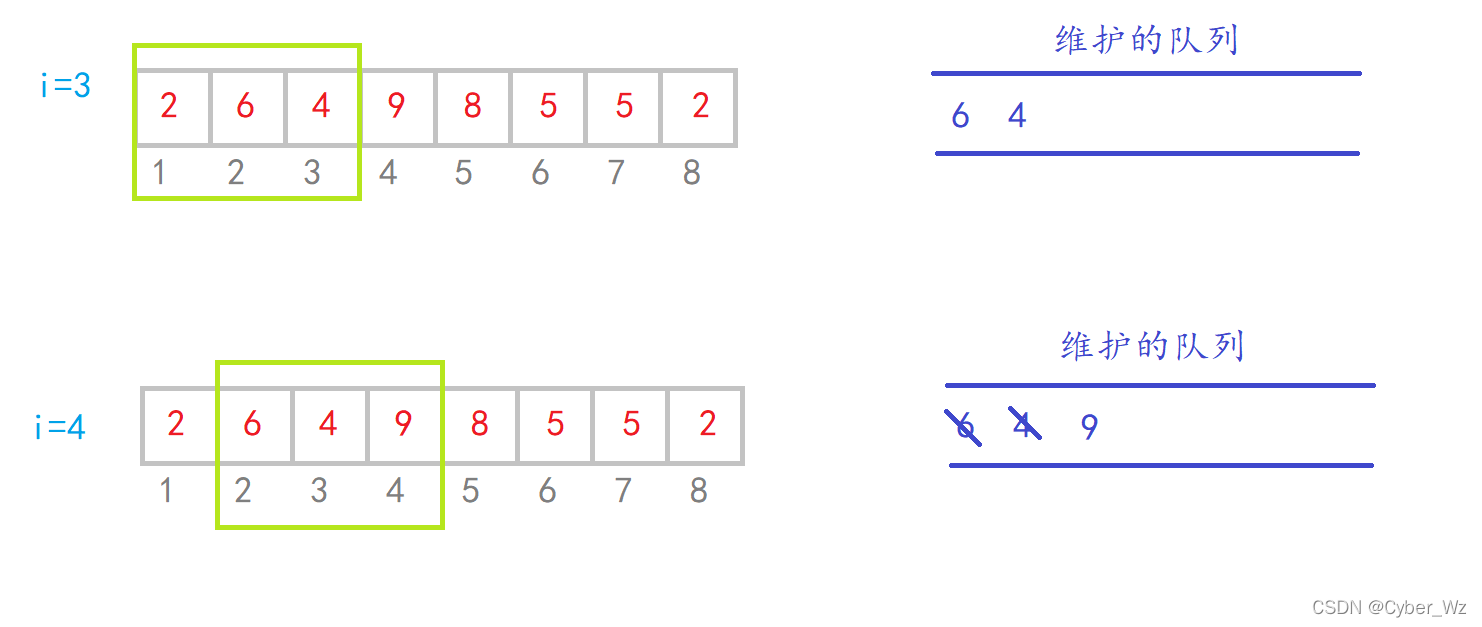
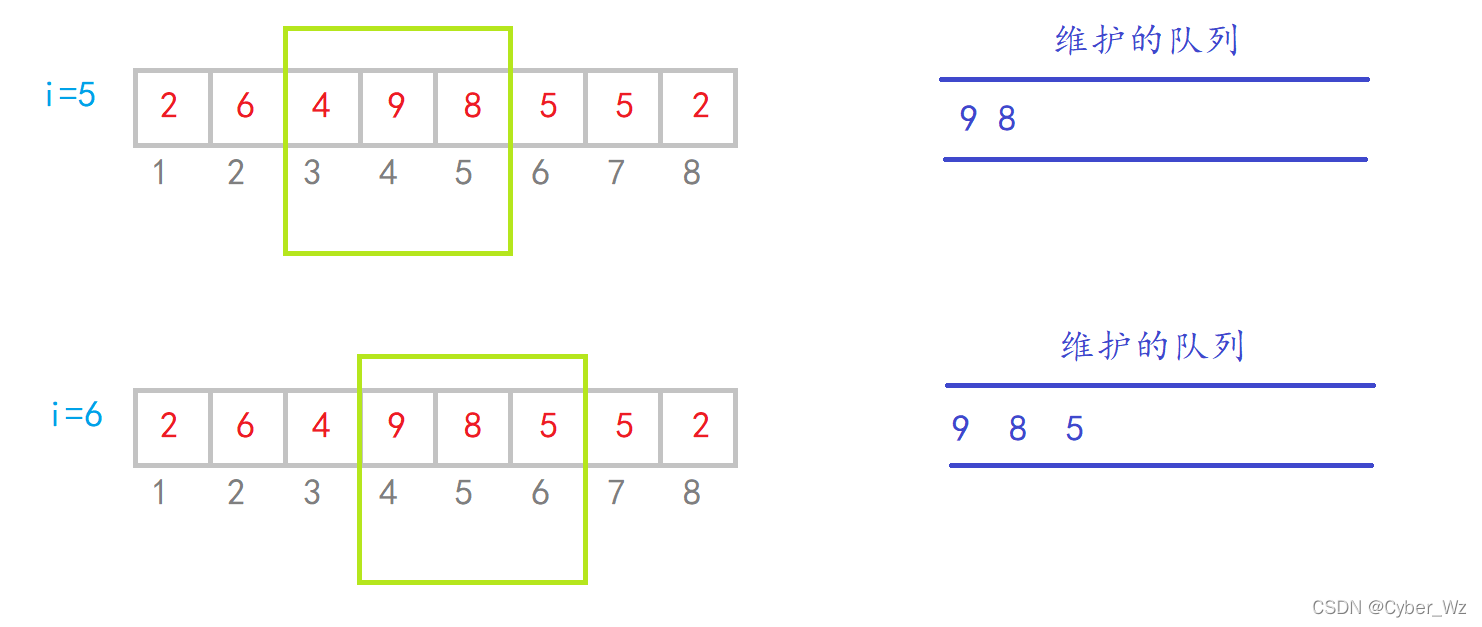
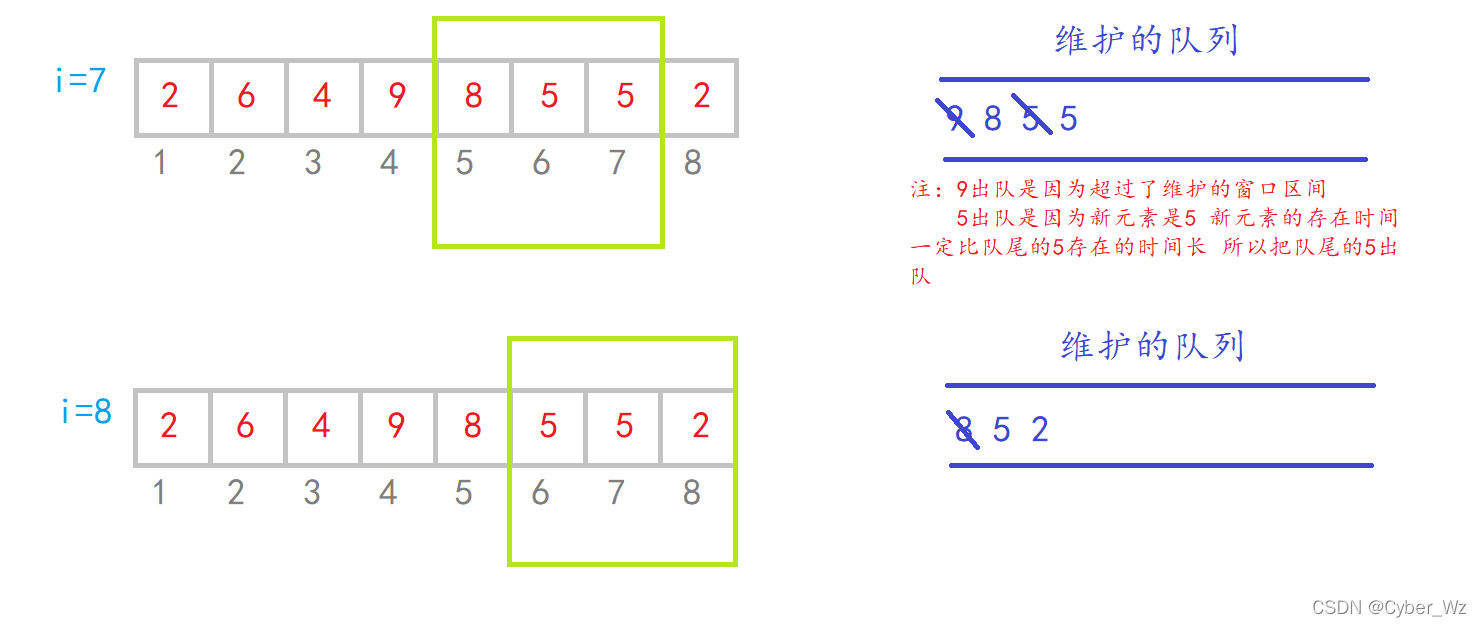
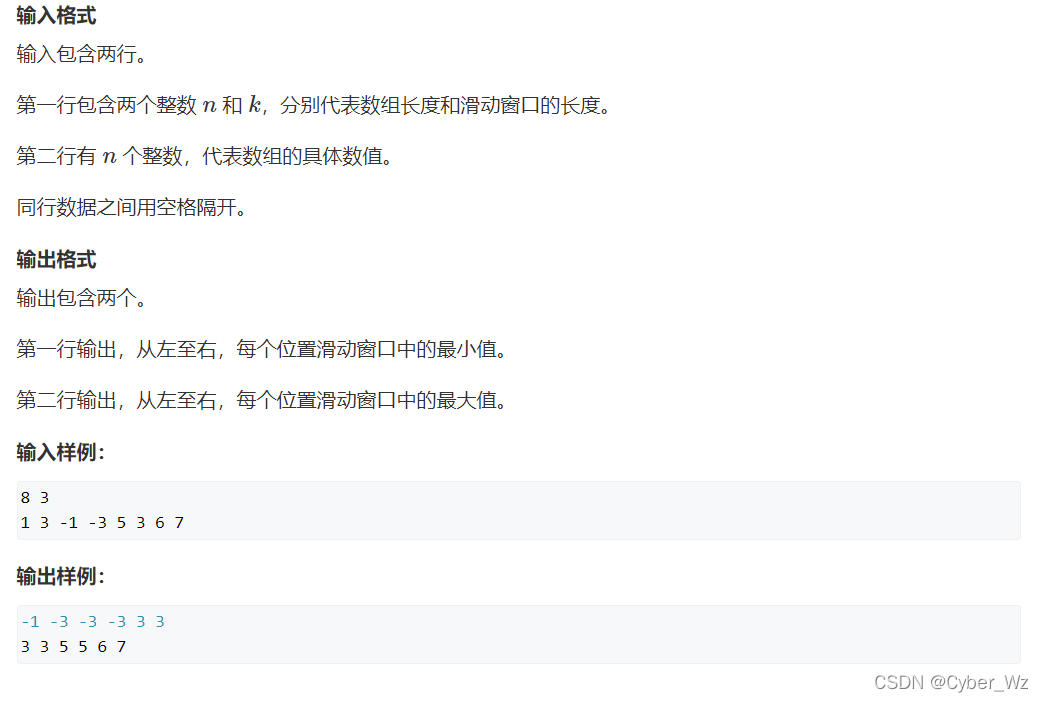
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1e6+10;

int q[N],a[N];
int n,k;

int main()
{
    cin>>n>>k;
    for (int i = 0; i < n; i ++ ) cin>>a[i];
    
    //窗口维护单调递增队列 队头为最小值
    int hh=0,tt=-1;
    for(int i = 0; i < n; i ++)
    {
        if(hh<=tt && q[hh]<i-k+1) hh++;//队头超出窗口出队 因为每次只入一个元素 所以用if即可
        while(hh<=tt && a[q[tt]]>=a[i]) tt--;//队列单调递增
        q[++tt]=i;
        //记住q里面存的是下标！！ 要输出元素应该是 a[q[hh]]
        if(i>=k-1) cout<<a[q[hh]]<<" ";//窗口内达到k个
    }
    cout<<endl;
    
    //窗口维护单调递减队列 队头为最大值
    hh=0,tt=-1;
    for(int i = 0; i < n; i ++)
    {
        if(hh<=tt && q[hh]<i-k+1) hh++;//队头超出窗口出队 因为每次只入一个元素 所以用if即可
        while(hh<=tt && a[q[tt]]<=a[i]) tt--;//队列单调递增
        q[++tt]=i;
        //记住q里面存的是下标！！ 要输出元素应该是 a[q[hh]]
        if(i>=k-1) cout<<a[q[hh]]<<" ";//窗口内达到k个
    }
    cout<<endl;
    
    return 0;
}