基于最小二乘法（牛顿迭代法求解）拟合半径已知的圆 (MATLAB)

世界尽头的青豆

已于 2024-06-26 18:02:34 修改

阅读量782

点赞数 11

文章标签：算法 matlab 最小二乘法

于 2024-06-05 16:20:03 首次发布

本文链接：https://blog.csdn.net/m0_50643362/article/details/139472298

版权

关于圆拟合的问题，目前网上大多数的做法都默认半径未知，将圆心坐标和半径都视为未知量，利用最小二乘法进行求解，从而得到圆拟合问题的解析解。但在半径已知的情况下，该算法不再适用。因此本文尝试对半径已知的圆拟合问题进行求解。

1 问题描述

已知拟合曲线为半径已知的圆弧，根据数据点集合计算得到圆心。

输入：平面上各点坐标 $(x_{i},y_{i})$ $\forall i = 1,2,...,N$ ，半径 $R$ 。

输出：圆心坐标 $(a,b)$ 。

2 理论分析

已知圆的方程为：

$(x-a)^2+(y-b)^2=R^2$

对于各数据点，令：

$g(x_i,y_i,a,b)=x_i^2+y_i^2-2ax_i-2by_i+a^2+b^2-R^2,\ \ \forall i=1,2,\ldots,N$

令：

$f(a,b)=\sum_{i=1}^{N}{g(x_i,y_i,a,b)^2}$

则原问题转为问题转化为下述优化问题：

$\underset{a,b}{\text{min}} \, f(a,b)$

$f(a,b)$ 取得最小值的必要条件如下：

$\frac{\partial f\left(a,b\right)}{\partial a}=\sum_{i=1}^{N}\frac{\partial g\left(x_i,y_i,a,b\right)}{\partial a}=-\sum_{i=1}^{N}4g\left(x_i,y_i,a,b\right)\left(a-x_i\right)=0$

$\frac{\partial f\left(a,b\right)}{\partial b}=\sum_{i=1}^{N}\frac{\partial g\left(x_i,y_i,a,b\right)}{\partial b}=-\sum_{i=1}^{N}4g\left(x_i,y_i,a,b\right)\left(b-y_i\right)=0$

（但不为充分条件，因为圆心相对于圆弧的对侧一定存在至少一个极值点）

即满足下列方程组的解 $(a,b)$ :

$h_1\left(a,b\right)=\sum_{i=1}^{N}g\left(x_i,y_i,a,b\right)\left(a-x_i\right)=0$

$h_2\left(a,b\right)=\sum_{i=1}^{N}g\left(x_i,y_i,a,b\right)\left(b-y_i\right)=0$

即为圆心坐标的值。这个方程组可能没有解析解，可用牛顿迭代法求解上述问题。（牛顿迭代法的初值应该位于圆心这一侧，否则可能会收敛至错误的值）

牛顿迭代法参考：Matlab--用最小二乘法确定指数函数的系数(牛顿法解二元非线性方程组）

对于该问题，有：

$h\left(a,b\right)\approx\ h\left(a_0,b_0\right)+\frac{\partial h\left(a_0,b_0\right)}{\partial a}\left(a-a_0\right)+\frac{\partial h\left(a_0,b_0\right)}{\partial b}\left(b-b_0\right)$

得到：

$h_1\left(a_0,b_0\right)+\frac{\partial h_1(a_0,b_0)}{\partial a}(a-a_0)+\frac{\partial h_1(a_0,b_0)}{\partial b}(b-b_0)=0$

$h_2\left(a_0,b_0\right)+\frac{\partial h_2(a_0,b_0)}{\partial a}(a-a_0)+\frac{\partial h_2(a_0,b_0)}{\partial b}(b-b_0)=0$

即：

$C\left[\begin{matrix}a\\b\\\end{matrix}\right]+D=0$

其中：

$C=\left[\begin{matrix}\frac{\partial h_1(a_0,b_0)}{\partial a}&\frac{\partial h_1(a_0,b_0)}{\partial b}\\\frac{\partial h_2(a_0,b_0)}{\partial a}&\frac{\partial h_2(a_0,b_0)}{\partial b}\\\end{matrix}\right]$

$D=\left[\begin{matrix} h_1 (a_0,b_0)-\frac{\partial h_1(a_0,b_0)}{\partial a} a_0-\frac{\partial h_1(a_0,b_0)}{\partial b} b_0\\h_2(a_0,b_0)-\frac{\partial h_2(a_0,b_0)}{\partial a} a_0-\frac{\partial h_2 (a_0,b_0)}{\partial b} b_0\\\end{matrix}\right]$

解得：

$\left[\begin{matrix}a\\b\\\end{matrix}\right]=\ -C^{-1}D$

按照牛顿迭代法步骤迭代即可得到估计解。

3 偏导数计算

对于该问题，函数及其偏导数计算如下：

$\begin{array}{rl} &h_1\left(a,b\right)=\sum_{i=1}^{N}g\left(x_i,y_i\right)\left(a-x_i\right) \\ &h_2\left(a,b\right)=\sum_{i=1}^{N}g\left(x_i,y_i\right)\left(b-y_i\right)\\ &\frac{\partial h_1\left(a,b\right)}{\partial a}=\sum_{i=1}^{N}{\left(2a-2x_i\right)\left(a-x_i\right)+g\left(x_i,y_i\right)}\\ &\frac{\partial h_1\left(a,b\right)}{\partial b}=\sum_{i=1}^{N}\left(2b-2y_i\right)\left(a-x_i\right)\\&\frac{\partial h_2\left(a,b\right)}{\partial a}=\sum_{i=1}^{N}\left(2a-2x_i\right)\left(b-y_i\right)\\&\frac{\partial h_2\left(a,b\right)}{\partial b}=\sum_{i=1}^{N}{\left(2b-2y_i\right)\left(b-y_i\right)+g\left(x_i,y_i\right)}\end{array}$

记：

$U_x=\sum_{i=1}^{N}x_i\ \ \ \ \ U_y=\sum_{i=1}^{N}y_i\ \ \ \ \ \ U_{xx}=\sum_{i=1}^{N}x_i^2\ \ \ \ \ U_{yy}=\sum_{i=1}^{N}y_i^2$

$U_{xy}=\sum_{i=1}^{N}{x_iy_i}\ \ \ U_{xxx}=\sum_{i=1}^{N}x_i^3\ \ U_{yyy}=\sum_{i=1}^{N}y_i^3$

$U_{xyy}=\sum_{i=1}^{N}{x_iy_i^2}\ \ \ U_{xxy}=\sum_{i=1}^{N}{x_i^2y_i}$

有：

$\begin{array}{rl} h_{1}(a, b) =& -U_{x x x}-U_{x y y}+3 a U_{x x}+a U_{y y}+2 b U_{x y}+\left(R^{2}-3 a^{2}-b^{2}\right) U_{x} \\ & -2 a b U_{y}+N a^{3}+N a b^{2}-N a R^{2}\\h_2\left(a,b\right)=&-U_{yyy}-U_{xxy}+bU_{xx}+3bU_{yy}+2aU_{xy}-2abU_x\\&+\left(R^2-3b^2-a^2\right)U_y+Na^2b+Nb^3-NbR^2\\\frac{\partial h_1\left(a,b\right)}{\partial a}=&3U_{xx}+U_{yy}-6aU_x-2bU_y+3Na^2+Nb^2-NR^2 \\\frac{\partial h_1\left(a,b\right)}{\partial b}=&\frac{\partial h_2\left(a,b\right)}{\partial a}\\=&2U_{xy}-2bU_x-2aU_y+2Nab\\ \frac{\partial h_2\left(a,b\right)}{\partial b}=&U_{xx}+3U_{yy}-2aU_x-6bU_y+Na^2+3Nb^2-NR^2 \end{array}$

4 仿真

采用MATLAB仿真，设真实圆心坐标为 $(50,30)$ ，半径为 $3.5$ ，输入坐标点坐标存在随机噪声，大小为 $-0.5\sim 0.5$ 。牛顿迭代初值为 $(0,0)$ ，容许误差为 $1\times {10}^{-10}$ ，最大迭代次数为 $100$ 。

输出结果如下：

迭代次数:1
当前圆心估计坐标为:[0,0]
迭代次数:2
当前圆心估计坐标为:[17.1563,10.7807]
迭代次数:3
当前圆心估计坐标为:[28.5949,17.9486]
迭代次数:4
当前圆心估计坐标为:[36.2223,22.6982]
迭代次数:5
当前圆心估计坐标为:[41.31,25.8203]
迭代次数:6
当前圆心估计坐标为:[44.7063,27.8337]
迭代次数:7
当前圆心估计坐标为:[46.9776,29.0716]
迭代次数:8
当前圆心估计坐标为:[48.4997,29.7422]
迭代次数:9
当前圆心估计坐标为:[49.5029,29.9978]
迭代次数:10
当前圆心估计坐标为:[50.0634,30.0456]
迭代次数:11
当前圆心估计坐标为:[50.2302,30.0637]
迭代次数:12
当前圆心估计坐标为:[50.2434,30.0666]
迭代次数:13
当前圆心估计坐标为:[50.2435,30.0667]
迭代次数:14

拟合结果图如下。其中，蓝色点为随机干扰下的位于圆弧上的点云，蓝色X所在位置为真实圆心坐标。红线为已知半径的圆拟合结果，红色X所在位置为已知半径的圆心估计坐标；粉线为半径未知的最小二乘法拟合结果，粉色X所在位置为半径未知的最小二乘法圆心估计坐标。

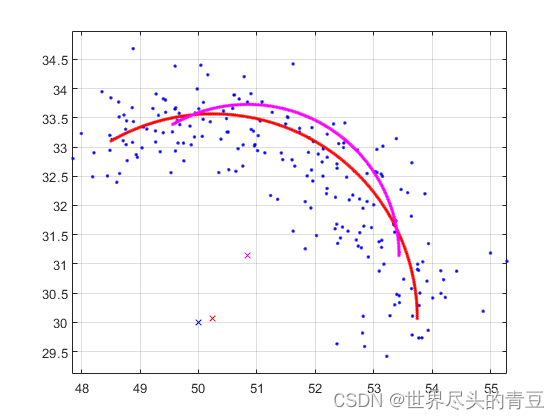
圆心估计结果如下：

圆心实际坐标为：[50,30]
实际半径为:3.5
牛顿迭代法圆心估计坐标为：[50.2435,30.0667]
牛顿迭代法圆心估计误差为：0.25242
最小二乘法圆心估计坐标为：[50.845,31.1428]
最小二乘法估计半径为:2.5861
最小迭代法圆心估计误差为：1.4213

可以看出该算法较好地利用了半径信息进行拟合。

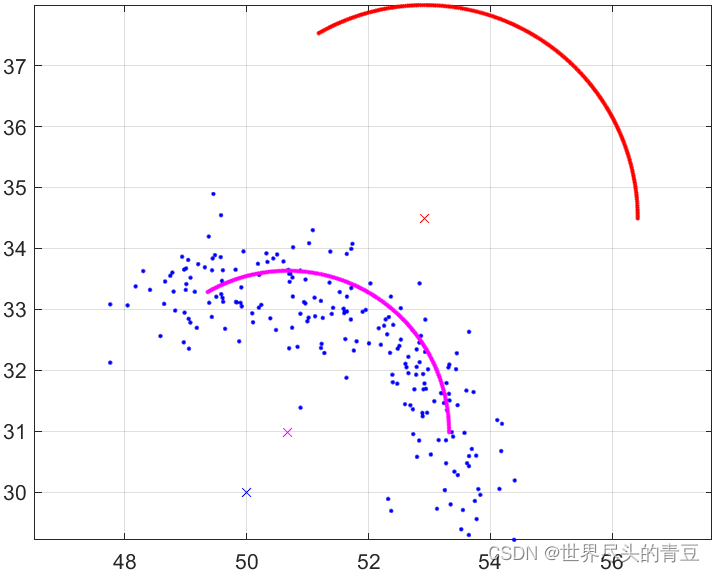
更改牛顿迭代法初值为 $(100,100)$ ，得到拟合结果如下图，可以看到，圆心收敛到圆外的错误位置，这是因为建立的优化问题存在多个极值点的缘故。因此实际使用时，需要通过一些信息得到圆心初始位置，或者根据圆弧上点的坐标，往多个方向设定初始值，分别迭代计算，取最终的最小值。

5 代码

算法主要代码如下：

%% 牛顿迭代法求解固定半径圆心坐标
Ux = sum(x);
Uy = sum(y);
Uxx = sum(x.^2);
Uyy = sum(y.^2);
Uxy = sum(x.*y);
Uxxx = sum(x.^3);
Uyyy = sum(y.^3);
Uxxy = sum(x.^2.*y);
Uxyy = sum(x.*y.^2);
N = length(x);

U = [Ux,Uy,...
    Uxx,Uyy,Uxy,...
    Uxxx,Uyyy,Uxxy,Uxyy];

iterNum = 100;
ruslutErrorMax = 1e-10;
% 圆心初值需在圆弧的内侧，否则可能会收敛到错误的位置
% 实际使用时，需要通过一些信息得到圆心初始位置
% 或者根据圆弧上点的坐标，往多个方向设定初始值，分别迭代计算，取最终的最小值
a0 = 0;
b0 = 0;

for i = 1:iterNum
    disp(strcat(['迭代次数:',num2str(i)]));
    disp(strcat(['当前圆心估计坐标为:[',num2str(a0),',',num2str(b0),']']));
    [h1,dh1_da,dh1_db] = fun_h1(a0,b0,R_real,U,N);
    [h2,dh2_da,dh2_db] = fun_h2(a0,b0,R_real,U,N);
    C = [dh1_da,dh1_db;
        dh2_da,dh2_db];
    D = [h1-dh1_da*a0-dh1_db*b0;
        h2-dh2_da*a0-dh2_db*b0];
    result = -C\D;
    a_newton = result(1);
    b_newton = result(2);
    if abs(a_newton-a0) + abs(b_newton-b0) < ruslutErrorMax
        break;
    end
    a0 = a_newton;
    b0 = b_newton;
end

全部代码如下：

clear;close all;clc;

t=0:0.01:pi*2/3;
a_real=50;
b_real=30;
R_real=3.5;
R_uncertainty = 0.5;
x=a_real+R_real*cos(t)+R_uncertainty*randn(1,length(t));
y=b_real+R_real*sin(t)+R_uncertainty*randn(1,length(t));

%% 牛顿迭代法求解固定半径圆心坐标
Ux = sum(x);
Uy = sum(y);
Uxx = sum(x.^2);
Uyy = sum(y.^2);
Uxy = sum(x.*y);
Uxxx = sum(x.^3);
Uyyy = sum(y.^3);
Uxxy = sum(x.^2.*y);
Uxyy = sum(x.*y.^2);
N = length(x);

U = [Ux,Uy,...
    Uxx,Uyy,Uxy,...
    Uxxx,Uyyy,Uxxy,Uxyy];

iterNum = 100;
ruslutErrorMax = 1e-10;
% 圆心初值需在圆弧的内侧，否则可能会收敛到错误的位置
% 实际使用时，需要通过一些信息得到圆心初始位置
% 或者根据圆弧上点的坐标，往多个方向设定初始值，分别迭代计算，取最终的最小值
a0 = 0;
b0 = 0;

for i = 1:iterNum
    disp(strcat(['迭代次数:',num2str(i)]));
    disp(strcat(['当前圆心估计坐标为:[',num2str(a0),',',num2str(b0),']']));
    [h1,dh1_da,dh1_db] = fun_h1(a0,b0,R_real,U,N);
    [h2,dh2_da,dh2_db] = fun_h2(a0,b0,R_real,U,N);
    C = [dh1_da,dh1_db;
        dh2_da,dh2_db];
    D = [h1-dh1_da*a0-dh1_db*b0;
        h2-dh2_da*a0-dh2_db*b0];
    result = -C\D;
    a_newton = result(1);
    b_newton = result(2);
    if abs(a_newton-a0) + abs(b_newton-b0) < ruslutErrorMax
        break;
    end
    a0 = a_newton;
    b0 = b_newton;
end

%% 最小二乘法求解未知半径圆心坐标
x=x(:); % Transpose
y=y(:); 
Mole=[x y ones(size(x))];
Deno=-(x.^2+y.^2);
Result1=Mole\Deno;
% x^2+y^2+ax+by+c=0 ---> ax+by+c=-(x^2+y^2)
% [x y 1]*[a;b;c]=-(x^2+y^2)
% [a;b;c]=[x y 1]\[-(x^2+y^2)]
% Column principal elimination method
% Least square fitting can also be used
m=[x y ones(size(x))]\Deno; 
a_ls=-0.5*m(1);
b_ls=-0.5*m(2);
R_ls=sqrt((m(1)^2+m(2)^2)/4-m(3));


%% 结果显示
figure
plot(a_real,b_real,'xb',x,y,'b.');
hold on;
plot(a_newton,b_newton,'xr',(a_newton+R_real*cos(t)),(b_newton+R_real*sin(t)),'r.');
hold on;
plot(a_ls,b_ls,'xm',(a_ls+R_ls*cos(t)),(b_ls+R_ls*sin(t)),'m.');
grid on;
axis equal;

disp(strcat(['圆心实际坐标为：[',num2str(a_real),',',num2str(b_real),']']));
disp(strcat(['实际半径为:',num2str(R_real)]));
disp(strcat(['牛顿迭代法圆心估计坐标为：[',num2str(a_newton),',',num2str(b_newton),']']));
disp(strcat(['牛顿迭代法圆心估计误差为：',num2str(sqrt((a_newton-a_real)^2+(b_newton-b_real)^2))]));

disp(strcat(['最小二乘法圆心估计坐标为：[',num2str(a_ls),',',num2str(b_ls),']']));
disp(strcat(['最小二乘法估计半径为:',num2str(R_ls)]));
disp(strcat(['最小迭代法圆心估计误差为：',num2str(sqrt((a_ls-a_real)^2+(b_ls-b_real)^2))]));

其中fun_f1和fun_f2定义为：

function [y,dy_da,dy_db] = fun_h1(a,b,R,U,N)
    U_cell = num2cell(U);
    [Ux,Uy,...
    Uxx,Uyy,Uxy,...
    Uxxx,Uyyy,Uxxy,Uxyy] = deal(U_cell{:});
    y = -Uxxx-Uxyy...
        +3*a*Uxx+a*Uyy+2*b*Uxy...
        +(R^2-3*a^2-b^2)*Ux-2*a*b*Uy...
        +N*a^3+N*a*b^2-N*a*R^2;
    dy_da = 3*Uxx+Uyy...
        -6*a*Ux-2*b*Uy...
        +3*N*a^2+N*b^2-N*R^2;
    dy_db = 2*Uxy...
        -2*b*Ux-2*a*Uy...
        +2*N*a*b;
end

function [y,dy_da,dy_db] = fun_h2(a,b,R,U,N)
    U_cell = num2cell(U);
    [Ux,Uy,...
    Uxx,Uyy,Uxy,...
    Uxxx,Uyyy,Uxxy,Uxyy] = deal(U_cell{:});
    y = -Uyyy-Uxxy...
        +b*Uxx+3*b*Uyy+2*a*Uxy...
        -2*a*b*Ux+(R^2-3*b^2-a^2)*Uy...
        +N*a^2*b+N*b^3-N*b*R^2;
    dy_da = 2*Uxy...
        -2*b*Ux-2*a*Uy...
        +2*N*a*b;
    dy_db = Uxx+3*Uyy...
        -2*a*Ux-6*b*Uy...
        +N*a^2+3*N*b^2-N*R^2;
end

世界尽头的青豆

关注

11
点赞
踩
30

收藏

觉得还不错? 一键收藏
0
评论
基于最小二乘法（牛顿迭代法求解）拟合半径已知的圆 (MATLAB)

关于圆拟合的问题，目前网上大多数的做法都默认半径未知，将圆心坐标和半径都视为未知量，利用最小二乘法进行求解，从而得到圆拟合问题的解析解。但在半径已知的情况下，该算法不再适用。因此本文尝试对半径已知的圆拟合问题进行求解。
复制链接

扫一扫