网络流(最大流,dininc,费用流,上下界网络流)

8aceMaker

已于 2022-09-07 21:23:08 修改

阅读量483

点赞数 1

分类专栏：图论文章标签：图论算法 c++

于 2022-07-11 16:11:47 首次发布

本文链接：https://blog.csdn.net/m0_51028279/article/details/125664252

版权

图论专栏收录该内容

10 篇文章 0 订阅

订阅专栏

最大流EK算法： $O(nm^2)$

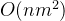
struct EK_maxflow{
    const int nn;
    vector<int> vis,pre;
    vector<vector<int>> mp;
    EK_maxflow(int n1,vector<vector<int>> &mp1):nn(n1),vis(n1+1),pre(n1+1),mp(mp1){};
    void update_edge(int u,int flow)
    {
        while(pre[u]!=-1)
        {
            mp[pre[u]][u]-=flow;
            mp[u][pre[u]]+=flow;
            u=pre[u];
        }
    }
    int find_path_bfs(int st,int end)
    {
        fill(vis.begin(),vis.end(),0);
        fill(pre.begin(),pre.end(),-1);
        vis[st]=1;
        int mi=inf;
        queue<int> q;
        q.push(st);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            if(u==end)
                break;
            for(int i=1;i<=nn;i++)
            {
                if(!vis[i]&&mp[u][i]!=0)
                {
                    q.push(i);
                    vis[i]=1;
                    mi=(mi<mp[u][i]?mi:mp[u][i]);
                    pre[i]=u;
                }
            }
        }
        if(pre[end]==-1)
            return 0;
        else
            return mi;
    }
    int Max_flow(int st,int end)
    {
        int max_flow=0;
        while(1)
        {
            int new_flow=find_path_bfs(st,end);
            update_edge(end,new_flow);
            max_flow+=new_flow;
            if(!new_flow)
                return max_flow;
        }
    }
};

Dinic算法: $O(n^2m)$

struct dinic{
    const int nn;
    int INF = inf*inf;
    struct Edge{
        int to,cap;
        Edge(int to,int cap):to(to),cap(cap){}
    };
    vector<int> dis,cur;
    vector<Edge> e;
    vector<vector<int>> g;
    dinic(int n1):nn(n1),dis(n1+1),cur(n1+1),g(n1+1){}
    void add(int u,int v,int w)
    {
        g[u].emplace_back(e.size());
        e.emplace_back(v,w);
        g[v].emplace_back(e.size());
        e.emplace_back(u,0);
    }
    bool bfs(int st,int end)
    {
        fill(dis.begin(),dis.end(),-1);
        dis[st]=0;
        queue<int> q;
        q.push(st);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            for(int i:g[u])
            {
                auto [v,w]=e[i];
                if(dis[v]==-1&&w>0)
                {
                    q.push(v);
                    dis[v]=dis[u]+1;
                }
            }
        }
        return dis[end]!=-1;//若不可以到终点（起点）就返回false 
    }
    int dfs(int st,int end,int flo)//dfs就是求节点u在残量为flo时的最大增量
    {
        if(st==end)
            return flo;
        int delta=flo;
        for(int i=cur[st];i<g[st].size();i++)
        {
            int j=g[st][i];
            auto [v,w]=e[j];
            cur[st]=i;
            if((dis[v]==dis[st]+1)&&w>0)
            {
                int d=dfs(v,end,min(delta,w));
                e[j].cap-=d;
                e[j^1].cap+=d;
                delta-=d;
                if(delta==0)
                    break;
            }
        }
        return flo-delta;
    }
    int max_flow(int st,int end)
    {
        int maxflow=0;
        while(bfs(st,end))
        {
            fill(cur.begin(),cur.end(),0);
            maxflow+=dfs(st,end,INF);
        }
        return maxflow;
    }
};

HLPP算法 $O(n^2\sqrt m)$

#define Cap int
struct HLPP {
    struct Edge {
        int j, q;
        Cap x;
    };
    int N, K = 0, m = 0, cnt = 0;
    vector<vector<Edge>> G;
    vector<int> H, p1;
    vector<Cap> X;
    vector<vector<int>> Q;
    HLPP(int nn): N(nn), G(N), H(N), p1(N), X(N), Q(N * 2 + 1) {}
    void addEdge(int i, int j, Cap x, Cap y = 0) {
        int p = G[i].size(), q = G[j].size();
        G[i].push_back({j, q, x});
        G[j].push_back({i, p, y});
    }
    void push(int i) {
        Q[H[i]].push_back(i);
        m = max(m, H[i]);
    }
    void relabel(int t) {
        cnt = 0;

        for (auto &q : Q)
            q.clear();

        fill(H.begin(), H.end(), N * 2 + 1);

        vector<int> Q(N);
        int s = -1, e = -1;
        H[Q[++e] = t] = 0;

        while (s < e) {
            int i = Q[++s], h = H[i] + 1;

            for (auto&[j, q, x] : G[i])
                if (G[j][q].x && h < H[j]) {
                    H[Q[++e] = j] = h;

                    if (X[j] > 0)
                        push(j);
                }
        }
    }
    void discharge(int i) {
        auto &v = X[i];
        int h = N * 2;

        for (int &p = p1[i], m = G[i].size(); m--; p = (p ? : G[i].size()) - 1) {
            auto&[j, q, x] = G[i][p];

            if (!x)
                continue;

            if (H[i] != H[j] + 1) {
                h = min(h, H[j] + 1);
                continue;
            }

            auto f = min(x, v);
            x -= f, v -= f;

            if (!X[j])
                push(j);

            X[j] += f, G[j][q].x += f;

            if (!v)
                return;
        }

        cnt++;
        H[i] = h;

        if (H[i] < N && X[i] > 0)
            push(i);
    }
    Cap calc(int s, int t, Cap inf = numeric_limits<Cap>::max()) {
        relabel(t);
        X[s] = inf, X[t] = -inf;
        push(s);

        for (; ~m; m--)
            while (Q[m].size()) {
                int i = Q[m].back();
                Q[m].pop_back();

                if (H[i] == m)
                    discharge(i);

                if (cnt >= 4 * N)
                    relabel(t);
            }

        return X[t] + inf;
    }
};

c++98 dinic

struct dinic{
    const int nn,INF;
    struct Edge{
        int to,cap;
        Edge(int to,int cap):to(to),cap(cap){}
    };
    vector<int> dis,cur;
    vector<Edge> e;
    vector<vector<int> > g;
    dinic(int n1):nn(n1),INF(inf),dis(n1+1),cur(n1+1),g(n1+1){}
    void add(int u,int v,int w)
    {
        g[u].push_back(e.size());
        e.push_back({v,w});
        g[v].push_back(e.size());
        e.push_back({u,0});
    }
    bool bfs(int st,int end)
    {
        fill(dis.begin(),dis.end(),-1);
        dis[st]=0;
        queue<int> q;
        q.push(st);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            for(int kk=0;kk<g[u].size();kk++)
            {
                int i=g[u][kk];
                int v=e[i].to,w=e[i].cap;
                if(dis[v]==-1&&w>0)
                {
                    q.push(v);
                    dis[v]=dis[u]+1;
                }
            }
        }
        return dis[end]!=-1;//若不可以到终点（起点）就返回false 
    }
    int dfs(int st,int end,int flo)//dfs就是求节点u在残量为flo时的最大增量
    {
        if(st==end)
            return flo;
        int delta=flo;
        for(int i=cur[st];i<g[st].size();i++)
        {
            int j=g[st][i];
            int v=e[j].to,w=e[j].cap;
            cur[st]=i;
            if((dis[v]==dis[st]+1)&&w>0)
            {
                int d=dfs(v,end,min(delta,w));
                e[j].cap-=d;
                e[j^1].cap+=d;
                delta-=d;
                if(delta==0)
                    break;
            }
        }
        return flo-delta;
    }
    int max_flow(int st,int end)
    {
        int maxflow=0;
        while(bfs(st,end))
        {
            fill(cur.begin(),cur.end(),0);
            maxflow+=dfs(st,end,INF);
        }
        return maxflow;
    }
};

费用流c++14

/*
 author:wuzx
 */

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<utility>
#include<string>
#include<queue>
#include<map>
#include<set>
#include<iterator>
#include<iomanip>
#include<stack>
#include<cstdio>
#define ll long long
#define int long long
#define endl "\n"
#define P pair<int,int>
#define f first
#define s second
using namespace std;
typedef unsigned long long ull;
const int maxn=110;
const int inf=0x3f3f3f3f;
const int mod=998244353;
struct MCMF{
    const int INF,nn;
    vector<tuple<int,int,int> > e;
    vector<vector<int> > g;
    vector<int> prev,h;
    MCMF(int n1):nn(n1),INF(inf),g(n1+1),prev(n1+1),h(n1+1){};
    void add_edge(int u,int v,int w,int cost)
    {
        if(u==v)
            return;
        g[u].emplace_back(e.size());
        e.emplace_back(v,w,cost);
        g[v].emplace_back(e.size());
        e.emplace_back(u,0,-cost);
    }
    bool dij(int st,int end)//mlogm 正边权
    {
        fill(prev.begin(),prev.end(),-1);
        vector<int> dis(nn+1,INF);
        dis[st]=0;
        priority_queue<P,vector<P>,greater<P> >q;
        q.emplace(0,st);
        while(!q.empty())
        {
            auto [du,u]=q.top();
            q.pop();
            if(dis[u]!=du)
                continue;
            for(int i:g[u])
            {
                auto [v,w,c]=e[i];
                c+=h[u]-h[v];
                if(w>0&&dis[v]>dis[u]+c)
                {
                    dis[v]=dis[u]+c;
                    prev[v]=i;
                    q.emplace(dis[v],v);
                }
            }
        }
        for(int i=1;i<=nn;i++)
        {
            if((h[i]+=dis[i])>=INF)
                h[i]=INF;
        }
        return h[end]!=INF;
    }
    P max_flow(int st,int end)
    {
        int maxflow=0,cost=0;
        while(dij(st,end))
        {
            int ff=INF,now=end;
            vector<int> r;
            while(now!=st)
            {
                r.emplace_back(prev[now]);
                ff=min(ff,get<1>(e[prev[now]]));
                now=get<0>(e[prev[now]^1]);
            }
            for(int i:r)
            {
                get<1>(e[i]) -= ff;
                get<1>(e[i^1]) += ff;
            }
            maxflow+=ff;
            cost+=ff*h[end];
        }
        return P(maxflow,cost);
    }
};
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int n,m,st,end;
    cin>>n>>m>>st>>end;
    MCMF solve(n);
    for(int i=1;i<=m;i++)
    {
        int u,v,w,c;
        cin>>u>>v>>w>>c;
        solve.add_edge(u,v,w,c);
    }
    auto [ans1,ans2]=solve.max_flow(st,end);
    cout<<ans1<<" "<<ans2<<endl;
    return 0;
}

有负边的费用流

/*
 author:wuzx
 */

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<utility>
#include<string>
#include<queue>
#include<map>
#include<set>
#include<iterator>
#include<iomanip>
#include<stack>
#include<cstdio>
#define ll long long
#define int long long
#define endl "\n"
#define P pair<int,int>
#define f first
#define s second
using namespace std;
typedef unsigned long long ull;
const int maxn=110;
const int inf=0x3f3f3f3f;
const int mod=998244353;
struct MCMF{
    const int INF,nn;
    struct Node{
        int v,e;
        // Node(int v1,int e1):v(v1),e(e1){}
    };
    vector<tuple<int,int,int> > e;
    vector<vector<int> > g;
    vector<int> h,dis;
    vector<Node> pre;
    MCMF(int n1):nn(n1),INF(inf),g(n1+1),h(n1+1),dis(n1+1),pre(n1+1){}
    void add_edge(int u,int v,int w,int cost)
    {
        if(u==v)
            return;
        g[u].emplace_back(e.size());
        e.emplace_back(v,w,cost);
        g[v].emplace_back(e.size());
        e.emplace_back(u,0,-cost);
    }
    bool dij(int st,int end)//mlogm 正边权
    {
        dis.assign(nn+1,INF);
        vector<int> vis(nn+1,0);
        priority_queue<P,vector<P>,greater<P> >q;
        dis[st]=0;
        q.emplace(0,st);
        while(!q.empty())
        {
            int u=q.top().s;
            q.pop();
            if(vis[u])
                continue;
            vis[u]=1;
            for(int i:g[u])
            {
                auto [v,w,c]=e[i];
                c+=h[u]-h[v];
                if(w&&dis[v]>dis[u]+c)
                {
                    dis[v]=dis[u]+c;
                    pre[v].v=u;
                    pre[v].e=i;
                    if(!vis[v])
                        q.emplace(dis[v],v);
                }
            }
        }
        return dis[end]!=INF;
    }
    void spfa(int st)
    {
        queue<int> q;
        vector<int> vis(nn+1,0);
        fill(h.begin(),h.end(),inf);
        h[st]=0;vis[st]=1;
        q.push(st);
        while(!q.empty())
        {
            int u=q.front();
            q.pop();
            vis[u]=0;
            for(int i:g[u])
            {
                auto [v,w,c]=e[i];
                if(w&&h[v]>h[u]+c)
                {
                    h[v]=h[u]+c;
                    if(!vis[v])
                    {
                        vis[v]=1;
                        q.push(v);
                    }
                }
            }
        }
    }
    P max_flow(int st,int end)
    {
        spfa(st);
        int maxflow=0,cost=0;
        while(dij(st,end))
        {
            int minf=INF;
            for(int i=1;i<=nn;i++)
                h[i]+=dis[i];
            for(int i=end;i!=st;i=pre[i].v)
                minf=min(minf,get<1>(e[pre[i].e]));
            for(int i=end;i!=st;i=pre[i].v)
            {
                get<1>(e[pre[i].e]) -= minf;
                get<1>(e[pre[i].e^1]) += minf;
            }
            maxflow+=minf;
            cost+=minf*h[end];
        }
        return P(maxflow,cost);
    }
};
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int n,m,st,end;
    cin>>n>>m>>st>>end;
    MCMF solve(n);
    for(int i=1;i<=m;i++)
    {
        int u,v,w,c;
        cin>>u>>v>>w>>c;
        solve.add_edge(u,v,w,c);
    }
    auto [ans1,ans2]=solve.max_flow(st,end);
    cout<<ans1<<" "<<ans2<<endl;
    return 0;
}

上下界

无源汇上下界可行流

在无源点和汇点的上下界可行流问题中，我们可以将改问题转化为最大流问题，首先我们假设每条边的下界流都跑满，对每一条边 $(u,v)$ 建立一条上界-下界容量的边，再新建一个源点S，由S向v连一条容量为下界的边，再新建一个汇点T，由u到T连一条容量为下界的边。

建完边之后，对源点和汇点跑一遍最大流，如果S-T满流，则原网络存在可行流。

/*
 author:wuzx
 */
 
#include<bits/stdc++.h>
#define ll long long
#define int long long
#define endl "\n"
#define P pair<int,int>
#define f first
#define s second
using namespace std;
typedef unsigned long long ull;
const int maxn=200010;
const int inf=0x3f3f3f3f;
const int mod=998244353;
int t;
int n,m,k;
struct dinic{
    const int nn;
    int INF = inf;
    struct Edge{
        int to,cap,flow;
        Edge(int to,int cap,int flow):to(to),cap(cap),flow(flow){}
    };
    vector<int> dis,cur;
    vector<Edge> e;
    vector<vector<int>> g;
    dinic(int n1):nn(n1),dis(n1+1),cur(n1+1),g(n1+1){}
    void add(int u,int v,int w)
    {
        g[u].emplace_back(e.size());
        e.emplace_back(v,w,0);
        g[v].emplace_back(e.size());
        e.emplace_back(u,0,0);
    }
    bool bfs(int st,int end)
    {
        fill(dis.begin(),dis.end(),-1);
        dis[st]=0;
        queue<int> q;
        q.push(st);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            for(int i:g[u])
            {
                auto [v,w,fo]=e[i];
                if(dis[v]==-1&&w>0)
                {
                    q.push(v);
                    dis[v]=dis[u]+1;
                }
            }
        }
        return dis[end]!=-1;//若不可以到终点（起点）就返回false 
    }
    int dfs(int st,int end,int flo)//dfs就是求节点u在残量为flo时的最大增量
    {
        if(st==end)
            return flo;
        int delta=flo;
        for(int i=cur[st];i<g[st].size();i++)
        {
            int j=g[st][i];
            auto [v,w,fo]=e[j];
            cur[st]=i;
            if((dis[v]==dis[st]+1)&&w>0)
            {
                int d=dfs(v,end,min(delta,w));
                e[j].cap-=d;
                e[j^1].cap+=d;
                e[j].flow+=d;
                e[j^1].flow-=d;
                delta-=d;
                if(delta==0)
                    break;
            }
        }
        return flo-delta;
    }
    int max_flow(int st,int end)
    {
        int maxflow=0;
        while(bfs(st,end))
        {
            fill(cur.begin(),cur.end(),0);
            maxflow+=dfs(st,end,INF);
        }
        return maxflow;
    }
};
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;
    dinic solve(n+2);
    vector<int> low(m,0),sum(n+1,0);
    for(int i=0;i<m;i++)
    {
        int u,v,up;
        cin>>u>>v>>low[i]>>up;
        solve.add(u,v,up-low[i]);
        sum[u]-=low[i];
        sum[v]+=low[i];
    }
    int tot=0;
    for(int i=1;i<=n;i++)
    {
        if(sum[i]<0)
            solve.add(i,n+2,-sum[i]);
        else
        {
            solve.add(n+1,i,sum[i]);
            tot+=sum[i];
        }
    }
    int flow=solve.max_flow(n+1,n+2);
    if(flow!=tot)
        cout<<"NO"<<endl;
    else
    {
        cout<<"YES"<<endl;
        for(int i=0,j=0;i<m*2;i+=2,j++)
        cout<<solve.e[i].flow+low[j]<<endl;
    }
    return 0;
}

有源汇上下界可行流

我们可以加入一条 T 到 S 的上界为 ∞ ，下界为 0 的边转化为无源汇上下界可行流问题。

若有解，则 S 到 T 的可行流流量等于 T 到 S 的附加边的流量。

有源汇上下界最大流

我们找到网络上的任意一个可行流。如果找不到解就可以直接结束。

否则我们考虑删去所有附加边之后的残量网络并且在网络上进行调整。

我们在残量网络上再跑一次 S 到 T 的最大流，将可行流流量和最大流流量相加即为答案。

/*
 author:wuzx
 */
 
#include<bits/stdc++.h>
#define ll long long
#define int long long
#define endl "\n"
#define P pair<int,int>
#define f first
#define s second
using namespace std;
typedef unsigned long long ull;
const int maxn=200010;
const int inf=0x3f3f3f3f;
const int mod=998244353;
int t;
int n,m,k;
struct dinic{
    const int nn;
    int INF = inf*inf;
    struct Edge{
        int to,cap,flow;
        Edge(int to,int cap,int flow):to(to),cap(cap),flow(flow){}
    };
    vector<int> dis,cur;
    vector<Edge> e;
    vector<vector<int>> g;
    dinic(int n1):nn(n1),dis(n1+1),cur(n1+1),g(n1+1){}
    void add(int u,int v,int w)
    {
        g[u].emplace_back(e.size());
        e.emplace_back(v,w,0);
        g[v].emplace_back(e.size());
        e.emplace_back(u,0,0);
    }
    void add1(int u,int v,int w)
    {
        g[u].emplace_back(e.size());
        e.emplace_back(v,w,0);
    }
    bool bfs(int st,int end)
    {
        fill(dis.begin(),dis.end(),-1);
        dis[st]=0;
        queue<int> q;
        q.push(st);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            for(int i:g[u])
            {
                auto [v,w,fo]=e[i];
                if(dis[v]==-1&&w>0)
                {
                    q.push(v);
                    dis[v]=dis[u]+1;
                }
            }
        }
        return dis[end]!=-1;//若不可以到终点（起点）就返回false 
    }
    int dfs(int st,int end,int flo)//dfs就是求节点u在残量为flo时的最大增量
    {
        if(st==end)
            return flo;
        int delta=flo;
        for(int i=cur[st];i<(int)g[st].size();i++)
        {
            int j=g[st][i];
            auto [v,w,fo]=e[j];
            cur[st]++;
            if((dis[v]==dis[st]+1)&&w>0)
            {
                int d=dfs(v,end,min(delta,w));
                e[j].cap-=d;
                e[j^1].cap+=d;
                e[j].flow+=d;
                e[j^1].flow-=d;
                delta-=d;
                if(delta==0)
                    break;
            }
        }
        return flo-delta;
    }
    int max_flow(int st,int end)
    {
        int maxflow=0;
        while(bfs(st,end))
        {
            fill(cur.begin(),cur.end(),0);
            maxflow+=dfs(st,end,INF);
        }
        return maxflow;
    }
};
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int st,end;
    cin>>n>>m>>st>>end;
    dinic solve(n+2);
    vector<int> low(m),sum(n+1,0);
    for(int i=0;i<m;i++)
    {
        int u,v,up;
        cin>>u>>v>>low[i]>>up;
        solve.add(u,v,up-low[i]);
        sum[u]-=low[i];
        sum[v]+=low[i];
    }
    int tot=0;
    for(int i=1;i<=n;i++)
    {
        if(sum[i]<0)
            solve.add(i,n+2,-sum[i]);
        else
        {
            solve.add(n+1,i,sum[i]);
            tot+=sum[i];
        }
    }
    solve.add(end,st,inf*inf);
    int flow=solve.max_flow(n+1,n+2);
    if(flow!=tot)
        cout<<"please go home to sleep"<<endl;
    else
        cout<<solve.max_flow(st,end)<<endl;
    return 0;
}

有源汇上下界最小流

我们找到网络上的任意一个可行流。如果找不到解就可以直接结束。

否则我们考虑删去所有附加边之后的残量网络。

我们在残量网络上再跑一次 T 到 S 的最大流，将可行流流量减去最大流流量即为答案。

/*
 author:wuzx
 */
 
#include<bits/stdc++.h>
#define ll long long
#define int long long
#define endl "\n"
#define P pair<int,int>
#define f first
#define s second
using namespace std;
typedef unsigned long long ull;
const int maxn=200010;
const int inf=0x3f3f3f3f;
const int mod=998244353;
int t;
int n,m,k;
struct dinic{
    const int nn;
    int INF = inf;
    struct Edge{
        int to,cap,flow;
        Edge(int to,int cap,int flow):to(to),cap(cap),flow(flow){}
    };
    vector<int> dis,cur;
    vector<Edge> e;
    vector<vector<int>> g;
    dinic(int n1):nn(n1),dis(n1+1),cur(n1+1),g(n1+1){}
    void add(int u,int v,int w)
    {
        g[u].emplace_back(e.size());
        e.emplace_back(v,w,0);
        g[v].emplace_back(e.size());
        e.emplace_back(u,0,0);
    }
    void add1(int u,int v,int w)
    {
        g[u].emplace_back(e.size());
        e.emplace_back(v,w,0);
    }
    bool bfs(int st,int end)
    {
        fill(dis.begin(),dis.end(),-1);
        dis[st]=0;
        queue<int> q;
        q.push(st);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            for(int i:g[u])
            {
                auto [v,w,fo]=e[i];
                if(dis[v]==-1&&w>0)
                {
                    q.push(v);
                    dis[v]=dis[u]+1;
                }
            }
        }
        return dis[end]!=-1;//若不可以到终点（起点）就返回false 
    }
    int dfs(int st,int end,int flo)//dfs就是求节点u在残量为flo时的最大增量
    {
        if(st==end)
            return flo;
        int delta=flo;
        for(int i=cur[st];i<(int)g[st].size();i++)
        {
            int j=g[st][i];
            auto [v,w,fo]=e[j];
            cur[st]=i;
            if((dis[v]==dis[st]+1)&&w>0)
            {
                int d=dfs(v,end,min(delta,w));
                e[j].cap-=d;
                e[j^1].cap+=d;
                e[j].flow+=d;
                e[j^1].flow-=d;
                delta-=d;
                if(delta==0)
                    break;
            }
        }
        return flo-delta;
    }
    int max_flow(int st,int end)
    {
        int maxflow=0;
        while(bfs(st,end))
        {
            fill(cur.begin(),cur.end(),0);
            maxflow+=dfs(st,end,INF);
        }
        return maxflow;
    }
};
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int n,m,st,end;
    cin>>n>>m>>st>>end;
    dinic solve(n+2);
    vector<int> sum(n+1,0);
    for(int i=0;i<m;i++)
    {
        int u,v,low,up;
        cin>>u>>v>>low>>up;
        solve.add(u,v,up-low);
        sum[u]-=low;
        sum[v]+=low;
    }
    int tot=0;
    for(int i=1;i<=n;i++)
    {
        if(sum[i]<0)
            solve.add(i,n+2,-sum[i]);
        else if(sum[i]>0)
        {
            solve.add(n+1,i,sum[i]);
            tot+=sum[i];
        }
    }
    solve.add(end,st,inf);
    int flow=solve.max_flow(n+1,n+2);
    if(flow!=tot)
        cout<<"please go home to sleep"<<endl;
    else
    {
        int id=solve.e.size()-1;
        int ans=solve.e[id].cap;
        solve.e[id^1].cap=solve.e[id^1].cap=0;
        cout<<ans-solve.max_flow(end,st)<<endl;
    }
    return 0;
}