最小二乘法的几种拟合函数

目录

1.最小二乘法的原理和解决的问题

2.最小二乘法的公式解法

2.1  拟合h(x) = a * x

2.2 拟合 h(x) = a0 + a1*x

2.3拟合 h(x) = a0 + a1 *x + a3 * x^3

---

 因为采用矩阵法来进行最小二乘法的函数拟合时，会出现系数矩阵的逆矩阵不存在的情况有一定的局限性，所以本篇对公式法进行简单说明。并用c++进行代码的书写。

1.最小二乘法的原理和解决的问题

最下二乘法的形式：

目标函数 =   （观测值  -  理论值）^2

        观测值就是我们实际数据中的值，理论值就是我们进行函数拟合后用拟合函数计算出的值。

本篇中我们以最简单的线性回归为例进行说明。

        我们有n组样本（Xi，Yi） i = （1，2，3，……，n)

        拟合函数的形式：h(x) = a0 + a1 * x + a2 *x^2 + a3 *x^3.

        最小二乘法要做的就是找到最小的一组 a(a0 、a1、a2、a3……），使得

         （h(x) -  yi）^2最小。方法就是对各个系数求偏导，并让偏导数等于0即可。

2.最小二乘法的公式解法

2.1  拟合h(x) = a * x

      对a求偏导得：

 2 *  = 0

 化简得：a = Lxy / Lxx

 其中  Lxx =   ，   Lxy = ，ex为x的均值，ey为y的均值

代码如下：

double calculate(std::vector<double> xs,std::vector<double> ys){

    int len = xs.size();

    double Lxy = 0;
    double Lxx = 0;

    for(int i = 0; i < len ; i++){
        Lxy += xs[i] * ys[i];
        Lxx += qPow(xs[i],2);
    }

    double ret = 0;
    ret = Lxy / Lxx;
    return ret;
}

2.2 拟合 h(x) = a0 + a1*x

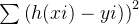对a0和a1分别求偏导的得：

a0： = 0

a1:   2 * = 0

 联立两个方程解得：a0 = ey - a1 * ex 

                                 a1 = Lxy / Lxx（ex、ey、Lxy 和Lxx的含义同上）

代码如下：

double *calculate1(std::vector<double> xs,std::vector<double> ys){
    int len = xs.size();

    //结果
    double *ret = new double[2];

    double ex = 0;//x坐标的均值
    double ey = 0;//y坐标的均值
    double Lxx = 0;//x坐标的平方差*len
    double Lxy = 0;//(Xi-ex)*(Yi-ey)

    //辅助计算
    double xsum = 0;//x的和
    double ysum = 0;//y的和

    //计算xusm
    for(int i = 0; i < len ; i++){
        xsum += xs[i];
        ysum += ys[i];
    }
    ex = xsum / len;
    ey = double(ysum / len);
    for(int i = 0; i < len ; i++){
        Lxx += pow(xs[i]-ex,2);
        Lxy += (xs[i]-ex)*(ys[i]-ey);
    }


    ret[1] = Lxy / Lxx;//计算a1
    ret[0] = ey - ret[1]*ex;//计算a0
    return ret;
}

2.3拟合 h(x) = a0 + a1 *x + a3 * x^3

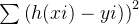对a0、a1和a3分别求偏导的得：

a0:    2* = 0;

a1:   2* = 0;

a3 :   2* = 0

联立方程组解得：

a0 = ey - a1*ex - a3 * ex^3( ey为y 的均值，ex 为x的均值，ex^3为x^3的均值）

a1 = (Lxy * L(x^3)(x^3) - Lx^3 y * Lxy) / (Lxx *L(x^3)(x^3) - Lxy*Lyx)

a3 = (Lx^3y * Lxx - Lxy * L(x^3)*x) / (Lxx*L(x^3*x^3) - Lxy*Lyx)

Lxy、Lxx含义同上

L(x^3)(x^3)表示：

Lx3y表示：

 代码如下：

double *calculate(std::vector<double> xs,std::vector<double> ys){

    int len = xs.size();

    double ey = 0;//y的均值
    double ex1 = 0;//x的均值
    double ex3 = 0;//x的三次方的均值
    double L11 = 0;//x的平方差
    double L12 = 0;//x的3次方的平方差*len
    double L21= 0;//等于L12
    double L1y = 0;//(Xi-ex)*(Yi-ey)的和
    double L2y = 0;//(Xi^3-ex3)*(Yi-ey)的和
    double L22 = 0;//x的3次方的平方差*len
    double Lyy = 0;//y的平方差*len

    double ysum = 0;
    double xsum1 = 0;
    double xsum3 = 0;

    //计算均值
    for(int i = 0; i < len; i++){

        ysum += ys[i];//y的总和

        xsum1 += xs[i];//x的总和
        xsum3 += std::pow(xs[i],3);//x的3次方的总和
    }
    //计算各个值
    ey = ysum / len;
    ex1 = xsum1 / len;
    ex3 = xsum3 / len;

    for(int i = 0 ; i < len ;i++){
        L11 += qPow(xs[i]-ex1,2);//x的方差*len

        L12 += (xs[i]-ex1)*(qPow(xs[i],3)-ex3);

        L1y += (xs[i]-ex1)*(ys[i]-ey);
        L2y += (qPow(xs[i],3)-ex3)*(ys[i]-ey);

        L22 += qPow((qPow(xs[i],3)-ex3),2);//x的3次方的方差*len

        Lyy += qPow(ys[i]-ey,2);
    }
    L21 = L12;
    double ret[3];
    ret[2] = (L2y * L11 - L1y * L21)/(L11 * L22 - L12 * L21);
    ret[1] = (L1y * L22 - L2y * L12)/(L11 * L22 - L12 * L21);
    ret[0] = ey - ret[1]*ex1 - ret[2]*ex3;
   
    return ret;
}

以上是我在编写一个插值函数时遇到矩阵法不可以求出拟合函数后，从原始的概念入手进行的函数拟合，如有差错之处欢迎批评指正。