task03笔记2

· 交互效应模型——定性与定量变量的交互效应

· Example8. 在example.6的模型中，female组与male组的回归函数是两条平行的直线，即它们的斜率——教育程度$educ$对薪资$wage$的偏效应是恒定的，这意味着性别不会对教育的边际回报产生影响。而如果我们想在模型体现或验证两者会相互影响，则可以在原模型中加入交互项$female\ast educ$
$$\text{ wage }={\beta }_0+{\delta }_0\text{ female }+{\beta }_1\text{ educ }+{\delta }_1\text{ female }\ast \text{ educ }+u$$
$$E(\text{ wage|male },educ)={\beta }_0+{\beta }_{1}educ$$
$$E(\text{ wage|female },educ)={\beta }_0+{\delta }_0+\left({\beta }_1+{\delta }_1\right)educ$$

对于这个模型，我们可以做两种假设检验：

1、检验男性与女性的边际教育回报是否相同。这等价于检验假设
$$H_0:{\delta }_1=0\leftrightarrow H_1:{\delta }_1\ne 0$$
2、检验男性与女性的平均工资是否存在性别差异。这等价于检验假设
$$H_0:{\delta }_0={\delta }_1=0\leftrightarrow H_1:\exists {\delta }_j\ne 0,j=0,1$$
显然，对于第一个问题，我们可以使用t检验；对于第二个问题，我们可以使用F检验

直接根据报告表做t检验

wage1_lm3=sm.formula.ols('lwage~female+educ+I(female*educ)+exper+I(exper**2)+tenure+I(tenure**2)',data=wage1).fit()
print(wage1_lm3.summary())
# 使用anova函数做F检验
wage1_lm3_r=sm.formula.ols('lwage~educ+exper+I(exper**2)+tenure+I(tenure**2)',data=wage1).fit()
anova_lm(wage1_lm3_r,wage1_lm3)
t检验结果表明，两性之间教育边际回报相等的假设是不能被拒绝，即两性边际回报可以认为是相等的；但是F检验结果是非常显著的，即两性存在薪资差异。这可能能说明引起两性收入不平等的原因并非来自教育程度。

多分类变量

多分类变量相比于二分类变量也更难处理，我们不能用一个变量的多个取值来定义多分类虚拟变量。如，我们不可以定义季节变量$season$的取值1/2/3/4为春/夏/秋/冬，因为这意味着不同分类之间的差异完全取决于取值之间的差！

正确做法是，用多个二值虚拟变量来表示多分类定性变量。具体的，如果一个变量有n个类别，则需要定义n-1个虚拟变量表示它。以季节变量为例，我们定义三个虚拟变量：spring/summer/fall，当它们其中之一等于1时，代表季节为它们本身；而如果它们全都为0，则代表季节为winter。

· 虚拟变量陷阱——完全共线性

之所以需要这样定义多分类定性变量，是因为如果我们如果将winter也纳入模型中时，这四个变量会满足一个恒等关系式
$$spring+summer+fall+winter=1$$
这说明这四个自变量存在完全共线性，违背了CLM假设中的MLR.4，使得模型完全失效。

1. 如何将一个多分类变量“分解”为多个0-1虚拟变量
2. 分解成多个虚拟0-1变量后，如何用这些变量进行回归而不踩雷。

· Example9. 我们对某大公司的计算机专业人员进行薪水调查，调查的目的是识别和量化哪些影响薪水差异的因素，数据中的变量描述如下：

S：年薪，单位是美元；


X：工作经验，单位是年；


E：教育，1表示高中毕业，2表示获得学士学位，3表示更高学位；


M：1表示为管理人员，0表示非管理人员；

我们以S为因变量，以X/E/M为自变量进行多元回归。其中：X为定量变量，M为二分类变量（且已经0-1化），它们已经可以直接进行回归处理了。但是E则需要进行0-1处理。

现在我们对E进行虚拟变量编码，这也叫One-hot编码。我们使用pandas包的get_dummies函数进行重编码。

在对E进行重编码前，我们先花一点时间介绍一下get_dummies这一函数，让大家明白这个函数的工作原理。该函数会自动变换所有具有对象类型（如字符串）的列，但是如果某列的变量是数值型变量（哪怕它实际上是分类变量），它将不会为该列创建虚拟变量，除非我们将该列的数据类型从数值转化为字符串。

# 使用get_dummies函数
display(pd.get_dummies(demo_df))
print(type(demo_df.Interger_Feature[0]))
demo_df['Interger_Feature']=demo_df['Interger_Feature'].astype(str)

pd.get_dummies(demo_df,columns=['Interger_Feature']) # 指定columns参数，就可以对我们想要虚拟变量化的列进行精准转换
#重编码
data['E']=data['E'].astype(str)
data_dummies=pd.get_dummies(data,columns=['E'])
data_dummies.head()

我们已经将变量E转化为了三个虚拟变量，现在可以进行回归了。注意：不可以直接将三个虚拟变量同时纳入回归当中，我们可以选取一个虚拟变量作为“基组”，然后将其他非基组的虚拟变量纳入回归。这里我们选取高中教育水平$E=1$作为基组，则方程可以这样构建
$$S={\beta }_0+{\beta }_{1}X+{\gamma }_2{E}_2+{\gamma }_3{E}_3+{\delta }_{1}M+u$$

data_lm=sm.formula.ols('S~X+E_2+E_3+M',data=data_dummies).fit()
print(data_lm.summary())

带有自变量函数的回归分析

所谓自变量函数，其实就是将原自变量进行一种变换。变换后的变量一方面可能使模型对数据的拟合效果更佳；另一方面也可以满足一些我们实际的数据分析需求。在这一章节，我们简单介绍三种常见的自变量函数：对数化、二次项化、交互项化。

对数化

我们考虑一般地模型
$$\log (y)={\beta }_0+{\beta }_1\log \left(x_1\right)+{\beta }_2{x}_2+u$$
对于因变量与自变量同为对数的系数，其满足如下公式
$${\beta }_1\approx \frac{\Delta y/y}{\Delta x_1/x_1}\Rightarrow \frac{\Delta y}{y}\approx {\beta }_1\frac{\Delta x_1}{x_1}$$
约等号两边都以增量比例的形式代表增量，于是我们可以将之解读为：在其他因素不变的条件下，$x_1$每增加1%，$y$会增加${\beta }_1\%$。

而对于因变量与自变量一个为对数一个不为对数的系数，以上述模型${\beta }_2$为例，其满足如下公式
$${\beta }_2\approx \frac{\Delta y/y}{\Delta x_2}\Rightarrow \frac{\Delta y}{y}\approx {\beta }_2\Delta x_2$$
约等号一边为纯增量，一边为增量比例的形式，对于该模型我们可以将之解读为：在其他因素不变的条件下，$x_2$每增加1个单位，$y$会增加${\beta }_2\%$。

严格地说，对数化变量系数的解读并没有上面这么简单，上面的解读方法只是一种近似，但是一般情况下我们不用考虑得那么严格。
它的作用非常明显：

1. 正如上面的例子所示，对数变换可以方便地计算变换百分比，于“价格”型变量而言，百分比解释比绝对值解释更有经济意义。
2. 当因变量为严格取正的变量，它的分布一般存在异方差性或偏态性，这容易违背CLM假设的同方差/正态性假设。而对数变换可以缓和这种情况。

然而，对数变换并不能滥用，因为在一些情况下对数变换会产生极端值。首先，存在负值的变量不可以对数变换；其次，当原变量$y$有部分取值位于[0,1]区间时，$log(y)$的负数值会非常大！而线性模型对极端值是非常敏感的，这会影响模型的效果。

1. 对于大数值大区间变量（价格类变量、人口变量等），可取对数变换，如：工资、薪水、销售额、企业市值、人口数量、雇员数量等。
2. 对于小数值小区间变量（时间类变量等），一般不取对数变换，如：受教育年限、工作年限、年龄等。

# 对数化对正态化的作用
## 以hprice1的price为例
### 未经对数化的直方图
hprice1.hist(column='price',figsize=(8,6))

### 对数化后的直方图
hprice1.hist(column='lprice',figsize=(8,6))

二次项

· Example10. 直觉上看，职场里资历越老的人工资水平就越高，于是我们想知道某公司内员工工资水平与单位工作年限之前的关系。很自然地，我们会把模型简单地假设为
$$wage={\beta }_0+{\beta }_{1}exper+u$$

经验告诉我们，随着工作年限的上升，工资提升会逐渐变缓。也就是说，工作年限对工资水平的影响可能不是线性的，而是有一个“弧度”。如何让模型具备这个“弧度”呢？最简单也是最直观的方法就是，在原模型的基础上加入二次项
$$wage={\beta }_0+{\beta }_{1}exper+{\beta }_{2}expe{r}^2+u$$
假设经过OLS估计后，模型为
$$\widehat{\text{ wage }}=3.73+0.298\text{ exper }-0.006{\text{ exper }}^2$$

总结：如果我们在回归建模前认为某个自变量对因变量的影响不是线性的，可以尝试加入二次项，并观察二次项的显著性。如果显著，就说明两者关系确实为非线性的。

交互项

· Example11. 我们用出勤百分比atndrte，读大学前的GPA、ACT来解释一批学生期末考试标准化的成绩。有人认为对于过去成绩不同的学生，出勤率可能具有不同的影响，于是我们在模型中加入两者的交互项
$$\mathrm{stndfnl}={\beta }_0+{\beta }_1\mathrm{atndrte}+{\beta }_2\mathrm{priGP}A+{\beta }_{3}ACT+{\beta }_{4}priGP{A}^2+{\beta }_{5}AC{T}^2+{\beta }_{6}priGPA\cdot \mathrm{atndrte}+u$$
在这里我们想提醒一下大家，在没有学习交互项、二次项的时候，我们会说自变量$x_i$的系数${\beta }_i$是其对因变量$y$的偏效应，这是因为在全为一次项的模型中，$\frac{\Delta y}{\Delta x_i}$就等于系数${\beta }_i$。而加入了交互项、二次项后，我们对存在交互项、二次项的自变量的系数解释就不会那么简单了。我们更关注问题的本质——$x_i$对因变量$y$的偏效应是多少，对于本例而言，出勤率对成绩的偏效应如下所示
$$\frac{\Delta \text{ stndfnl }}{\Delta atndrte}={\beta }_1+{\beta }_6\text{ priGPA }$$
可见，$priGPA$在不同取值下，出勤率对成绩的影响是不一样的。其实有了这个公式，我们可以计算出$priGPA$在不同取值下，出勤率对成绩偏效应的具体值，这一任务非常简单。但是涉及交互问题的假设检验就相对复杂一点，也非常有趣。通常来说，这类问题假设检验有如下两个

1. 出勤率对成绩的影响是否显著？对于这一问题，假设需要设置成这样
   $$H_0:{\beta }_1={\beta }_6=0\leftrightarrow H_1:H_0\text{不成立}$$
   很明显，我们用F检验即可。

# 构建有约束、无约束模型
attend_lm_ur=sm.formula.ols('stndfnl~atndrte+priGPA+ACT+I(priGPA**2)+I(ACT**2)+I(priGPA*atndrte)',data=attend).fit()
attend_lm_r=sm.formula.ols('stndfnl~priGPA+ACT+I(priGPA**2)+I(ACT**2)',data=attend).fit()

# F检验
display(anova_lm(attend_lm_r,attend_lm_ur))
print('结果显著，可以拒绝原假设')

2. 当$priGPA$为一个具体的值时，出勤率在这个值下对对成绩的影响是否显著？

这个问题非常有趣，要回答这个问题，我们需要对原模型做一些小改变。假设我们想验证$priGPA=2.59$时出勤率的显著性，我们需要将原来的$atndrte$修改为$atndrte-2.59$。模型也将变成
$$\mathrm{stndfnl}={\beta }_0+{\beta }_1\mathrm{atndrte}+{\beta }_2\left(GPA-2.59\right)+{\beta }_{3}ACT+{\beta }_4{\left(priGPA-2.59\right)}^2+{\beta }_{5}AC{T}^2+{\beta }_6\left(priGPA-2.59\right)\cdot \mathrm{atndrte}+u$$
我们根据这个模型求偏导会有
$$\frac{\Delta \text{ stndfnl }}{\Delta atndrte}={\beta }_1+{\beta }_6\text{ (priGPA-2.59) }$$
当$atndrte=2.59$时，偏效应正好就是${\beta }_1$！我们只需要查看这个模型的${\beta }_1$显著性就可以回答这一假设检验问题了。

attend['priGPA2']=attend['priGPA']-2.59
attend_lm2=sm.formula.ols('stndfnl~atndrte+priGPA2+ACT+I(priGPA2**2)+I(ACT**2)+I(priGPA2*atndrte)',data=attend).fit()
print(attend_lm2.summary())
print('结果显著，可以拒绝原假设')

5. CLM假设误差分析

5.1 OLS估计另一种更为常用的求解方法

5.1.1 解法步骤

该部分仅作了解即可。

我们以求回归模型
$$y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k+u$$
中${\beta }_1$为例，大体上可分为两步

· step 1，以$x_1$做因变量，对其他自变量做回归
$$x_1={\alpha }_0+{\alpha }_2{x}_2+\cdots +{\alpha }_k{x}_k+r_1$$
记残差为${\hat{r}}_1={\left({\hat{r}}_{11},{\hat{r}}_{21},\cdots ,{\hat{r}}_{n1}\right)}^{\prime }$

· step 2，$y$对残差${\hat{r}}_1$做过原点（无截距）的回归
$$y=\gamma {\hat{r}}_1+u$$
可以证明，${\beta }_1$的估计就是$\hat{y}$
$$\hat{\gamma }={\hat{\beta }}_1=\frac{{\sum }_{i=1}^n{\hat{r}}_{i1}{y}_i}{{\sum }_{i=1}^n{\hat{r}}_{i1}^2}$$
我们仔细品味一下${\beta }_1$的求解过程，会发现它非常符合我们对回归模型系数的理解——在第一步的自变量回归中，残差${\hat{r}}_1$相当于是在$x_1$中排除了$x_2$,……,$x_n$影响后的剩余部分，因此${\hat{\beta }}_1$相当于在度量排除了其余自变量影响后，$x_1$对$y$的影响。而我们回想一下之前我们对${\beta }_1$的解释有一个重要的前置语：“在其他自变量不变的前提下”，这恰恰就是排除其他变量的影响的含义。

看看这种求解方法的结果和之前的求解方法是否一致。

# 以gpa_lm2的ACT系数为例

# 常规解法的结果
print('常规解法的结果:')
display(c2)
print('-------------------------------------------')

# 新求解法
gpa_lm2_pre=sm.formula.ols('ACT~hsGPA',data=gpa1).fit()
gpa1['resid']=gpa_lm2_pre.resid
gpa_lm2_pre2=sm.formula.ols('colGPA~resid-1',data=gpa1).fit()
print('新解法的效果')
print(gpa_lm2_pre2.params[0])

5.1.2 估计系数的方差构成与多重共线性

在MLR.1~MLR.5下，$\mathrm{Var}\left({\hat{\beta }}_1\right)$可计算为
$$\mathrm{Var}\left({\hat{\beta }}_1\right)=\frac{{\sigma }^2}{{\sum }_{i=1}^n{\hat{r}}_{i1}^2}=\frac{{\sigma }^2}{SS{T}_1\left(1-R_1^2\right)}$$

中，$SS{T}_1={\sum }_{i=1}^n{\left(x_{i1}-{\bar{x}}_1\right)}^2$为$x_1$变量本身的完全平方和，$R_1^2$是$x_1$对其他解释变量所作回归的拟合优度判决系数，${\sigma }^2$则是之前提及的随机误差的方差。至此，回归系数估计方差的构成就结构完毕了，它依赖于三个因素：

· 误差方差${\sigma }^2$，随机误差的方差可以理解为数据集的噪声信息，噪声信息越多，估计的不确定性就越大，方差就越大，这点很顺理成章！但是一般来说，对于给定的数据集，误差方差也是随之确定的，我们一般不会在这个因素上下文章。

· 自变量$x_1$本身的总变异$SS{T}_1$，自变量总变异越大，表明自变量散步程度越高，估计越牢靠。关于这个指标，我们会发现：对于一个分析任务来说，样本量越大，总变异也就越大，进而估计方差会变小，这告诉我们更多的随机样本有利于提高估计的精度！

· 自变量间的线性关联程度$R_1^2$，$R_1^2$约接近1，$x_1$与其他自变量之间的线性关系就越强烈，估计方差也越大。这种近似的共线性关系被称为多重共线性(multicolinearity)，它不同于完全共线性（事实上$R_1^2=1$时就是完全共线性），这种现象在数据分析中普遍存在，只是程度有所区别。那么如何衡量共线性的严重程度呢？我们一般用方差膨胀因子(VIF,Variance Inflation Factor)来评判
$$VI{F}_{x1}=\frac{1}{1-R_1^2}$$
若$VIR>10$，意味着共线性很严重，需要采取措施降低共线性。
一种方法是使变量之间尽可能的不相关，关于这点我们可以查看变量之间的皮尔逊相关系数
二种方法是减少自变量的个数。一般而言，模型中自变量个数越多，R方会越大。而$R_1^2$正是$x_1$对其他自变量做回归的判决系数，显然，其他自变量越多，$R_1^2$就越大。这个方法告诉我们，模型的自变量绝非越多越好

总结一下降低估计方差，提高估计精度的方法

1. 采取更合理的数据采样方法，降低数据噪声。
2. 增大数据样本量
3. 根据线性相关程度筛选纳入模型的变量，且切忌纳入过多变量。

5.2 模型误设的误差分析——违反MLR.1的后果是什么

5.2.1 如何理解模型误设

在MLR.1中，我们假设自己设置的模型是“正确的”，即对
$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+u$$
的假设上，我们正确地纳入了所有关键的自变量，且没有纳入多余的自变量。而多纳入一个无关的变量，以及少纳入一个关键的变量，都能算是违反MLR.1，我们可以看看误设模型对模型中变量系数的估计会有怎样子的影响。

5.2.2 模型误设的后果

· 遗漏相关变量

假设真模型为
$$y\sim x_1+x_2+\cdots +x_{k-1}+x_k$$
但我们实际拟合的模型却是
$$y\sim x_1+x_2+\cdots +x_{k-1}$$
假设真模型的系数估计记为${\hat{\beta }}_i$，实际模型的系数估计为${\tilde{\beta }}_i$，那么有
$${\tilde{\beta }}_1={\hat{\beta }}_1+{\hat{\beta }}_k{\tilde{\delta }}_1$$
其中，${\tilde{\delta }}_1$是遗漏变量对其余变量的辅助回归$x_k\sim x_1+x_2+\cdots +x_{k-1}$中$x_1$对应的回归系数。我们观察一下${\tilde{\beta }}_1$的无偏性情况
$$E\left({\tilde{\beta }}_1\mid x\right)={\beta }_1+{\beta }_k{\tilde{\delta }}_1$$
发现，原本正确模型假设下的无偏性$E\left({\hat{\beta }}_1\right)={\beta }_1$，因漏设相关变量$x_k$导致多了偏差${\beta }_k{\tilde{\delta }}_1$。

因此，对于遗漏变量$x_k$，除非${\beta }_k=0$（即$x_k$对$y$完全不影响），或者${\tilde{\delta }}_1=0$（遗漏变量$x_k$与待分析自变量$x_1$不相关），否则遗漏变量会对我们实际估计模型的系数估计产生有偏影响，即我们的系数估计不再是平均意义上的准确！

假设真模型为
$$y\sim x_1+x_2+\cdots +x_{k-1}$$
但实际拟合的模型是
$$y\sim x_1+x_2+\cdots +x_{k-1}+x_k$$
且：$x_k$与其余自变量$x_i$存在相关性，但与因变量$y$不存在相关性（即无法对因变量变异做出解释），此时，我们实际拟合的模型相当于是
$$y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_{k-1}{x}_{k-1}+0x_k+u$$
这种过度设定其实并不违反MLR.1-MLR.4中的任意一条，因为就算将这个无关变量纳入模型，最终拟合出来的变量对应系数也会是0。因此，纳入无关变量这种情况对于建立在前四个假设上的OLS无偏性是没有影响的！即依然有
$$E\left(\widetilde{{\beta }_i}\right)={\beta }_i$$
但是只要$x_k$与其它自变量存在共线性，将其纳入会使其他系数的估计方差变大。以$x_1$的系数为例，假设纳入$x_k$前它的方差是
$$\mathrm{Var}\left({\hat{\beta }}_1\right)=\frac{{\sigma }^2}{SS{T}_1\left(1-R_{1,k-1}^2\right)}$$
而纳入$x_k$后它的方差就变成了
$$\mathrm{Var}\left({\tilde{\beta }}_1\right)=\frac{{\sigma }^2}{SS{T}_1\left(1-R_{1,k}^2\right)}$$
由于而多自变量的模型R方总是大于少自变量模型的R方，即
$$R_{1,k-1}^2<R_{1,k}^2$$
于是最终有
$$\mathrm{Var}\left({\hat{\beta }}_1\right)<\mathrm{Var}\left({\tilde{\beta }}_1\right)$$
因此，对于增加一个对解释因变量无益的自变量，一旦这个无益自变量与其它自变量存在共线性，则会增大其他估计系数的估计方差！

我们总结一下以上的内容：

1. 减少模型中的变量，可能会导致模型其他系数的估计有偏，但是会使系数估计的方差减少，即：增大偏差、减小方差
2. 增加模型中的变量，不会导致模型系数估计有偏，但是会使系数估计的方差增大，即：减小偏差、增大方差

而在实际情况中，我们不可能得知一个真正正确的模型，而是在摸索中慢慢找到适合纳入模型的变量。通常来说，有两种考量纳入变量的方法论：

1. 从少数变量开始，一步步向模型纳入我们认为重要的变量，并通过t检验显著性来判断是否纳入该变量；如果我们认为变量存在二次项效应与交互项效应，可以将其纳入模型并通过联合F检验判断其显著性，直到模型的解释度达到一个较高的水平。
2. 从多数变量开始，一步步将不显著的变量剔除出模型。

这两种方法该用哪一种，视具体情况而定。假若数据集的变量非常多，那我倾向于使用第一种方法，一步步将我们认为重要的变量纳入模型；若变量不多，则第二种方法可以考虑。

对于变量的选择，还有一些自动化的方法，如向前逐步选择、向后逐步选择等等。但我个人认为，这些自动的变量选择方法更关注模型的预测能力，而不注重变量本身对模型的意义，它们更适用于机器学习的预测任务我们总结一下以上的内容：

1. 减少模型中的变量，可能会导致模型其他系数的估计有偏，但是会使系数估计的方差减少，即：增大偏差、减小方差
2. 增加模型中的变量，不会导致模型系数估计有偏，但是会使系数估计的方差增大，即：减小偏差、增大方差

而在实际情况中，我们不可能得知一个真正正确的模型，而是在摸索中慢慢找到适合纳入模型的变量。通常来说，有两种考量纳入变量的方法论：

1. 从少数变量开始，一步步向模型纳入我们认为重要的变量，并通过t检验显著性来判断是否纳入该变量；如果我们认为变量存在二次项效应与交互项效应，可以将其纳入模型并通过联合F检验判断其显著性，直到模型的解释度达到一个较高的水平。
2. 从多数变量开始，一步步将不显著的变量剔除出模型。

这两种方法该用哪一种，视具体情况而定。假若数据集的变量非常多，那我倾向于使用第一种方法，一步步将我们认为重要的变量纳入模型；若变量不多，则第二种方法可以考虑。

对于变量的选择，还有一些自动化的方法，如向前逐步选择、向后逐步选择等等。但我个人认为，这些自动的变量选择方法更关注模型的预测能力，而不注重变量本身对模型的意义，它们更适用于机器学习的预测任务，而不适用于回归分析，因为回归分析中最重要的意义就是“解释与推断”。，而不适用于回归分析，因为回归分析中最重要的意义就是“解释与推断”。

5.3 模型不满足正态性的分析——违反MLR.6的后果是什么

如何理解与观测正态性假设

假设假定随机误差$u$在任何自变量$x$已知的条件下服从正态分布
$$u\mid x\sim N\left(0,{\sigma }^2\right)$$
即每个样本的误差$u_1,u_2,...,u_n$都是来源于一个正态总体。然而，随机误差在数据集中是根本观测不到的，而由于在$x$已知的条件下，$u$的正态性等价于$y$的正态性，因此我们只需要查看样本因变量$y$的分布图就可以大致判断正态性了。

然而，因变量$y$不为正态分布的情况是非常常见的，以下面的$narr86$为例，它统计了青年人在某一特定年份被拘捕的次数。很明显，绝大部分青年人都没有被拘捕过，因此该变量的分布是一个严重的偏态分布，不可能为正态分布

# 频数直方图
crime1=pd.read_stata('crime1.dta')
crime1.hist(column='narr86',figsize=(8,6))
print(crime1.narr86.value_counts())

5.3.2 违背正态性假设的后果

，因此违背正态性假设不会影响OLS系数估计的准确性与稳定性。

但是我们在进行假设检验的时候，基于t统计量与F统计量的推断是以满足MLR.6为前提的，这是否意味着对于narr86这种因变量而言，我们无法对其进行t检验与F检验呢？幸运的是，回答是否定的。得益于中心极限定理，我们有下述定理成立

· 定理： 在MLR.1-MLR.5假定下，OLS估计系数的抽样分布满足
$$\frac{{\hat{\beta }}_j-{\beta }_j}{\mathrm{se}\left({\hat{\beta }}_j\right)}\Rightarrow N(0,1)$$
即，OLS的系数估计满足渐进正态性，这意味着在大样本容量下，OLS估计系数是近似正态分布的。

接下来的问题是，大样本下OLS估计是渐进正态分布的，按理来说应当使用标准正态分布作参考而不是用t分布作参考。但从实证角度来说，使用t分布进行大样本假设检验也是合理的，即以下写法是合理的
$$\frac{{\hat{\beta }}_j-{\beta }_j}{\mathrm{se}\left({\hat{\beta }}_j\right)}\Rightarrow t_{n-k-1}$$
这是因为，当t分布自由度df达30以上时，就已经接近为正态分布了，而大样本下样本容量$n$的大数值将让自由度$n-k-1$也达到一个很大的数值，因此使用t分布进行检验实际上是没问题的！

最后的问题是，样本容量究竟要有多大才算是大样本呢？这没有一个固定的答案，部分学者认为大于等于30就可以了，当然样本量越多越好这是毋庸置疑的。

5.4 异方差的分析——违反MLR.5的后果是什么

同方差假设MLR.5：随机误差$u$的条件方差恒为一个常数，即
$$\mathrm{Var}\left(u\mid x_1,\cdots ,x_k\right)={\sigma }^2$$
这个假设还可以拓展成因变量$y$的同方差性
$$\mathrm{Var}\left(y\mid x_1,\cdots ,x_k\right)={\sigma }^2$$

于给定样本的$y_1,y_2,\dots ,y_n$，在每一个自变量$x_j$测度下，它们的方差都应当是恒定的。这句话可以理解成，因变量/随机误差的方差在每一个自变量$x_j$下都不随自变量的变化而变化；而只要其在某一个自变量$x_j$下的方差是不稳定的，则同方差假设就不成立！

Example12
我们研究住房价格price的影响因素，并初步确定模型为
$$\text{ price }={\beta }_0+{\beta }_1\text{ lotsize }+{\beta }_2\text{ sqrft }+{\beta }_{3}bdrms+u$$
即，我们纳入了三个自变量：lotsize,sqrft,bdrms。要想观测样本是否存在异方差性，

• 第一种方法就是直接查看因变量$y$分别在三个自变量下的散点分布图，看看因变量在自变量值变化时的散布特征是否不变。
• .另一种观测异方差的方法是先进行OLS拟合，并以0为参考基准，观测残差在三个自变量上的表现

# 使用数据集hprice1，前面已经加载过
fig=plt.figure(figsize=(13,6))
ax1=fig.add_subplot(1,3,1)
hprice2=hprice1[hprice1['lotsize']<80000] #去掉了一个极端点，方便观察
plt.scatter(hprice2.lotsize,hprice2.price,axes=ax1)
ax1.set_xlabel('lotsize')
ax1.set_ylabel('price')

ax2=fig.add_subplot(1,3,2)
plt.scatter(hprice1.sqrft,hprice1.price,axes=ax2)
ax2.set_xlabel('sqrft')
ax2.set_ylabel('price')

ax3=fig.add_subplot(1,3,3)
plt.scatter(hprice1.bdrms,hprice1.price,axes=ax3)
ax3.set_xlabel('bdrms')
ax3.set_ylabel('price')

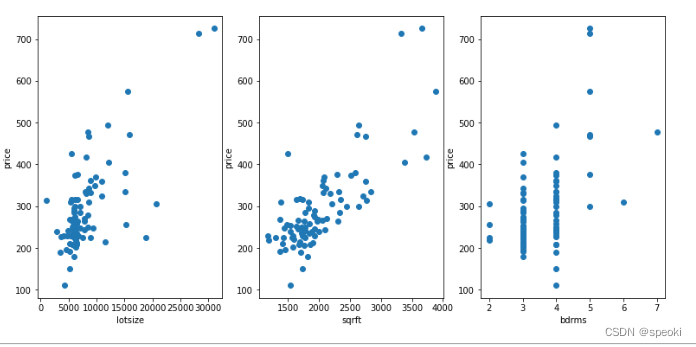
lotsize与sqrft的散布情况相对稳定，异方差的情况并不明显；而bdrms就不一样了，当bdrms=3时，因变量值分布呈现出往较小值偏移的特征，表现为上面稀疏，下面稠密。而bdrms=4时，因变量值的分布则相对对称，这说明price在bdrms上存在异方差的现象

5.4.2 违背同方差假设的后果

1. 模型形式误设（导致违背MLR.1）以及随机误差的非正态性对模型的影响并不明显
2. 违反同方差假设的后果就相对严重了:

• 首先由于MLR.1-MLR.4仍然成立，因此系数估计的无偏性依然成立。
• 异方差下，OLS估计不再是最优线性无偏估计。
• 异方差下，估计系数的方差计算不再准确，从而影响到标准误的计算，进而影响到t检验与F检验的有效性。

6. 异方差下的回归分析

1. OLS不再最优、
2. t检验与F检验不再稳健。
   在这一节我们就要针对这两个问题提出解决的方法。

在这一章节我们将学习：

1. 在异方差下如何重新估计标准差/标准误，并进行稳健的推断（假设检验）
2. 如何用假设检验检测数据的异方差性
3. 如何修正OLS估计方法达到最优（广义OLS法-GLS）

6.1 异方差稳健的t检验与F检验

稳健方法，就是这种方法不论是在异方差还是同方差下都可以进行使用。

6.1.1 重新估计方差

同方差假设下$\widehat{{\beta }_j}$的方差估计：
$$\mathrm{Var}\left({\hat{\beta }}_j\right)=\frac{{\sigma }^2}{{\sum }_{i=j}^n{\hat{r}}_{ij}^2}=\frac{{\sigma }^2}{SS{T}_j\left(j-R_j^2\right)}$$
事实上，这个方差估计有一个更广义的表达
$$\mathrm{Var}\left({\hat{\beta }}_j\right)=\frac{\sum {\hat{r}}_{ij}^2{\sigma }_i^2}{RS{S}_j^2}$$
在同方差假设下，由于${\sigma }_i=\sigma$，才有了上面化简了的表达式。
在异方差下，用残差$\widehat{u_i}$代替，即$\widehat{{\sigma }_i}=\widehat{u_i}$，系数重新估计的方差就变为了
$$\widehat{\mathrm{Var}\left({\hat{\beta }}_j\right)}=\frac{\sum {\hat{r}}_{ij}^2{\hat{u}}_i^2}{RS{S}_j^2}$$
至此，我们就可以利用新的估计方差进行稳健t检验与F检验了。

6.1.2 稳健t检验

对于单参数检验问题，我们使用稳健t检验。

先看单参数检验问题
$$H_0:{\beta }_j={\beta }_{j0}\leftrightarrow H_1:{\beta }_j\ne {\beta }_{j0}$$
定义t统计量
$$t=\frac{{\hat{\beta }}_j-{\beta }_{j0}}{\mathrm{se}\left({\hat{\beta }}_j\right)}\approx N\left(0,1\right)$$
注意，此时t统计量不再服从t分布，而是服从标准正态分布

# 以前面的price1_lm为例
# hprice1_lm=sm.formula.ols('price~lotsize+sqrft+bdrms',data=hprice1).fit()
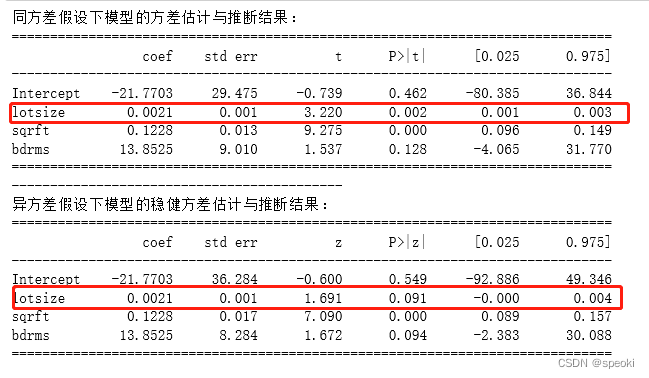
print('同方差假设下模型的方差估计与推断结果：')
print(hprice1_lm.summary().tables[1])
print('-------------------------------------------')
hprice1_lm_1=sm.formula.ols('price~lotsize+sqrft+bdrms',data=hprice1).fit(cov_type='HC0', use_t=False)
# use_t：稳健t检验是否使用t分布进行推断，False表示拒绝使用t分布，改用标准正态分布
print('异方差假设下模型的稳健方差估计与推断结果：')
print(hprice1_lm_1.summary().tables[1])

异方差稳健t检验的结果与普通t检验的结果的不同：
lotsize在普通t检验下是显著的，但在稳健t检验中是不显著的。

6.1.3 稳健F检验

多参数的联合检验，我们使用稳健F检验

稳健F检验的问题设置与原来的F检验一样，且它们的F检验统计量也完全一样，即
$$F=\frac{\left(RS{S}_r-RS{S}_{ur}\right)/q}{RS{S}_{ur}/(n-k-1)}$$
在稳健检验下，F统计量并不严格服从F分布，而是渐进服从自由度为$q$的卡方分布。

我们考虑下述模型
$$cumgpa={\beta }_0+{\beta }_{1}sat+{\beta }_{2}hsperc+{\beta }_{3}tothrs+{\beta }_{4}female+{\beta }_{5}black+{\beta }_{6}white+u$$
并做假设检验
$$H_0:{\beta }_5={\beta }_6=0\leftrightarrow H_1:H_0\text{不成立}$$

#载入数据
gpa3=pd.read_stata('gpa3.dta')
gpa3=gpa3[gpa3['term']==2]
# 直接训练无约束模型，并采用稳健估计训练
gpa3_lm=sm.formula.ols('cumgpa~sat+hsperc+tothrs+female+black+white',data=gpa3).fit(cov_type='HC0')

hypotheses='(black=0),(white=0)' # 另一种做联合检验的形式，直接将原假设写出来
gpa3_lm.wald_test(hypotheses,use_f=True,scalar=False)

6.2 异方差的诊断

关于检验方差是否与自变量无关的方法，最常用的便是BP异方差检验与White异方差检验。

6.2.1 BP异方差检验

· 检验思想

我们取原假设为：假定同方差假设正确，即
$$\mathrm{Var}\left(u\mid x_1,\cdots ,x_k\right)={\sigma }^2$$
由于MLR.2假设：$E\left(u\mid x_1,\cdots ,x_k\right)=0$的成立，则同方差假设等价为
$$E\left(u^2\mid x_1,\cdots ,x_k\right)={\sigma }^2$$

BP检验的实质是检验异方差与所有自变量的一次项无关，这就等价于对一个以$u^2$为因变量，以$x_j$为自变量的线性回归模型
$$u^2={\delta }_0+{\delta }_1{x}_1+{\delta }_2{x}_2+\cdots +{\delta }_k{x}_k+v$$
做全部变量系数的联合显著性检验，于是原假设变为
$${\mathrm{H}}_0:{\delta }_1={\delta }_2=\cdots ={\delta }_k=0$$
如果原假设被拒绝，就意味着存在一种与某自变量一次项相关的异方差。

BP检验的步骤

1. 使用OLS法估计模型
   $$y\sim x_1+x_2+\cdots +x_{k-1}+x_k$$
   获得残差的平方${\hat{u}}^2$

2. 使用OLS估计法估计模型
   $${\hat{u}}^2\sim x_1+x_2+\cdots +x_{k-1}+x_k$$

3. 对所有变量系数做联合检验，可用F检验或大样本LM检验。
   · 用python实现BP检验

from statsmodels.stats.diagnostic import het_breuschpagan
#直接输出
hprice_lm=sm.formula.ols('price~lotsize+sqrft+bdrms',data=hprice1).fit()
hprice_lm_reg=sm.formula.ols('price~lotsize+sqrft+bdrms',data=hprice1)
het_breuschpagan(hrpice1_1m_reg.exog)

# 定义一个输出bp检验的函数
def bp_test(res,X):
	result_bp_test=sm.stats.diagnostic.het_breuschpagan(res,X)
	bp_lm_statistic=result_bp_test[0]
	bp_lm_pval = result_bp_test[1]
    bp_F_statistic= result_bp_test[2]
    bp_F_pval = result_bp_test[3]
    bp_test_output=pd.Series(result_bp_test[0:4],index=['bp_lm_statistic','bp_lm_pval','bp_F_statistic','bp_F_pval'])    
    return bp_test_output

bp_test(hprice1_lm.resid,hprice1_lm_reg.exog)

6.2.2 White异方差检验

BP检验考虑的是是否存在与变量的一次项相关的异方差，而White检验则增加了对所有变量二次项以及交互项的考察。

假若模型包含三个变量，BP检验所检验的模型是
$$y\sim x_1+x_2+x_3$$
而White检验所检验的模型是
$$y\sim x_1+x_2+x_3+{x_1}^2+{x_2}^2+{x_3}^2+x_1{x}_2+x_1{x}_3+x_2{x}_3$$
White检验虽然考虑的问题范围更广，但是由于回归元个数指数级增长，模型自由度相比于BP检验大大降低，对于自变量较多的情况，White检验可能并不如BP检验合适。

from statsmodels.stats.diadnostic import het_white
#White检验函数在python上的使用与BP检验完全一样
def white_test(res,X):
	result_bp_test = sm.stats.diagnostic.het_white(res, X)
    bp_lm_statistic = result_bp_test[0]
    bp_lm_pval = result_bp_test[1]
    bp_F_statistic= result_bp_test[2]
    bp_F_pval = result_bp_test[3]
    white_test_output=pd.Series(result_bp_test[0:4],index=['white_lm_statistic','white_lm_pval','white_F_statistic','white_F_pval'])    
    return white_test_output
    
white_test(hprice1_lm.resid,hprice1_lm_reg.exog)

6.3 广义最小二乘法

——回归存在异方差的另一种解决方法
异方差可以用自变量的函数被表达出来。如果它能被我们找出来，我们就可以是加权最小二乘估计WLS；如果由于函数形式复杂而无法被判断出来，我们则使用可行的广义最小二乘估计FGLS。

6.3.1 加权最小二乘法

加权最小二乘法的原理非常简单。

假设异方差的形式除去一个常数外是已知的，即
$$\mathrm{Var}(u\mid x)={\sigma }^{2}h(x)$$
那么如果我们在原模型两边同除以$\frac{1}{\sqrt{h\left(x\right)}}$，即
$$\frac{y}{\sqrt{h\left(x\right)}}=\frac{{\beta }_0^{\ast }}{\sqrt{h\left(x\right)}}+{\beta }_1^{\ast }\frac{x_1}{\sqrt{h\left(x\right)}}+\cdots +{\beta }_k^{\ast }\frac{x_k}{\sqrt{h\left(x\right)}}+\frac{u}{\sqrt{h\left(x\right)}}$$

并将带有$\frac{1}{\sqrt{h\left(x\right)}}$的自变量与随机误差视作是新的变量与随机误差，则问题就是同方差情形了，我们可以使用OLS估计。

鉴别简单的异方差形式，并用statsmodels包中的wls函数进行wls估计。

· Example13. 我们想研究27家企业主管人数Y与工人人数X的关系。由于只有一个自变量，一开始我们可以考虑简单线性回归模型
$$Y={\beta }_0+{\beta }_{1}X+u$$

##查看散点图 Y.X
fig=plt.sigure(figsize=(13,6))
ax1=fig.add_subplot(1,2,1)
plt.scatter(data.X,data.Y,axes=ax1)
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_title('Y|X')
##查看ols估计的残差与X的散点图
data_lm=sm.formula.ols('Y~X',data=data)
print(bp_test(data_lm.resid,data_lm_reg.exog))
print("*********")
#使用whiite检验
data_lm_reg=sm.formula.ols('Y~X',data=data)
print(white_test(data_lm.resid,data_lm_reg.exog))

bp检验与White检验均表示，回归确实存在明显的异方差线性。且根据散点图，我们可以看到随着X的增大，样本的分布越来越分散，即方差越来越大。我们设想：方差可能与X的二次项成正比（一次项也有可能，言之有理即可），于是我们假定
$$\mathrm{Var}(u\mid x)={\sigma }^2{x}^2$$

data_lm_wls=sm.formula.wls('Y~X',weights=1/data.X**2,data=data).fit()
#注意weights传入的是一个数组，不是一个表达式，如果方差函数为h(x)，则要传入1/h(x)的数组
print(data_lm.summary().tables[1])
print(data_lm_wls.summary().tables[1])

6.3.2 可行的广义最小二乘法

FGLS将$h(x)$假设为
$$h(x)=\exp \left({\delta }_0+{\delta }_1{x}_1+\cdots +{\delta }_k{x}_k\right)$$
则条件方差的表达式就有
$$\mathrm{Var}(u\mid x)=E\left(u^2\mid x\right)={\sigma }^2\exp \left({\delta }_0+{\delta }_1{x}_1+\cdots +{\delta }_k{x}_k\right)$$
进而有
$$E\left(u^2\mid x\right)={\sigma }^2\exp \left({\delta }_0+{\delta }_1{x}_1+\cdots +{\delta }_k{x}_k\right)\Rightarrow \log \left(u^2\right)\sim x_1+\cdots +x_k$$
也就是说，我们先用OLS估计求解一个以$\log \left({\hat{u}}^2\right)$为因变量的线性回归模型，再将该模型进行指数化处理，便可以得到$h(x)$的估计形式了。

我们总结出以下步骤：

1. 做回归$y\sim x_1+\cdots x_k$，得到残差$\hat{u}$
2. 做回归$\log \left({\hat{u}}^2\right)\sim x_1+\cdots +x_k$，得到拟合值$\hat{g}$
3. 计算函数$\hat{h}=\exp (\hat{g})$
4. 以$1/\hat{h}$做权重，用wls估计模型$y\sim x_1+\cdots x_k$

---

statsmod

els.api
statsmodels.api
statsmodels 分为
statsmodels.api横截面模型和方法
statsmodels.tsa.api时间序列模型和方法
statsmodels.formula.api使用公式字符串和dataframe指定模型的便捷接口
回归
类描述OLS(endog[, exog, missing, hasconst])普通最小二乘
WLS(endog, exog[, weights, missing, hasconst])加权最小二乘
GLS(endog, exog[, sigma, missing, hasconst])广义最小二乘
GLS##所谓自变量函数，其实就是将原自变量进行一种变换。变换后的变量一方面可能使模型对数据的拟合效果更佳；另一方面也可以满足一些我们实际的数据分析需求。在这一章节，我们简单介绍三种常见的自变量函数：对数化、二次项化、交互项化。AR(endog[, exog, rho, missing, hasconst])具有 AR 协方差结构的广义最小二乘
RecursiveLS(endog, exog[, constraints])递归最小二乘
RollingOLS(endog, exog[, window, min_nobs, …])滚动普通最小二乘法
RollingWLS(endog, exog[, window, weights, …])滚动加权最小二乘法

插值
类描述BayesGaussMI(data[, mean_prior, cov_prior, …])使用高斯模型的贝叶斯插值。
MI(imp, model[, model_args_fn, …])MI 使用提供的 imputer 对象执行多重插值。
MICE(model_formula, model_class, data[, …])链式方程的多重插值。
MICEData(data[, perturbation_method, k_pmm, …])包装数据集以允许使用 MICE 处理丢失的数据。

离散和计数模型
logit(endog,exog,[,check_rank])Logi模型
probit(endog,exog,[,check_rank])概率模型
MNLogit(endog,exog,[,check_rank])多项logit