蓝桥杯2014年第五届真题——斐波那契（矩阵快速幂）

蓝桥杯2014年第五届真题——斐波那契（矩阵快速幂）

1.题目描述
2.输入输出

3.样例输入输出

4.解题思路
思路一：暴力求解
最常规的思路，一看到斐波那契数列就用递归去写，因此可以写一个斐波那契的函数，然后调用函数来写

#include<bits/stdc++.h>
using namespace std;
int fb(int n){
	if(n==1 || n==2) return 1;
	else return fb(n-1)+fb(n-2);
}
int main(){
	int n,m,p;
	cin>>n>>m>>p;
	long long kount=0;
	for(int i=1;i<=n;i++){
		kount+=fb(i);
	}
	cout<<kount;
	cout<<fb(m);
	cout<<p;
	cout<<(kount%fb(m))%p;
	
	
}

很遗憾，这样做在n非常大的时候会超时。因此如果在蓝桥杯中使用递归暴力去求解这题，只能骗到一部分分数，没办法完全ac掉。

思路二：矩阵快速幂
先了解一下快速幂，所谓快速幂，就是快速的求某一个数的多少次幂，其时间复杂度是O（logn），与朴素的O（n）相比，效率得到了极大的提高，它的基本原理是二进制
快速幂：
对于a^n ， n一定可以用二进制表示。
如156（10）=10011100（2）
求解a^156，原来要进行156-1=155次乘法运算，现在的差不多运算次数就是他 二进制的长度二进制中1的个数=84=24次

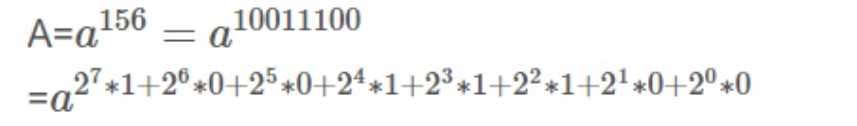
快速幂模板函数

long long fastpow(long long x,long long y)
{
    long long a=1;//a为结果
    while(y)
    {
        if(y&1) a=a*x;
        x=x*x;//一个中间转移量. y每右移一次, x 就多一个平方
        y=y>>1;
    }
    return a;
}

矩阵快速幂：
1.相对于一般的快速幂，矩阵快速幂仅仅是把他的底数和乘数换成了矩阵形式，而相应的乘法运算什么的也遵循矩阵的运算法则。
2.矩阵快速幂的难点主要是在关系矩阵的构造上，只要关系矩阵构造出来了，其他的就只是套模板运算而已。

矩阵

struct node {
    int mat[15][15];//定义矩阵 
}x,y;

矩阵乘法

node mul(node x,node y){//矩阵乘法 
    node tmp;
    for(int i=0;i<len;i++){
        for(int j=0;j<len;j++){
            tmp.mat [i][j]=0;
            for(int k=0;k<len;k++){
                tmp.mat [i][j]+=(x.mat [i][k]*y.mat [k][j])%mod;
            }
            tmp.mat [i][j]=tmp.mat[i][j]%mod;
        }
    }
    return tmp;
}

矩阵快速幂

node matpow(node x,node y,int num){//矩阵快速幂 
    while(num){
        if(num&1){
            y=mul(y,x);
        }
        x=mul(x,x);
        num=num>>1;
    }
    return y;
}

斐波那契数列关系矩阵递推式

本题参考代码（源自网络）

#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;
LL llmul( LL a,LL b,LL mod ) {
    a%=mod;a+=mod;a%=mod;
    b%=mod;b+=mod;b%=mod;
    if ( a<b )    swap( a,b );
    LL ret=0;
    while ( b ) {
        if ( b&1 )ret=( ret+a )%mod;
        a=( a<<1 )%mod;
        b/=2;
    }
    return ret;
}
struct matrix {
    LL x[3][3];
    matrix() {memset( x,0,sizeof x );}
};
matrix mmul( matrix &A,matrix &B,LL mod ) {
    matrix ret;
    for ( int i=1; i<=2; i++ )
        for ( int j=1; j<=2; j++ )
            for ( int k=1; k<=2; k++ )
            ret.x[i][j]=( ret.x[i][j]+llmul( A.x[i][k],B.x[k][j],mod ) )%mod;
    return ret;
}
matrix E,A;
LL fib( LL n,LL mod ) {
    matrix O=E,B=A;
    while ( n ) {
        if ( n&1 )O=mmul( O,B,mod );
        B=mmul( B,B,mod );
        n/=2;
    }
    return O.x[1][2];
}
LL solve( LL n,LL m,LL mod ) {//f(n)%f(m)%mod
    LL t=n/m;
    //(f(m-1)^t*f(n%m))%f(m)%mod;
    //f(i)^2%f(i-1)=(-1)^(i+1)
    LL p=t/2,q=t%2;
    //{f(m-1)^q*(-1)^(pm)*f(n%m)}%f(m)%mod
    LL fuhao=p*m%2==0?1:-1;
    if ( q==0 ) {
        LL ans=fib( n%m,mod )*fuhao;
        ans%=mod;
        ans+=mod;
        return ans%mod;
    }
    if ( n%m==0 )return 0;
    //f(m-1)*f(n%m)*fuhao%f(m)%mod
    //x%y%mod=(x-a*y)%mod
    //a=[x/y]
    LL x=(llmul(fib(n%m,mod),fib(m-1,mod),mod)*fuhao%mod+mod)%mod;
    LL y=fib(m,mod);
    LL a=fib(n%m-1,mod);
    if(n%m%2==0)    a--;
    if(fuhao<0)    a++;
    a=(a%mod+mod)%mod;
    return ((x-llmul(a,y,mod))%mod+mod)%mod;
}
int main ()
{
    A.x[1][2]=A.x[2][1]=A.x[2][2]=1;
    E.x[1][1]=E.x[2][2]=1;
    LL n,m,mod;
    cin>>n>>m>>mod;
    cout<<( solve( n+2,m,mod )-1+mod )%mod<<endl;//S(n)=f(n+2)-1
    return 0;
}