A*算法求解八数码问题实验

最新推荐文章于 2025-03-04 21:11:39 发布

Conn_w

最新推荐文章于 2025-03-04 21:11:39 发布

阅读量2.7k

点赞数 27

文章标签：算法 linux 前端 c++ visual studio windows 人工智能

本文链接：https://blog.csdn.net/m0_52448367/article/details/136144724

版权

A*算法求解八数码问题实验

一、实验目的

熟悉和掌握启发式搜索的定义、估价函数和算法过程，并利用A*算法求解N数码难题，理解求解流程和搜索顺序。

二、实验思路

以8数码问题和15数码问题为例实现A*算法的求解程序（编程语言不限，如Python等），要求设计两种不同的估价函数。

三、实验原理

A算法是一种启发式图搜索算法，其特点在于对估价函数的定义上。对于一般的启发式图搜索，总是选择估价函数f值最小的节点作为扩展节点。因此，f是根据需要找到一条最小代价路径的观点来估算节点的，所以，可考虑每个节点n的估价函数值为两个分量：从起始节点到节点n的实际代价以及从节点n到达目标节点的估价代价。
A算法中，若对所有的x存在h(x)≤h*(x),则称h(x)为的下限，表示某种偏于保守的估计。采用的下限h(x)为启发函数的A算法，称为A算法，其中限制：h(x)≤h(x)十分重要，它能保证A算法找到最优解。在本问题中，g(x)相对容易得到，就是从初始节点到当前节点的路径代价，即当前节点在搜索树中的深度。关键在于启发函数h(x)的选择，A算法的搜索效率很大程度上取决于估价函数h(x)。一般而言，满足h(x)≤h*(x)前提下，h(x)的值越大越好，说明其携带的启发性信息越多，A算法搜索时扩展的节点就越少，搜索效率就越高。
传统的BFS是选取当前节点在搜索树中的深度作为g(x)，但没有使用启发函数h(x)，在找到目标状态之前盲目搜索，生成了过多的节点，因此搜索效率相对较低。
本实验分别使用不在位的元素个数和曼哈顿距离作为启发函数h(x)。每次从open表中选取时，优先选取估价函数最小的状态来扩展。
A算法的估价函数可表示为：f’(n) = g’(n) + h’(n)
这里，f’(n)是估价函数，g’(n)是起点到终点的最短路径值（也称为最小耗费或最小代价），h’(n)是n到目标的最短路经的启发值。由于这个f’(n)其实是无法预先知道的，所以实际上使用的是下面的估价函数：f(n) = g(n) + h(n)
其中g(n)是从初始结点到节点n的实际代价，h(n)是从结点n到目标结点的最佳路径的估计代价。在这里主要是h(n)体现了搜索的启发信息，因为g(n)是已知的。用f(n)作为f’(n)的近似，也就是用g(n)代替g’(n)，h(n)代替h’(n)。这样必须满足两个条件：
(1) g(n)>=g’(n)（大多数情况下都是满足的，可以不用考虑），且f必须保持单调递增。
(2) h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h’(n);第二点特别的重要。可以证明应用这样的估价函数是可以找到最短路径的。
具体步骤：从初始状态S_0出发，分别采用不同的操作符作用于生成新的状态x并将其加入open表中（对应到状态空间图中便是根节点生成新的子节点n） ,接着从open表中按照某种限制或策略选择一个状态x使操作符作用于x又生成了新的状态并加入open表中(状态空间图中相应也产生了新的子节点)，如此不断重复直到生成目标状态。
对于以上所述的“某种策略”，在图搜索过程中，若该策略是依据进行排序并选取最小的估价值，则称该过程为A*算法。

四、实验结果

表1 不同启发函数h(n)求解8数码问题的结果比较
在这里插入图片描述

五、实验过程

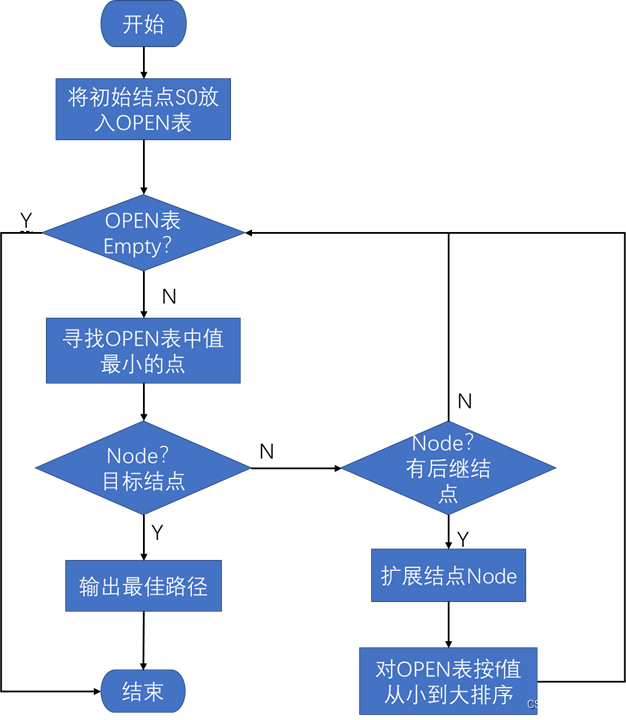
1、画出A算法求解N数码问题的流程图
根据A算法的实验原理，f=g(n) +h(n) ；这样估价函数f(n)在g(n)一定的情况下，会或多或少的受距离估计值h(n)的制约，节点距目标点近，h值小，f值相对就小，能保证最短路的搜索向终点的方向进行, 因此f是根据需要找到一条最小代价路径的观点来估算节点的。设计A算法的流程图如图1所示，按照流程图编写伪代码，进而编写完整的程序。其中OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。在扩展结点时，还需要考虑两个表即OPEN表和CLOSED表中是否存在了该节点的后继节点。

2、分析不同的估价函数对A算法性能的影响
对于同一问题启发函数h(n)可以有多种设计方法。在本次时实验中，通过选用“将牌不在位数”和“将牌‘不在位’的距离和”两种不同的启发函数，同时还编写了不考虑h值进行搜索，即不采用启发性搜索的算法（按照广度优先搜索的策略）。正如表1所示，我们通过将第一种和第二种启发函数对比，发现第二种启发函数优于第一种启发函数，将采用启发函数与不采用启发性函数对比发现，采用启发性函数远远优于不采用启发性函数。
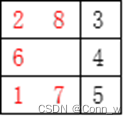
下面，以图4.2.2为例，分析第二种启发函数求解的过程。第二种启发函数为h(n)=将牌‘不在位’的距离和，初始时的值为6,将牌1：2，将牌2：1，将牌6：2，将牌7：1，将牌8:2。在实验结果演示（表1）时，并没有选取初始状态来比较不同启发函数以及不采用启发函数对求解效率的影响，而是选取了图2初始状态进行演示，因为图3的步骤较为复杂，对于不同启发函数对于实验结果和实验效率的影响较为明显。第三种启发函数是按照广度优先搜索的策略。
在这里插入图片描述

3、根据宽度优先搜索算法和A算法求解八数码问题的结果，分析启发式搜索的特点
根据表1的结果，我们可以发现采用A算法求解八数码问题时间以及搜索的节点数目远远小于采用宽度优先搜索算法，这说明对于八数码问题，选用的启发性信息有利于搜索效率的提高。但是理论上来讲，如果选用的启发性信息过强，则可能找不到最优解。

六、实验心得体会

第一次接触到A算法，第一次实验课的时候连花两节课去看算法的原理和计算过程，但还是没能充分理解。通过查阅资料，以及与同学深入探讨，仔细研究A算法之后，才明白程序如何编写，各部分的函数如何构成。同时，通过本次实验，发现选用不同的启发函数，对于实验的结果有较大的影响。正如表3-1所示，选用第一或第二种（也就是采用A*算法）远远优于普通的广度优先搜索，同时，明显的感觉到第二种启发函数效率更高，更快的找到最优解。总的来说，实践出真知，只有把书上的理论知识运用到实践，才是真正地掌握。

附录代码：

#include "iostream"  
#include "stdlib.h"  
#include "conio.h"  
#include <math.h>
#include <windows.h>
#define size 3  
using namespace std;
//定义二维数组来存储数据表示某一个特定状态  
typedef int status[size][size];
struct SpringLink;

//定义状态图中的结点数据结构  
typedef struct Node
{
   
    status data;//结点所存储的状态 ，一个3*3矩阵 
    struct Node* parent;//指向结点的父亲结点  
    struct SpringLink* child;//指向结点的后继结点  
    struct Node* next;//指向open或者closed表中的后一个结点  
    int fvalue;//结点的总的路径  
    int gvalue;//结点的实际路径  
    int hvalue;//结点的到达目标的困难程度  
}NNode, * PNode;


//定义存储指向结点后继结点的指针的地址  
typedef struct SpringLink
{
   
    struct Node* pointData;//指向结点的指针  
    struct SpringLink* next;//指向兄第结点  
}SPLink, * PSPLink;


PNode open;
PNode closed;
//OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点

//开始状态与目标状态  
/*
status startt = {1,3,0,8,2,4,7,6,5};最佳路径为2
status startt = {1,3,0,2,8,4,7,6,5};迭代超过20000次，手动停止
status startt = {2,8,3,1,6,4,7,0,5};
status startt = {2,8,3,6,0,4,1,7,5}; //实验报告
*/
int t = 0; //迭代次数,相当于运行时间 
int count_extendnode = 0;//扩展结点 
int count_sumnode = 0; //生成节点 
status startt = {
    2,8,3,6,0,4,1,7,5 }; //实验报告
status target = {
    1,2,3,8,0,4,7,6,5 };
//初始化一个空链表  
void initLink(PNode& Head)
{
   
    Head = (PNode)malloc(sizeof(NNode));
    Head->next = NULL;
}


//判断链表是否为空  
bool isEmpty(PNode Head)
{
   
    if (Head->next == NULL)
        return true;
    else
        return false;
}


//从链表中拿出一个数据  
void popNode(PNode& Head, PNode& FNode)
{
   
    if (isEmpty(Head))
    {
   
        FNode = NULL;
        return;
    }
    FNode = Head->next;
    Head->next = Head->next->next;
    FNode->next = NULL;
}



//向结点的最终后继结点链表中添加新的子结点  
void addSpringNode(PNode& Head, PNode newData)
{
   
    PSPLink newNode = (PSPLink)malloc(sizeof(SPLink));
    newNode->