数据挖掘课程实验 1：数据预处理

实验 1：数据预处理实验

一、实验目的及要求：

(1) 在学习的过程中，学生需要在教材的基础上搜索相关的文献资料，采用任何数据预处理方法，只要能达到相应的决策目的即视为有效。
(2) 对于研究内容，只要能够为以后的数据挖掘提供准备功能即可，同时对于研究方法也不做具体的限制，但是要能体现出数据预处理的合理性。

二、实验内容：

(1) 研究数据预处理方法。
(2) 编制出数据预处理方法的程序，并基于实例进行实现得出最终实验结果。

三、设备要求

(1) PC 一台。
(2) Python 或 C++或 JAVA 编程软件。

四、原始数据分析

1、数据来源
数据集为自行生成的。
2、脏数据类型
（1）缺失数据
导致数据缺失的原因有很多种，例如系统问题、人为问题等。假如出现了数据缺失情况，为了不影响数据分析结果的准确性，在数据分析时就需要进行补值，或者将空值排除在分析范围之外。
排除空值会减少数据分析的样本总量，这个时候可以选择性地纳入一些平均数、比例随机数等。若系统中还留有缺失数据的相关记录，可以通过系统再次引入，若系统中也没有这些数据记录，就只能通过补录或者直接放弃这部分数据来解决。
（2）重复数据
相同的数据出现多次的情况相对而言更容易处理，因为只需要去除重复数据即可。
（3）错误数据
错误数据一般是因为数据没有按照规定程序进行记录而出现的。对于异常值，可以通过限定区间的方法进行排除；对于格式错误，需要通过系统内部逻辑结构进行查找；对于数据不统一，无法从系统方面去解决，因为它并不属于真正的“错误”，系统并不能判断出天津和tianjin属于同一“事物”，因此只能通过人工干预的方法，做出匹配规则，用规则表去关联原始表。例如，一旦出现tianjin这个数据就直接匹配到天津。
（4）不可用数据
有些数据虽然正确但却无法使用。
五、算法分析


新数据加入可能导致最值变化，需要重新定义；
对奇异值(Outlier)非常敏感，因为其直接影响最值。故最值归一化只适用于数据在一个范围内分布而不会出现Outlier的情况。

4、连续值离散化
连续属性离散化(Discretization of Continuous Attributes)是指将连续数据分段为一系列离散化区间，每个区间对应一个属性值。连续属性离散化的主要原因如下：
算法要求，例如分类决策树等基于分类属性的算法；
连续属性离散化的主要方法阐述如下。
无监督离散方法：
等距离散化，即将连续属性划分为若干有限区间，每个区间长度相等。
等频离散化，即将连续属性划分为若干有限区间，每个区间样本数相同。
有监督离散方法：
信息增益法，是一种二分法(bi-partition)，核心是以离散前后信息增益最大的点为二分位点。
5、缺失值处理
侦测成本过高、隐私保护、无效数据、信息遗漏等情况都会造成实际应用时数据集属性缺失，因此缺失值处理不可避免。
缺失值处理的主要方式阐述如下：
插值填充，即用已有数据的分布来推测缺失值。例如均值填充(主要针对连续型属性)、众数填充(主要针对离散型属性)、回归填充(基于已有属性值建立回归方程估计缺失值)等。
相似填充，即用和缺失属性样本相似的若干样本推测缺失值。例如热卡填充(Hot Deck Imputation)，基于某种相似度度量选择数据集中与之最相似的样本属性代替缺失值；聚类填充，基于聚类分析选择数据集中与之最相似的样本子集进行插值填充。
C4.5方法，直接使用缺失属性样本，用加权方式衡量样本对结果的影响，主要用于决策树算法。

六、实验结果分析

1、实验设置
利用Jupyter Notebook编写python语言进行数据预处理分析。
2、参数设置
针对不同的数据预处理流程采用不同的数据集。
3、实验结果与分析
（1）缺失值处理
查看数据集中的确实值统计结果，结果如图1所示。图中可以看到每个数据是否为缺失值，是的为true，不是为false。

图1、缺失值统计结果
处理方法1：删除缺失值，结果如图2所示。可以看到缺失值数量为0。

图2、删除缺失值
处理方法2：填充或替换缺失值，结果如图3所示。

图3、填充/替换缺失值
处理方法3：缺失值插补，用均值或众数或中位数插补，结果如图4所示。

图4、缺失值插补
（2）异常值处理
方法一：调用3 原则，查看随机生成的数据集中存在多少异常值，并画出分布图查看异常值的分布情况，结果如图5所示。

图5、异常值显示
从图中可以看出，存在异常值28条，其在总的数据中的分布情况也是随机的。
方法二：利用箱型图分析，通过箱型图可以很直观的看出数据的离散分布情况，上四分位数与下四分位数的距离越小说明越集中，否则说明越分散，对于上下边缘来说是一样的。然后通过中位数偏向于上四分位数还是下四分位数可以来分析数据分布的偏向。箱形图还有一个优点是相对受异常值的影响比较小，能够准确稳定地描绘出数据的离散分布情况，会比较有利于数据的清洗。结果如图6所示。

图6、箱型图分析
3、数据标准化和归一化
（1）0-1标准化，对两列随机数，进行归一化，结果如图7所示。

图7、归一化结果
从图中可以看出数据已经被统一映射到[0,1]区间上。
（2）Z-score标准化，结果如图8所示。

图8、Z-score标准化
从图中可以看出，所有数据被映射到均值为0，方差为1的分布中，但并不限制在区间内。
4、数据连续属性离散化
方法一：等宽法，将连续属性划分为若干有限区间，每个区间长度相等。结果如图9所示。

图9、等宽法
方法二：等频法，将连续属性划分为若干有限区间，每个区间样本数相同。结果如图10所示。

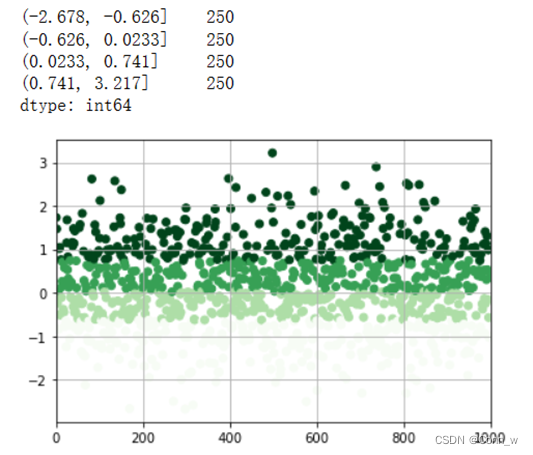
图10、等频法
从图中可以看出根据样本分位数对数据进行面元划分，得到大小基本相等的面元，但并不能保证每个面元含有相同数据个数。层次较为分明。
5、数据冗余
查看数据集中的重复数据，并对重复数据进行删除处理。结果如图11所示。

图11、数据冗余
6、表与表的连接
调用python中的merge函数，merge函数默认情况下，会按照相同字段的进行连接,其他参数一般用不到，主要只能两两拼接。结果如图12所示。

图12、表与表连接

七、实验总结

通过本次数据挖掘的预处理实验，了解了数据预处理的方法和主要步骤，依靠在教材的基础上查询网上的资料，学习了相关数据预处理的算法过程，并完成了对数据预处理方法的具体案例实现，基本掌握了数据预处理的主要过程，为未来的数据挖掘提供准备过程。

附：源代码
（1）缺失值处理

import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

s = pd.Series([12,33,45,23,np.nan,np.nan,66,54,np.nan,99])
df = pd.DataFrame({
   'value1':[12,33,45,23,np.nan,np.nan,66,54,np.nan,99,190],
                  'value2':['a','b','c','d','e',np.nan,np.nan,'f','g',np.nan,'g']})
#查看缺失值
print(s.isnull())
print(df.isnull().sum())

2、删除缺失值dropna

# 删除缺失值 - dropna
s.dropna(inplace=True)
df1=df[['value1','value2']].dropna()
print(df1.isnull().sum())

3