数据结构专题——动态树

动态树的概念

顾名思义，动态树是动态的，动态树维护了若干无序的有根树（实际上是无根的，操作过程中拓扑序不变）组成的森林.

动态树，支持树上的节点到根节点的操作（树链剖分能够维护的信息），同时动态树能够高效的实现换根、加减边、森林中树的合并分裂（这是树剖无法高效实现的），这里介绍的均为 $LCT(Link-CutTrees)$.

树链剖分一般指轻重链剖分，通过把树划分不同的链，然后在线段树上维护树上的信息；这里的 $LCT$ 是虚实链剖分，每个实链由一个 $Splay$ 维护.

可以说，$LCT$ 的实际结构就是由若干由虚边链接的伸展树组成的森林.

LCT 操作的时间复杂度

这里直接给出结论：

1. $LCA$ 每一次的操作的均摊时间复杂度为 $O(logN)$
2. 树链剖分的每一次的均摊时间复杂度为 $O(lo{g}^{2}N)$
3. 但树链剖分的常数比较小，$LCA$ 的常数较大

实链剖分

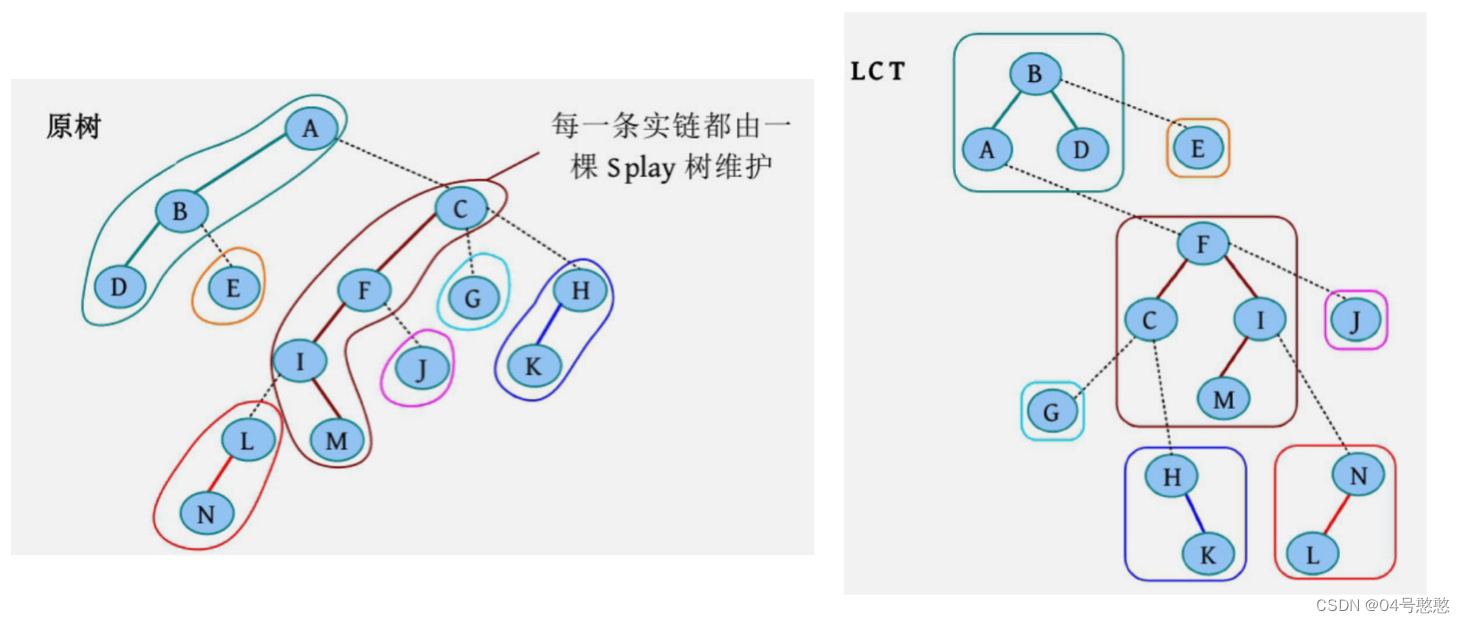
性质：

1. 一个节点到其子节点最多有一个实边，其他均为虚边
2. 每个伸展树维护一条按原树深度严格递增的实链
3. 每个节点都被包含且仅被包含在一颗伸展树
4. 重点：相邻伸展树之间，在表面上(原树)是通过最上面的节点之间相连；而在实际的数据结构中，相邻的伸展树之间 (即虚边)，是通过根节点的父节点
5. 虚边，认父不认子
6. 无论如何虚实变换、旋转，所有节点的相对位置都不变，即原树节点 $x-y$ 路径上没有节点 $z$，则操作完成以后，在 $x-y$ 路径上也不可能出现 $z$

例题 P3690【模板】动态树（Link Cut Tree）

题目描述

给定 $n$ 个点以及每个点的权值，要你处理接下来的 $m$ 个操作。
操作有四种，操作从 $0$ 到 $3$ 编号。点从 $1$ 到 $n$ 编号。

• 0 x y 代表询问从 $x$ 到 $y$ 的路径上的点的权值的 $\text{xor}$ 和。保证 $x$ 到 $y$ 是联通的。
• 1 x y 代表连接 $x$ 到 $y$，若 $x$ 到 $y$ 已经联通则无需连接。
• 2 x y 代表删除边 $(x,y)$，不保证边 $(x,y)$ 存在。
• 3 x y 代表将点 $x$ 上的权值变成 $y$。

输入格式

第一行两个整数，分别为 $n$ 和 $m$，代表点数和操作数。

接下来 $n$ 行，每行一个整数，第 $(i+1)$ 行的整数 $a_i$ 表示节点 $i$ 的权值。

接下来 $m$ 行，每行三个整数，分别代表操作类型和操作所需的量。

输出格式

对于每一个 $0$ 号操作，你须输出一行一个整数，表示 $x$ 到 $y$ 的路径上点权的 $\text{xor}$ 和。

样例 #1

样例输入 #1

3 3 
1
2
3
1 1 2
0 1 2 
0 1 1

样例输出 #1

3
1

样例 #2

样例输入 #2

5 14
114
514
19
19
810
1 1 2
0 1 2
2 1 2
1 1 2
1 2 3
2 1 3
1 1 3
1 4 5
1 2 5
0 3 5
0 3 4
3 5 233333
0 1 5
0 2 5

样例输出 #2

624
315
296
232709
232823

提示

数据规模与约定

对于全部的测试点，保证：

• $1\le n\le 10^5$，$1\le m\le 3\times 10^5$，$1\le a_i\le 10^9$。
• 对于操作 $0,1,2$，保证 $1\le x,y\le n$。
• 对于操作 $3$，保证 $1\le x\le n$，$1\le y\le 10^9$。

LCT 的核心操作

Splay类函数

1. pushup(x) ：在 Splay 旋转上更新节点的值，维护异或和

inline void pushup(int x)
{
	tr[x].sum=tr[tr[x].son[0]].sum^tr[tr[x].son[1]].sum^tr[x].val;
}

2. lazy(x)：打懒标记，注意懒标记的用法与线段树类似

inline void lazy(int x)
{
	swap(tr[x].son[0],tr[x].son[1]);
	tr[x].flag^=1;
}

3. pushdown(x)：下传懒标记

inline void pushdown(int x)
{
	if(!tr[x].flag)	 return;
	lazy(tr[x].son[0]),lazy(tr[x].son[1]);
	tr[x].flag=0;							//消除懒标记
}

4. rotate(x)：旋转函数，与Splay相同，向上旋

注意，在 $z$ 的旋转时，一定要注意不要破坏虚边的关系.

void rotate(int x)
{
	int y=tr[x].fa,z=tr[y].fa;
	int tag=tr[y].son[1]==x;
	tr[y].son[tag]=tr[x].son[tag^1],tr[tr[x].son[tag^1]].fa=y;
	tr[x].son[tag^1]=y,tr[y].fa=x;
	if(!isroot(y))	tr[z].son[tr[z].son[1]==y]=x;
	tr[x].fa=z;			//易错！！！，继承之前splay的根节点的父节点 
	pushup(y),pushup(x);
}

5. splay(x)：伸展操作函数

要注意，$Splay$操作，是要将较低处的节点往上翻滚，因此首先要将从根节点到目标节点的懒标记全部下传递，再逐层 $Splay$.

思考1：为什么在 $Splay$ 板题中，$Splay$ 前为什么不下传懒标记？
因为在板子题中，$Splay$ 操作之前，会在伸展树上找到区间的两个端点，这样在向上反转之前懒标记已经下传递，而在本题中却不一定，所以在 $Splay$ 之前要先用栈先下传懒标记.

void splay(int x)
{
	int ptr=0,y=x;
	stk[ptr++]=y;
	while(!isroot(y)) stk[ptr++]=tr[y].fa,y=tr[y].fa;	//栈处理 
	while(ptr--)	pushdown(stk[ptr]);			//下传懒标记
	while(!isroot(x))			//往上splay，直到x节点不为根节点， 
	{							//在朴素的 Splay 中，是判断x的父节点是否是0 
		int y=tr[x].fa,z=tr[y].fa;
		if(!isroot(y))			//在朴素的 Splay 的中，判断的是 z 是否是0 
			(tr[y].son[0]==x)^(tr[z].son[0]==y) ? rotate(x) : rotate(y);
		rotate(x);
	} 
}

LCT类操作

1. access(x)

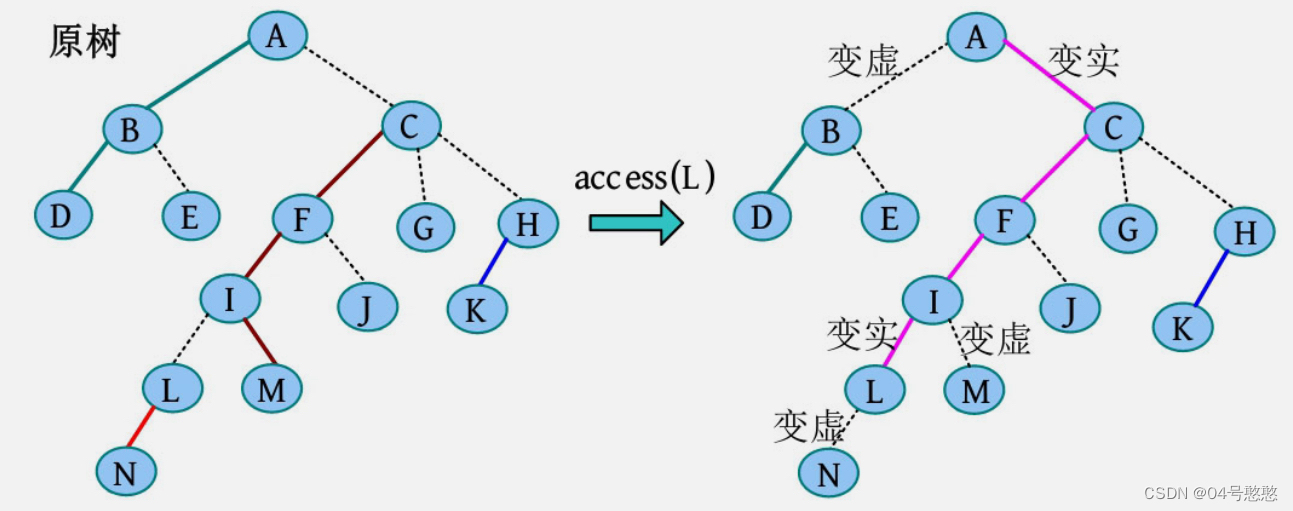
$access$ 操作是 $LCT$ 的核心操作，打通根节点到 $x$ 节点的路径，并使得 $x$ 的以下不再延申，同时使得 $x$ 成为 $Splay$ 的根节点.

void access(int x)
{
	int tp=x,y=0;
	
	while(x)			//整个树的根节点的父节点为 0 
	{
		splay(x);			//首先把 x 转到当前伸展树的根节点
		tr[x].son[1]=y;		//把下面的伸展树接到当前伸展树根节点的右节点
		pushup(x);			//更新当前节点
		y=x;
		x=tr[x].fa; 
	}
	
	splay(tp);
}

2. makeroot(x)

$makeroot$ 操作把 $x$ 节点调整到整个树的根节点，分为两个步骤：

1. $access(x)$ 首先打通根到 $x$ 的实链通路（$access$ 操作会同时将 $x$ 旋转到 $Splay$ 的根节点）
2. 由于 $x$ 是实链的最低端的节点，(因为根节点是最顶端，所以在 $Splay$ 中是树的最左端)，而当 $x$ 旋转到伸展树的根节点时，$x$ 的右子树为空！！！！！！
3. 所以，为了使得 $x$ 变成整个树的根节点，所以对整个树进行旋转，运用懒标记.

void makeroot(int x)
{
	access(x);
	lazy(x);	
} 

3. findroot(x)

$findroot(x)$ 的作用是找到 $x$ 所在树的根节点，并将目标节点（整个树的根节点）旋转到相应伸展树的根节点.

1. 首先，打通 $x$ 到根节点的实链 ( $access$ 操作会使得目标节点旋转到伸展树的根节点 )
2. 从伸展树的根节点 $x$ 一直往左查，最左便是原树的根节点，然后再将原树的根节点旋转到伸展树的根节点.

int findroot(int x)
{
	access(x);
	while(tr[x].son[0])	pushdown(x),x=tr[x].son[0];
	splay(x);
	return x;
} 

4.split(x,y)

$split(x,y)$ 操作的作用是打通 $x$ 到 $y$ 的实边路径，并且把 $y$ 旋转到伸展树的根节点.

void split(int x,int y)
{
	makeroot(x);
	access(y);
}

5. link(x,y)

若 $x,y$ 节点不连通，则链接 $x,y$；首先把 $x$ 变成原树的根节点，然后看 $y$ 的根节点是否是 $x$.

void link(int x,int y)
{
	makeroot(x);
	if(findroot(y)!=x)	tr[x].fa=y;
}

6. cut(x,y)

注意！注意！注意！这里的 $cut(x,y)$ 是指删除 $x,y$ 之间的边 (实边与虚边都可以删除)，即首先判断连通性，运用 $findroot(x)$ 判断；随后打通 $x,y$ 之间的实链，即 $split(x,y)$ 操作，操作后 $x$ 是原树根节点，然后判断原树的关系.

void cut(int x,int y)
{
	if(findroot(x)!=findroot(y))	return;
	split(x,y);
	if(tr[y].son[0]==x&&tr[x].son[1]==0)	tr[y].son[0]=0,tr[x].fa=0,pushup(x); 
} 

7. isroot(x)

判断 $x$ 是否是当前伸展树的根节点.

bool isroot(int x)		//认父不认子 
{
	return tr[tr[x].p].son[0]!=x && tr[tr[x].p].son[1]!=x;
}

整体代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<string>
#include<set>
#include<map>
#include<unordered_map>
#include<queue>

#define me(x,y) memset(x,y,sizeof x)
#define rep(i,x,y) for(i=x;i<=y;++i)
#define repf(i,x,y) for(i=x;i>=y;--i)
#define lowbit(x) -x&x
#define inf 0x3f3f3f3f
#define INF 0x7fffffff

using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> PII;

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

struct node
{
	int son[2],fa,val,sum;
	bool flag;
};

const int N= 1e5+10;
int n,m;

int stk[N];
node tr[N];

inline void pushup(int x)       //正确
{
	tr[x].sum=tr[tr[x].son[0]].sum^tr[tr[x].son[1]].sum^tr[x].val;
}

inline void lazy(int x)         //正确
{
	swap(tr[x].son[0],tr[x].son[1]);
	tr[x].flag^=1;
}

bool isroot(int x)		        //正确
{
	return tr[tr[x].fa].son[0]!=x && tr[tr[x].fa].son[1]!=x;
}

inline void pushdown(int x)     //正确
{
	if(!tr[x].flag)	 return;
	lazy(tr[x].son[0]),lazy(tr[x].son[1]);
	tr[x].flag=0;							//消除懒标记
}

void rotate(int x)
{
	int y=tr[x].fa,z=tr[y].fa;
	int tag=tr[y].son[1]==x;
	if(!isroot(y))	tr[z].son[tr[z].son[1]==y]=x;           //isroot判断必须在y更新的前面！！
	tr[x].fa=z;			//易错！！！，继承之前splay的根节点的父节点 
	tr[y].son[tag]=tr[x].son[tag^1],tr[tr[x].son[tag^1]].fa=y;
	tr[x].son[tag^1]=y,tr[y].fa=x;
	pushup(y),pushup(x);
}

void splay(int x)
{
	int ptr=0,y=x;
	stk[ptr++]=y;
	while(!isroot(y)) stk[ptr++]=tr[y].fa,y=tr[y].fa;	//栈处理 
	while(ptr--)	pushdown(stk[ptr]);			//下传懒标记
	while(!isroot(x))			//往上splay，直到x节点不为根节点， 
	{							//在朴素的 Splay 中，是判断x的父节点是否是0 
		int y=tr[x].fa,z=tr[y].fa;
		if(!isroot(y))			//在朴素的 Splay 的中，判断的是 z 是否是0 
			(tr[y].son[0]==x)^(tr[z].son[0]==y) ? rotate(x) : rotate(y);
		rotate(x);
	} 
}

void access(int x)
{
	int tp=x,y=0;
	
	while(x)			//整个树的根节点的父节点为 0 
	{
		splay(x);			//首先把 x 转到当前伸展树的根节点
		tr[x].son[1]=y;		//把下面的伸展树接到当前伸展树根节点的右节点
		pushup(x);			//更新当前节点
		y=x;
		x=tr[x].fa; 
	}
	
	splay(tp);
}

void makeroot(int x)
{
	access(x);
	lazy(x);	
}

int findroot(int x)
{
	access(x);
	while(tr[x].son[0])	pushdown(x),x=tr[x].son[0];
	splay(x);
	return x;
} 

void split(int x,int y)
{
	makeroot(x);
	access(y);
}

void link(int x,int y)
{
	makeroot(x);
	if(findroot(y)!=x)	tr[x].fa=y;
}

void cut(int x,int y)
{
	if(findroot(x)!=findroot(y))	return;
	split(x,y);
	if(tr[y].son[0]==x&&tr[x].son[1]==0)	tr[y].son[0]=0,tr[x].fa=0,pushup(x); 
} 

int main()
{
	int i,j,tag,x,y;
	
	n=read(),m=read();
	rep(i,1,n)	tr[i].val=read();
	
	while(m--)
	{
		tag=read(),x=read(),y=read();
		if(tag==0)
		{
			split(x,y);
			printf("%d\n",tr[y].sum);
		}
		else if(tag==1)     link(x,y);
		else if(tag==2)     cut(x,y);
		else		//因为要单点修改，所以根据Splay的性质，首先要把单点旋转到根节点 
		{
			splay(x);
			tr[x].val=y;
			pushup(x);
		}
	}
	
	return 0;
}