数论——同余，不定方程，CRT，高斯消元

同余

若两个整数 $a$，$b$ 除以 正整数 $m$ 后余数相同，则说 $a$，$b$ 关于模 $m$ 同余，记作：
$$a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$$

同余的相关性质：

1. 若 $a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m),c\equiv d(\mathrm{m}\mathrm{o}\mathrm{d}m)$，则 $a+c\equiv b+d(\mathrm{m}\mathrm{o}\mathrm{d}m)$
2. 若 $a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m),c\equiv d(\mathrm{m}\mathrm{o}\mathrm{d}m)$，则 $ac\equiv bd(\mathrm{m}\mathrm{o}\mathrm{d}m)$
3. 若 $a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$，则 $a^n\equiv b^n(\mathrm{m}\mathrm{o}\mathrm{d}m)$
4. 若 $a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$，则 $P(a)\equiv P(b)(\mathrm{m}\mathrm{o}\mathrm{d}m)$，$P$ 为任意多项式

易错点：
若 $ak\equiv bk(\mathrm{m}\mathrm{o}\mathrm{d}m)$，则不一定 $a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$

欧拉定理

表述：若正整数 $n$ 与整数 $a$ 互质，则满足 $a^{\varphi (n)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}n)$

当 $n\in primes$，则退化为费马小定理 $a^{n-1}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}n)$

费马小定理 是快速幂指数取模（mod-1），分数取模，求乘法逆元的依据.

整除性特征

1. 被 $4$ 和 $25$ 整除的特征是末二位数字能被 $4$ 或 $25$ 整除.
2. 被 $8$ 和 $125$ 整除的特征是末三位数字能被 $8$ 或 $125$ 整除.
3. 被 $9$ 整除的特征是各位数字和能被 $9$ 整除.
4. 被 $99$ 整除的特征是两位一段的所有数段和能被 $99$ 整除.

裴蜀定理

若 $a,b$ 是整数，且 $(a,b)=d$，则对于任意的整数 $x,y$，$ax+by$ 是 $d$ 的倍数.

裴蜀定理的作用：不定方程 $ax+by=c$ 有整数解，则 $(a,b)|c$

不定方程的通解（特解+齐次的通解）
设 $x_0,y_0$ 是方程 $ax+by=c$ 的一组整数解，则所有整数解为（通解）：
$$\{\begin{array}{l}x=x_0+\frac{b}{(a,b)}t\\ y=y_0-\frac{a}{(a,b)}t\end{array}$$

扩展欧几里得算法

本质裴蜀定理，直接上板子

ll exgcd(ll a,ll b,ll& x,ll& y)		//一定带引用
{
	if(!b)
	{
		x=1,y=0;
		return a;
	}
	
	ll d=exgcd(b,a%b,y,x);
	y-=a/b*x;
	
	return d;
} 

线性同余方程

例1：AcWing 878

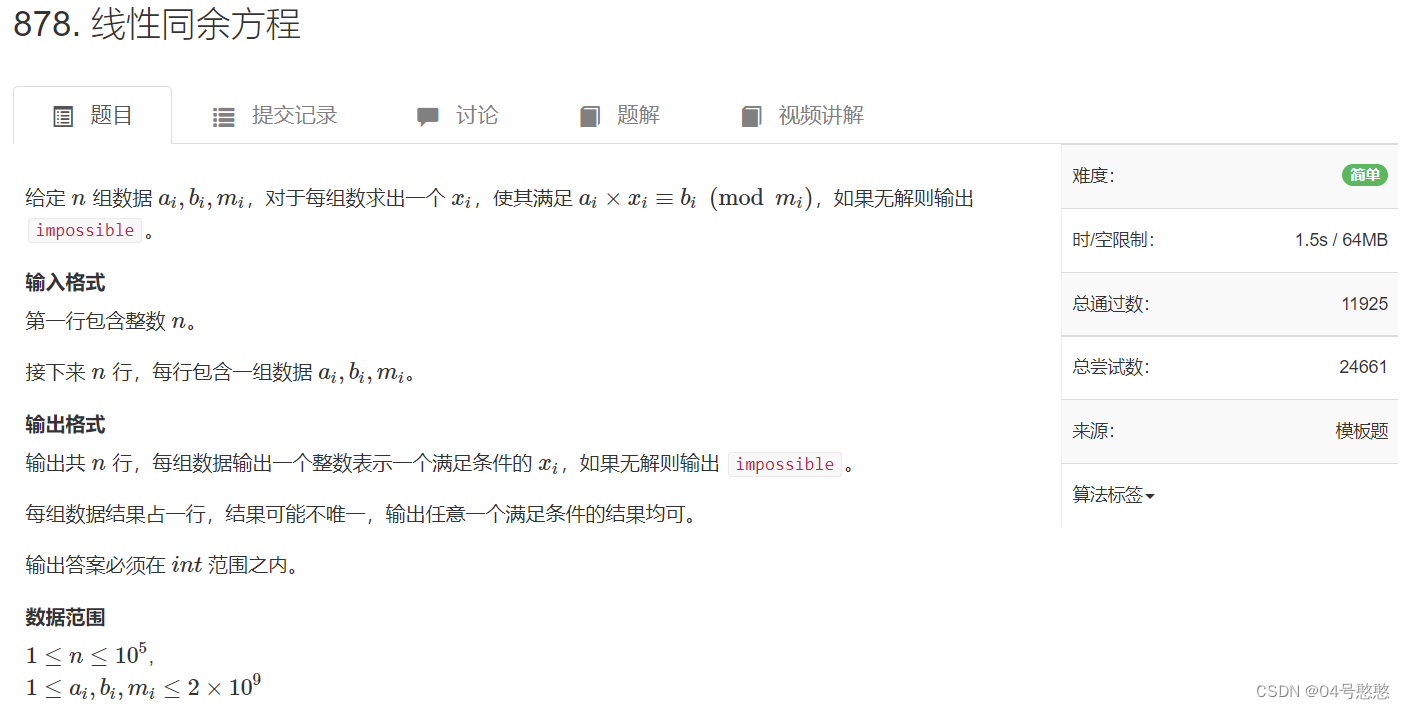
思路

本题的本质是解同余方程 $ax+my=b$，那么先解方程 $ax+my=gcd(a,m)$ （扩展欧几里得）
得到 $a{x}_0+m{y}_0=d$

首先判断 $d$ 是否整除 $b$

随后构造方程 $aX+mY=b$ 的形式，即
$$a(\frac{x_{0}b}{d})+m(\frac{y_{0}b}{d})=b$$

那么 $x$ 的通解就为 $x=\frac{x_{0}b}{d}+t|\frac{m}{d}|$

ll a,b,m;

ll exgcd(ll a,ll b,ll& x,ll& y)
{
	if(!b)
	{
		x=1,y=0;
		return a;
	}
	
	ll d=exgcd(b,a%b,y,x);
	y-=a/b*x;
	
	return d;
}

ll gcd(ll a,ll b)
{
	return b ? gcd(b,a%b) : a;
}

int main()
{
	int i,n;
	ll x,y,d,mod;
	
	n=read();
	while(n--)
	{
		a=read(),b=read(),m=read();
		d=exgcd(a,m,x,y);
		if(b%d)	puts("impossible");
		else
		{
		    x=x*b/d;
			mod=abs(m/d);
			printf("%lld\n",(x%mod+mod)%mod);
		}
	}
	
	return 0;
}

中国剩余定理

本质上就是解线性同余方程组.
就是一行一行解，要注意随时取模，防止溢出.

注意：$CRT$ 有解的条件是：模数两两互质

ll exgcd(ll a,ll b,ll& x,ll& y)
{
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    
    ll d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    
    return d;
}

int main()
{
	int i,n;
	ll a1,m1,a2,m2,a3,m3,x,y,d,mod;
	
	n=read();
	a1=read(),m1=read();
	
	rep(i,2,n)
	{
		a2=read(),m2=read();
		
		m2=(m2%a2+a2)%a2;
		
		d=exgcd(a1,-a2,x,y);
		if((m1-m2)%d)
		{
			printf("%d",-1);
			return 0;
		}
		
		x=(m1-m2)/d*x;
		x=(x%(a2/d)+a2/d)%(a2/d);
		
		a3=-a1*a2/d;
		m3=m1-a1*x;
		
		swap(a1,a3),swap(m1,m3);
		
		a1=abs(a1);                     //注意使得m变为正的
		m1=(m1%a1+a1)%a1;			    //使得 m 最小化 
	}
	
	printf("%lld",m1);
	
	return 0;
}

公式法求 $CRT$:

高斯消元

高斯消元，直接上板子

const int N=110;
const ld epsl=1e-8;
int n;

ld a[N][N];

int guass()
{
	int i,j,r=1,c,tp;
	
	rep(c,1,n)
	{
		tp=r;													/*****标准六部曲*****/ 
		rep(i,r+1,n)	if(fabs(a[i][c])>fabs(a[tp][c]))	tp=i;	//找主元
		if(fabs(a[tp][c])<epsl)	continue;							//若为0，继续 
		rep(i,c,n+1)	swap(a[tp][i],a[r][i]);						//交换 
		repf(i,n+1,c)	a[r][i]/=a[r][c];							//把主元变成1
		rep(i,r+1,n)	repf(j,n+1,c)	a[i][j]-=a[i][c]*a[r][j];	//用第一行去减下面的 icrj
		++r;														//别忘了 
	}
	
	if(r<c)
	{
		//检查接下来行的情况 
		rep(i,r,n)	if(fabs(a[i][n+1]>epsl))	return -1;
		return 0;	
	}
	
	repf(i,n,2)	repf(j,i-1,1)	a[j][n+1]-=a[i][n+1]*a[j][i]; //ji
	return 1;
}

int main()
{
	int i,j;
	
	n=read();
	rep(i,1,n)	rep(j,1,n+1)	scanf("%Lf",&a[i][j]);
	
	int res=guass();
	
	if(res==-1)	puts("No solution");
	else if(res==0) puts("Infinite group solutions");
	else	rep(i,1,n)	printf("%.2Lf\n",fabs(a[i][n+1])<epsl ? 0 : a[i][n+1]);
	
	return 0;
}