数论——约数与欧拉函数

约数性质

根据试除法的结论，一个整数 $N$ 的约数个数的上界为 $2\sqrt{N}$

约数个数定理，其中 $a_i$ 为质因子的次数（算术基本定理）：
$$\prod _{i=1}^n(a_i+1)$$

约数和定理（数学归纳法）：
$$\prod _{i=1}^n\sum _{j=0}^{a_i}{p}_i^j$$

$int$ 范围内，一个正整数最多的约数个数为 $1536$

试除法求约数板子（注意易错点）：

int getfactor(int x)
{
	int i;
	
	vector<int>ans;
	
	for(i=1;i<x/i;++i)
	{
		if(x%i==0)	ans.push_back(i),ans.push_back(x/i); 
	}
	
	if((ll)i*(ll)i==(ll)x)	ans.push_back(i);       //不能写 if(x%i==0)!!!!!
	
	sort(ans.begin(),ans.end());
	
	for(auto& x:ans)	printf("%d ",x);
	puts(""); 
}

欧拉函数(数论)的定义

对正整数n，欧拉函数是小于等于n的正整数中与n互质的数的数目

欧拉函数的性质（均正整数）

1. $1$ 的欧拉函数是 $1$
   $$\varphi (1)=1$$

2. 欧拉函数通项(证明：容斥原理)
   $$\varphi (N)=N\prod _{p\in primes}^{p|N}(1-\frac{1}{p})(N>1)$$

3. 欧拉函数是非完全积性函数(易证)，当 $gcd(m,n)=1$ 时：
   $$\varphi (mn)=\varphi (m)\varphi (n)$$

4. 若 $m\in N^{\ast }$ ($m$ 的约数的欧拉函数和等于 $m$):
   $$\sum _{d|m}\varphi (d)=\sum _{d|m}\varphi (\frac{m}{d})=m$$
   证明：
   设 $a\in [1,m],a\in N^{\ast }$，则 $a$ 可以取 $m$ 种值

   设 $d=gcd(a,m)$ ，则满足这个条件的 $a$ 有 $\varphi (\frac{m}{d})$ 个

   所以 $\sum \varphi (\frac{m}{d})=m$ (划分角度考虑)，证毕.

5. 当 $N>2$ 时，$$\varphi (N)\equiv 0(mod2)$$ 证明：
   当 $N>2$时：$$\varphi (N)=N(\frac{p_1-1}{p_1})(\frac{p_2-1}{p_2})...(\frac{p_k-1}{p_k})$$
   当 N ∈ { 2 c } N\in\{2^c\} N∈{2c}，很显然 $\varphi (N)$ 含有 $2$ 因子
   当 N ∉ { 2 c } N\notin\{2^c\} N∈/​{2c}，则一定存在一个奇质因子 $p_{odd}$，使得 $2|(p_{odd}-1)$，则 $2|\varphi (N)$
   证毕.

6. 当 $n\equiv 1(mod2)$ 时(易证)：$$\varphi (2n)=\varphi (n)$$

7. 对于 $x\in N^{\ast }，x>1$: $$\sum _{k=1}^{x-1}[gcd(k,x)=1]k=\frac{1}{2}x\varphi (x)$$ 证明：
   由欧几里得算法思想可知：$$gcd(x,k)=gcd(x,x-k)$$
   则对于满足 $gcd(k,x)=1$ 的 $k$ 与 $x-k$ ，一起贡献了 $x$ 的值，而不满足则不贡献，由于重复计算，所以要整体除以二，证毕.

8. 若 $m_1,m_2$ 有相同的质因子种类 ($m=m_1{m}_2$)(易证)：$$\varphi (m)=\varphi (m_1)m_2=\varphi (m_2)m_1$$

总结（引用自知乎）

例题

类型1：线性筛欧拉函数

题目传送门 Acwing 874

本题借助质数筛筛欧拉函数，时间复杂度 $O(N)$

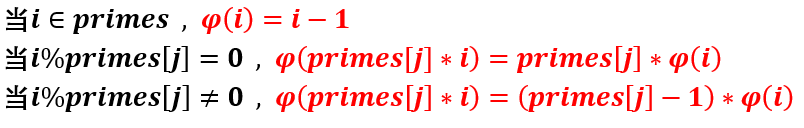
#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<string>
#include<set>
#include<map>
#include<unordered_map>
#include<queue>

#define mez(x) memset(x,0,sizeof x)
#define mei(x) memset(x,0x3f,sizeof x)
#define lowbit(x) -x&x
#define inf 0x3f3f3f3f
#define INF 0x7fffffff
#define cu(x) cout<<x<<"--"<<endl
#define ex exit(0)
#define pn puts("")

using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
typedef vector<int> vc;

const int N=1e6+10;
int n,cnt;
ll ans;

bool st[N];
int primes[N];
int phi[N];

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

ll get_phi()
{
    int i,j;
    
    phi[1]=1;
    for(i=2;i<=n;++i)
    {
        if(!st[i])  primes[cnt++]=i,phi[i]=i-1;
        for(j=0;primes[j]<=n/i;++j)
        {
            st[i*primes[j]]=true;
            
            if(i%primes[j]==0)
            {
                phi[i*primes[j]]=phi[i]*primes[j];
                break;
            }
            else
                phi[i*primes[j]]=phi[i]*(primes[j]-1);
        }
    }
    for(i=1;i<=n;++i)   ans+=phi[i];
    return ans;
}

int main()
{
    scanf("%d",&n);
    
    printf("%lld",get_phi());
	
	return 0;
}

类型2：互质对的个数统计

题目传送门 Acwing 220

本题的本质是统计 $1-N(N>0)$ 之间互质对的个数：$$-1+2\sum _{k=1}^N\varphi (k)$$
由质数分布，本题应当从质数的角度去枚举个数，时间复杂度 $O(N+\frac{N}{ln(N)})=O(N)$
当$$gcd(x,y)=p(p\in primes)$$
$$gcd(\frac{x}{p},\frac{y}{p})=1$$
则质数 $p$ 的贡献数量为 ：$$-1+2\sum _{k=1}^{\lfloor \frac{N}{p}\rfloor }\varphi (k)$$
所以答案为：
$$\sum _{p\in primes}^{p|N}(-1+2\sum _{k=1}^{\lfloor \frac{N}{p}\rfloor }\varphi (k))$$
所以本题的核心步骤是筛质数和维护欧拉函数前缀和，注意LL

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<string>
#include<set>
#include<map>
#include<unordered_map>
#include<queue>

#define mez(x) memset(x,0,sizeof x)
#define mei(x) memset(x,0x3f,sizeof x)
#define lowbit(x) -x&x
#define inf 0x3f3f3f3f
#define INF 0x7fffffff
#define cu(x) cout<<x<<"--"<<endl
#define ex exit(0)
#define pn puts("")

using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
typedef vector<int> vc;

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

const int N=1e7+10;
int n,cnt;

bool st[N];
int primes[N];
ll phi[N];

void get_primes()
{
    int i,j;
    
    phi[1]=1;
    for(i=2;i<=n;++i)
    {
        if(!st[i])  primes[cnt++]=i,phi[i]=i-1;
        for(j=0;primes[j]<=n/i;++j)
        {
            st[primes[j]*i]=true;
            if(i%primes[j]==0)
            {
                phi[i*primes[j]]=phi[i]*primes[j];
                break;
            }
            else
                phi[i*primes[j]]=phi[i]*(primes[j]-1);
        }
    }
    
    for(i=1;i<=n;++i)
        phi[i]+=phi[i-1];
}

int main()
{
    int i,j;
    ll ans=0;
    
    scanf("%d",&n);
    
    get_primes();
    
    for(i=0;i<cnt;++i)
        ans+=(-1LL+2LL*phi[n/primes[i]]);
    
    printf("%lld",ans);
	
	return 0;
}

类型3：欧拉函数积性的运用

题目传送门 POJ2480

本题的本质是求: $$f(N)=\sum _{i=1}^{N}gcd(i,N)$$
首先，肯定不能暴力求。按照上一个题的思想，从 $N$ 的约数入手，对于 $M,M|N$，设：
$$gcd(i^{\prime },N)=M(i^{\prime }\ge M)$$
那么，满足条件的 $i^{\prime }$ 的个数怎么求? 先对 $i^{\prime }$ 和 $N$ 分解：
$$i^{\prime }=M\ast j,N=M\ast j^{\prime }$$
很明显，满足条件的 $i^{\prime }$ 的个数为 $\varphi (\frac{N}{M})$，所以约数 $M$ 对答案的贡献为 $M\varphi (\frac{N}{M})$
本题的结果呼之欲出：
$$f(N)=\sum _{d|N}d\varphi (\frac{N}{d})$$
若根据上式直接求解，时间复杂度 $O(\sqrt{N})$，我们可以利用欧拉函数的积性优化时间，下面我们来探讨 $f(N)$ 的积性：
不妨设：$$f(n)=\sum _{d_1|n}{d}_1\varphi (\frac{n}{d_1}),f(m)=\sum _{d_2|m}{d}_2\varphi (\frac{m}{d_2})$$
由乘法分配律和欧拉函数的积性易得：$$f(n)f(m)=\sum _{d|nm}d\varphi (\frac{nm}{d})$$
所以：$f(N)$ 也为积性函数
由算数基本定理，可以对 $N$ 进行分解：
$$N=p_1^{c_1}{p}_2^{c_2}....p_k^{c_k}(p_i\in primes)$$
$$f(N)=f(p_1^{c_1}{p}_2^{c_2}....p_k^{c_k})$$
以其中一个为例子
$$f(p^c)=\sum _{i=0}^c{p}^i\varphi (\frac{p^c}{p^i})=p^c\varphi (1)+\sum _{i=0}^{c-1}{p}^i\varphi (\frac{p^c}{p^i})$$
$$\sum _{i=0}^{c-1}{p}^i\varphi (\frac{p^c}{p^i})=\sum _{i=0}^{c-1}{p}^i(p^{c-i})(1-\frac{1}{p})=\sum _{i=0}^{c-1}{p}^c-p^{c-1}=c(p^c-p^{c-1})$$
$$f(p^c)=(c+1)p^c-c{p}^{c-1}$$
最终可得：
$$f(N)=\prod _{p\in primes}^{p|N}((c+1)p^c-c{p}^{c-1})$$
所以，欧拉函数在本题中只是个过渡作用，本质是分解质因数+快速幂

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<string>
#include<set>
#include<map>
//#include<unordered_map>
#include<queue>

#define mez(x) memset(x,0,sizeof x)
#define mei(x) memset(x,0x3f,sizeof x)
#define lowbit(x) -x&x
#define inf 0x3f3f3f3f
#define INF 0x7fffffff
#define cu(x) cout<<x<<"--"<<endl
#define ex exit(0)
#define pn puts("")

using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
typedef vector<int> vc;

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

ll qmi(ll a,ll b)
{
	ll ans=1;
	
	while(b)
	{
		if(b&1)	ans*=a;
		a*=a;
		b>>=1;
	}
	
	return ans;
}

ll get_ans(ll target)
{
	ll i,nums,ans=1,temp;
	
	for(i=2;i*i<=target;++i)
	{
		if(target%i==0)
		{
			nums=0;
			while(target%i==0)	target/=i,++nums;
			temp=qmi(i,nums);
			ans*=(nums+1)*temp-nums*(temp/i);
		}
	}
	
	if(target>1)	ans*=2*target-1;
	
	return ans;
}

int main()
{
	ll n;
	
	while(~scanf("%lld",&n))
		printf("%lld\n",get_ans(n));	
	
	return 0;
}

附加：

求解 $$g(N)=\sum _{i=1}^{N}lcm(i,N)$$
本题和上题类似，就是公式推导过程中由些许不同：
类似地，我们还是从约数的角度出发，设 $M$ 是 $N$ 的约数，设 $gcd(i^{\prime },N)=M$：
$$i^{\prime }=M\ast j,N=M\ast j^{\prime }$$
可得约数 $M$ 的贡献值为：
$$\sum \frac{i^{\prime }N}{M}=N\sum j=N\ast (\frac{1}{2}{j}^{\prime }\varphi (j^{\prime }))(M\ne N)$$
(注意：为什么 $M\ne N$ ? 因为求和公式的条件是 $j^{\prime }>1$,所以最后要把 $M=N$的贡献单独加上)
所以可得：
$$g(N)=N+\frac{N}{2}\sum _{d|N,d\ne N}\frac{N}{d}\varphi (\frac{N}{d})$$
转化一下：
$$g(N)=N+\frac{N}{2}\sum _{d|N,d\ne 1}d\varphi (d)$$
若 直接枚举约数的话（时间复杂度$O(\sqrt{N})$）
namo:

由于int范围内的最多约数个数是1536，所以可以分解质因数后约束搜索一下，虽然理论复杂度差不多，但明显效率快好几倍…

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
#include<string>
#include<set>
#include<map>
#include<unordered_map>
#include<queue>

#define mez(x) memset(x,0,sizeof x)
#define mei(x) memset(x,0x3f,sizeof x)
#define lowbit(x) -x&x
#define inf 0x3f3f3f3f
#define INF 0x7fffffff
#define cu(x) cout<<x<<"--"<<endl
#define ex exit(0)
#define pn puts("")

using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
typedef vector<int> vc;

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

const int N=1e6,M=1600;
int t,cnt,idx,nums; 

ll primes[N+3],phi[N+3],p[M],q[M],fa[M];
bool st[N+3];

void get_primes()
{
	ll i,j;
	
	phi[1]=1;
	for(i=2;i<=N;++i)
	{
		if(!st[i])	primes[cnt++]=i,phi[i]=i-1;
		for(j=0;primes[j]<=N/i;++j)
		{
			st[primes[j]*i]=true;
			if(i%primes[j]==0)
			{
				phi[i*primes[j]]=phi[i]*primes[j];
				break;
			}
			else
				phi[i*primes[j]]=phi[i]*(primes[j]-1);
		}
	}
}

inline void get_factor(int t)
{
	ll i,j;
	
	for(i=2;i<=t/i;++i)
	{
		if(t%i==0)
		{
			j=0;
			while(t%i==0) t/=i,++j;
			p[idx]=i;
			q[idx++]=j;
		}
	}
	if(t>1)	p[idx]=t,q[idx++]=1;
}

void dfs(int i,int now)
{
	if(i==idx)
	{
		fa[nums++]=now;
		return;
	}
	
	int k;
	
	for(k=0;k<=q[i];++k,now*=p[i])
		dfs(i+1,now);
}

ll get_ans(ll t)
{
	ll temp=0;
	nums=idx=0;
	
	get_factor(t);
	dfs(0,1);
	
	for(int i=1;i<nums;++i)
		temp+=fa[i]*phi[fa[i]];
	temp=temp*t/2;
	temp+=t;
	
	return temp;
}

int main()
{
	int temp;
	
	get_primes();
	
	t=read();
	while(t--)
	{
		temp=read();
		if(temp<=0)	printf("%d\n",0);
		else	printf("%lld\n",get_ans((ll)temp));
	}
	
	return 0;
}

未完待续