机器学习实战 —— 工业蒸汽量预测（总）-CSDN博客

本文链接：https://blog.csdn.net/m0_53054984/article/details/138189384

本文详细介绍了如何运用机器学习技术预测工业蒸汽量，涵盖数据分析、特征工程、模型训练和验证等多个步骤。通过数据探索，识别关键变量，进行异常值处理、归一化和特征降维。利用多元线性回归、KNN、决策树、随机森林、lightgbm等模型进行训练，并通过交叉验证和模型融合提升预测精度。最后，通过Stacking进行模型融合，以提高预测效果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

🌟欢迎来到 我的博客 —— 探索技术的无限可能！

🌟博客的简介（文章目录）

文章描述

数据分析：查看变量间相关性以及找出关键变量。
机器学习实战 —— 工业蒸汽量预测（一）
数据特征工程对数据精进：异常值处理、归一化处理以及特征降维。
机器学习实战 —— 工业蒸汽量预测（二）
模型训练(涉及主流ML模型)：决策树、随机森林，lightgbm等。
机器学习实战 —— 工业蒸汽量预测（三）
模型验证：评估指标以及交叉验证等。
机器学习实战 —— 工业蒸汽量预测（四）
特征优化：用lgb对特征进行优化。
机器学习实战 —— 工业蒸汽量预测（五）
模型融合：进行基于stacking方式模型融合。
机器学习实战 —— 工业蒸汽量预测（六）

背景描述

背景介绍

火力发电的基本原理是：燃料在燃烧时加热水生成蒸汽，蒸汽压力推动汽轮机旋转，然后汽轮机带动发电机旋转，产生电能。在这一系列的能量转化中，影响发电效率的核心是锅炉的燃烧效率，即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多，包括锅炉的可调参数，如燃烧给量，一二次风，引风，返料风，给水水量；以及锅炉的工况，比如锅炉床温、床压，炉膛温度、压力，过热器的温度等。

相关描述

经脱敏后的锅炉传感器采集的数据（采集频率是分钟级别），根据锅炉的工况，预测产生的蒸汽量。

结果评估

预测结果以mean square error作为评判标准。

数据说明

数据分成训练数据（train.txt）和测试数据（test.txt），其中字段”V0”-“V37”，这38个字段是作为特征变量，”target”作为目标变量。选手利用训练数据训练出模型，预测测试数据的目标变量，排名结果依据预测结果的MSE（mean square error）。

数据来源

http://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/Industrial_Steam_Forecast/zhengqi_test.txt
http://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/Industrial_Steam_Forecast/zhengqi_train.txt

实战内容

1.数据分析

导入模块

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from scipy import stats

import warnings
warnings.filterwarnings("ignore")
 
%matplotlib inline

读取数据文件
使用Pandas库read_csv()函数进行数据读取，分割符为‘\t’

train_data_file = "./zhengqi_train.txt"
test_data_file =  "./zhengqi_test.txt"

train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')

1.1 查看数据信息

查看特征变量信息

train_data.info()

在这里插入图片描述

可以看到训练集数据共有2888个样本，数据中有V0-V37共计38个特征变量，变量类型都为数值类型，所有数据特征没有缺失值数据。

数据字段由于采用了脱敏处理，删除了特征数据的具体含义。其中target字段为标签变量。

test_data.info()

在这里插入图片描述

测试集数据共有1925个样本，数据中有V0-V37共计38个特征变量，变量类型都为数值类型

查看数据统计信息：

train_data.describe()

在这里插入图片描述

test_data.describe()

在这里插入图片描述

上面数据显示了数据的统计信息，例如样本数，数据的均值mean，标准差std，最小值，最大值等

查看数据字段信息：

train_data.head()

在这里插入图片描述

test_data.head()

在这里插入图片描述

1.2 可视化探索数据

在这里插入图片描述

箱式图

在这里插入图片描述

查看数据分布图

查看特征变量‘V0’的数据分布直方图，并绘制Q-Q图查看数据是否近似于正态分布

在这里插入图片描述

查看查看所有数据的直方图和Q-Q图，查看训练集的数据是否近似于正态分布

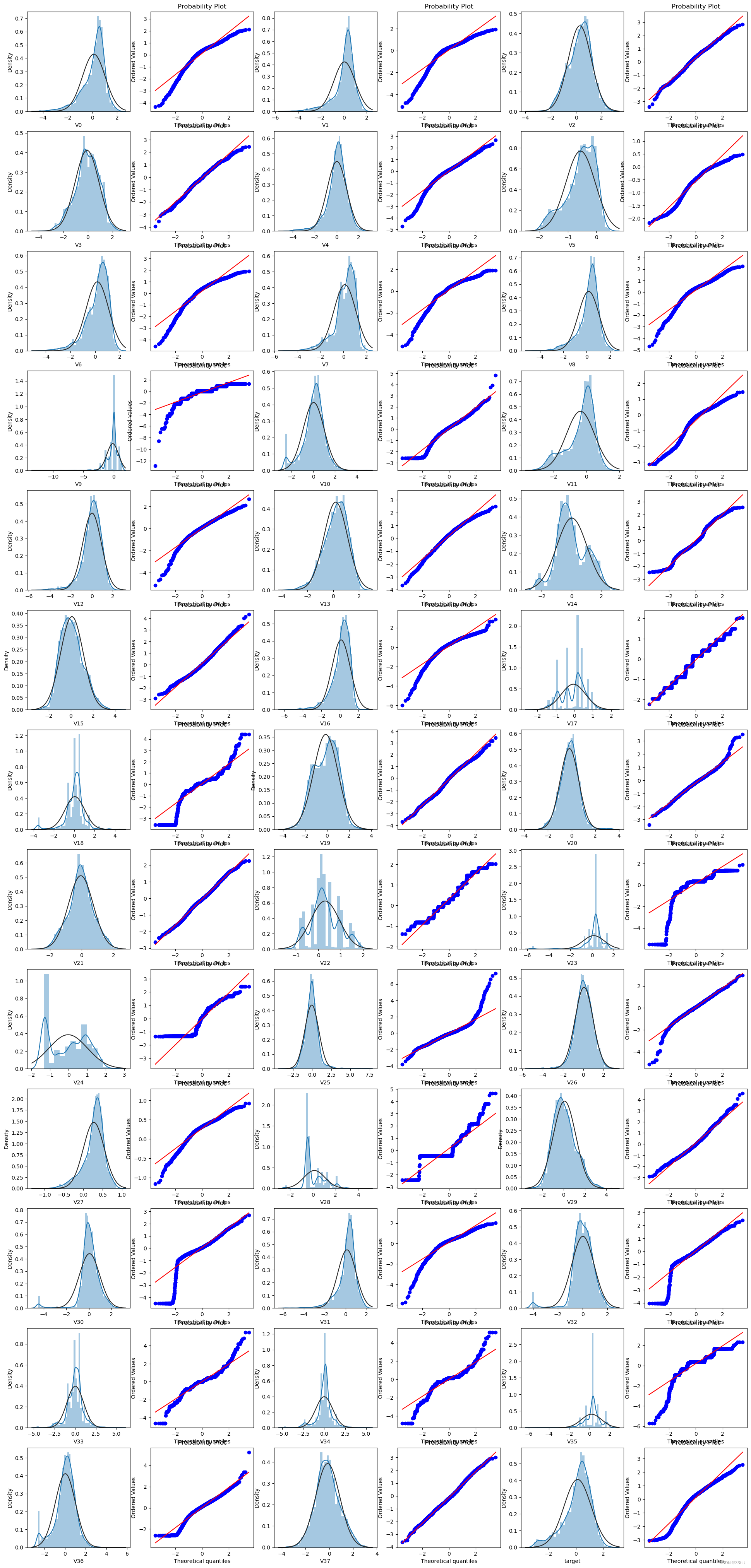
在这里插入图片描述

由上面的数据分布图信息可以看出，很多特征变量（如’V1’,‘V9’,‘V24’,'V28’等）的数据分布不是正态的，数据并不跟随对角线，后续可以使用数据变换对数据进行转换。

对比同一特征变量‘V0’下，训练集数据和测试集数据的分布情况，查看数据分布是否一致

在这里插入图片描述

查看所有特征变量下，训练集数据和测试集数据的分布情况，分析并寻找出数据分布不一致的特征变量。

在这里插入图片描述

查看特征’V5’, ‘V17’, ‘V28’, ‘V22’, ‘V11’, 'V9’数据的数据分布

在这里插入图片描述

由上图的数据分布可以看到特征’V5’,‘V9’,‘V11’,‘V17’,‘V22’,‘V28’ 训练集数据与测试集数据分布不一致，会导致模型泛化能力差，采用删除此类特征方法。

# 合并训练集和测试集数据，并可视化训练集和测试集数据特征分布图
drop_columns = ['V5','V9','V11','V17','V22','V28']

可视化线性回归关系

查看特征变量‘V0’与’target’变量的线性回归关系

在这里插入图片描述

1.2.1 查看变量间线性回归关系

在这里插入图片描述

1.2.2 查看特征变量的相关性

data_train1 = train_data.drop(['V5','V9','V11','V17','V22','V28'],axis=1)
train_corr = data_train1.corr()
train_corr

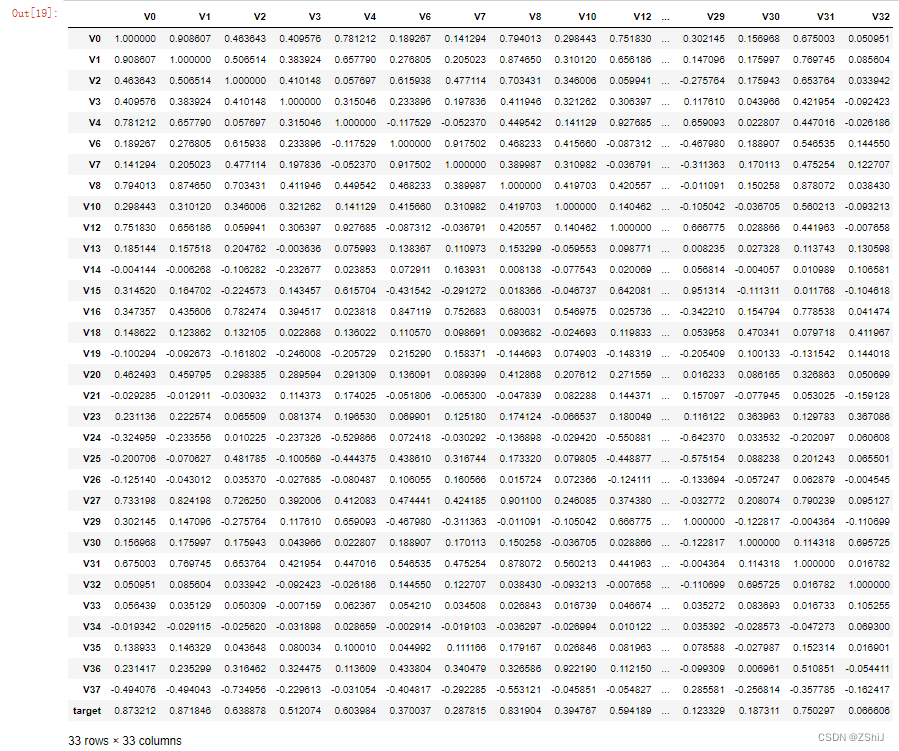
在这里插入图片描述

1.2.3 查找重要变量

查找出特征变量和target变量相关系数大于0.5的特征变量

寻找K个最相关的特征信息

在这里插入图片描述

drop_columns.clear()
drop_columns = ['V5','V9','V11','V17','V22','V28']
threshold = 0.5
corr_matrix = data_train1.corr().abs()
drop_col=corr_matrix[corr_matrix["target"]<threshold].index

由于’V14’, ‘V21’, ‘V25’, ‘V26’, ‘V32’, ‘V33’, 'V34’特征的相关系数值小于0.5，故认为这些特征与最终的预测target值不相关，删除这些特征变量；

train_x =  train_data.drop(['target'], axis=1)
data_all = pd.concat([train_x,test_data]) 
data_all.drop(drop_columns,axis=1,inplace=True)
data_all.head()

在这里插入图片描述

cols_numeric=list(data_all.columns)
def scale_minmax(col):
    return (col-col.min())/(col.max()-col.min())

data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax,axis=0)
data_all[cols_numeric].describe()

在这里插入图片描述

train_data_process = train_data[cols_numeric]
train_data_process = train_data_process[cols_numeric].apply(scale_minmax,axis=0)

test_data_process = test_data[cols_numeric]
test_data_process = test_data_process[cols_numeric].apply(scale_minmax,axis=0)

cols_numeric_left = cols_numeric[0:13]
cols_numeric_right = cols_numeric[13:]

图1

在这里插入图片描述

图2

在这里插入图片描述

2.数据特征工程

2.1数据预处理和特征处理

导入包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from scipy import stats

import warnings
warnings.filterwarnings("ignore")
 
%matplotlib inline

# 读取数据
train_data_file = "./zhengqi_train.txt"
test_data_file =  "./zhengqi_test.txt"

train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')

数据总览

train_data.describe()

在这里插入图片描述

2.1.1 异常值分析

异常值分析

在这里插入图片描述

删除异常值

train_data = train_data[train_data['V9']>-7.5]
train_data.describe()

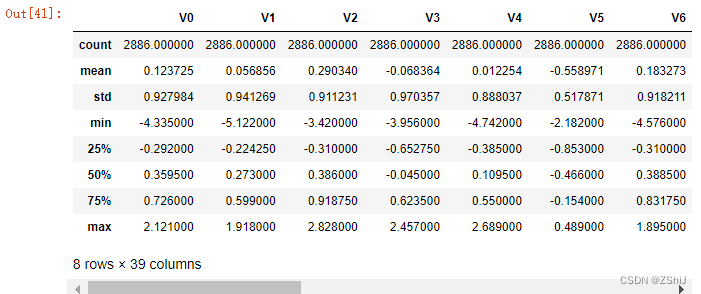
在这里插入图片描述

test_data.describe()

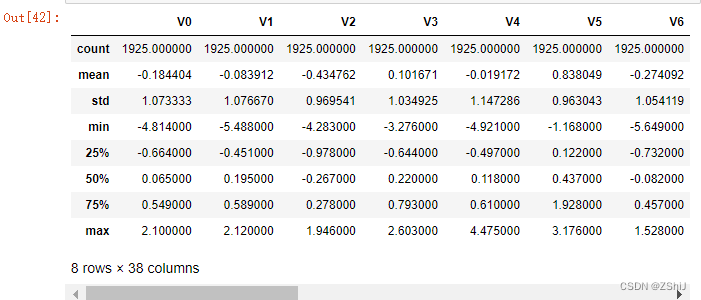
在这里插入图片描述

2.1.2 归一化处理

from sklearn import preprocessing 

features_columns = [col for col in train_data.columns if col not in ['target']]

min_max_scaler = preprocessing.MinMaxScaler()

min_max_scaler = min_max_scaler.fit(train_data[features_columns])

train_data_scaler = min_max_scaler.transform(train_data[features_columns])
test_data_scaler = min_max_scaler.transform(test_data[features_columns])

train_data_scaler = pd.DataFrame(train_data_scaler)
train_data_scaler.columns = features_columns

test_data_scaler = pd.DataFrame(test_data_scaler)
test_data_scaler.columns = features_columns

train_data_scaler['target'] = train_data['target']

train_data_scaler.describe()

test_data_scaler.describe()

在这里插入图片描述

查看数据集情况

在这里插入图片描述

查看特征’V5’, ‘V17’, ‘V28’, ‘V22’, ‘V11’, 'V9’数据的数据分布

在这里插入图片描述

这几个特征下，训练集的数据和测试集的数据分布不一致，会影响模型的泛化能力，故删除这些特征

2.1.3 特征相关性

在这里插入图片描述

2.2 特征降维

mcorr=mcorr.abs()
numerical_corr=mcorr[mcorr['target']>0.1]['target']
print(numerical_corr.sort_values(ascending=False))

index0 = numerical_corr.sort_values(ascending=False).index
print(train_data_scaler[index0].corr('spearman'))

在这里插入图片描述

2.2.1 相关性初筛

features_corr = numerical_corr.sort_values(ascending=False).reset_index()
features_corr.columns = ['features_and_target', 'corr']
features_corr_select = features_corr[features_corr['corr']>0.3] # 筛选出大于相关性大于0.3的特征
print(features_corr_select)
select_features = [col for col in features_corr_select['features_and_target'] if col not in ['target']]
new_train_data_corr_select = train_data_scaler[select_features+['target']]
new_test_data_corr_select = test_data_scaler[select_features]

在这里插入图片描述

2.2.2 多重共线性分析

# !pip install statsmodels -i https://pypi.tuna.tsinghua.edu.cn/simple

from statsmodels.stats.outliers_influence import variance_inflation_factor #多重共线性方差膨胀因子

#多重共线性
new_numerical=['V0', 'V2', 'V3', 'V4', 'V5', 'V6', 'V10','V11', 
                         'V13', 'V15', 'V16', 'V18', 'V19', 'V20', 'V22','V24','V30', 'V31', 'V37']
X=np.matrix(train_data_scaler[new_numerical])
VIF_list=[variance_inflation_factor(X, i) for i in range(X.shape[1])]
VIF_list

在这里插入图片描述

2.2.3 PCA处理降维

from sklearn.decomposition import PCA   #主成分分析法

#PCA方法降维
#保持90%的信息
pca = PCA(n_components=0.9)
new_train_pca_90 = pca.fit_transform(train_data_scaler.iloc[:,0:-1])
new_test_pca_90 = pca.transform(test_data_scaler)
new_train_pca_90 = pd.DataFrame(new_train_pca_90)
new_test_pca_90 = pd.DataFrame(new_test_pca_90)
new_train_pca_90['target'] = train_data_scaler['target']
new_train_pca_90.describe()

在这里插入图片描述

train_data_scaler.describe()

在这里插入图片描述

PCA方法降维

保留16个主成分

pca = PCA(n_components=0.95)
new_train_pca_16 = pca.fit_transform(train_data_scaler.iloc[:,0:-1])
new_test_pca_16 = pca.transform(test_data_scaler)
new_train_pca_16 = pd.DataFrame(new_train_pca_16)
new_test_pca_16 = pd.DataFrame(new_test_pca_16)
new_train_pca_16['target'] = train_data_scaler['target']
new_train_pca_16.describe()

在这里插入图片描述

3.模型训练

3.1 回归及相关模型

# !pip install lightgbm

导入包

from sklearn.linear_model import LinearRegression  #线性回归
from sklearn.neighbors import KNeighborsRegressor  #K近邻回归
from sklearn.tree import DecisionTreeRegressor     #决策树回归
from sklearn.ensemble import RandomForestRegressor #随机森林回归
from sklearn.svm import SVR  #支持向量回归
import lightgbm as lgb #lightGbm模型
from sklearn.ensemble import GradientBoostingRegressor

from sklearn.model_selection import train_test_split # 切分数据
from sklearn.metrics import mean_squared_error #评价指标

from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit

## 切分训练数据和线下验证数据

#采用 pca 保留16维特征的数据
new_train_pca_16 = new_train_pca_16.fillna(0)
train = new_train_pca_16[new_test_pca_16.columns]
target = new_train_pca_16['target']

# 切分数据 训练数据80% 验证数据20%
train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)

3.1.1 多元线性回归模型

在这里插入图片描述

定义绘制模型学习曲线函数

def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
                        n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
    plt.figure()
    plt.title(title)
    if ylim is not None:
        plt.ylim(*ylim)
    plt.xlabel("Training examples")
    plt.ylabel("Score")
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    print(train_scores_mean)
    print(test_scores_mean)
    
    plt.grid()
 
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,
                     color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1, color="g")
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
             label="Training score")
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")
 
    plt.legend(loc="best")
    return plt

绘制学习曲线：只需要传入算法(或实例对象)、X_train、X_test、y_train、y_test

当使用该函数时传入算法，该算法的变量要进行实例化，如：PolynomialRegression(degree=2)，变量 degree 要进行实例化

def plot_learning_curve_old(algo, X_train, X_test, y_train, y_test):

    train_score = []
    test_score = []
    for i in range(10, len(X_train)+1, 10):
        algo.fit(X_train[:i], y_train[:i])
        
        y_train_predict = algo.predict(X_train[:i])
        train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
        y_test_predict = algo.predict(X_test)
        test_score.append(mean_squared_error(y_test, y_test_predict))
    
    plt.plot([i for i in range(1, len(train_score)+1)],
            train_score, label="train")
    plt.plot([i for i in range(1, len(test_score)+1)],
            test_score, label="test")
    
    plt.legend()
    plt.show()

在这里插入图片描述

线性回归模型学习曲线
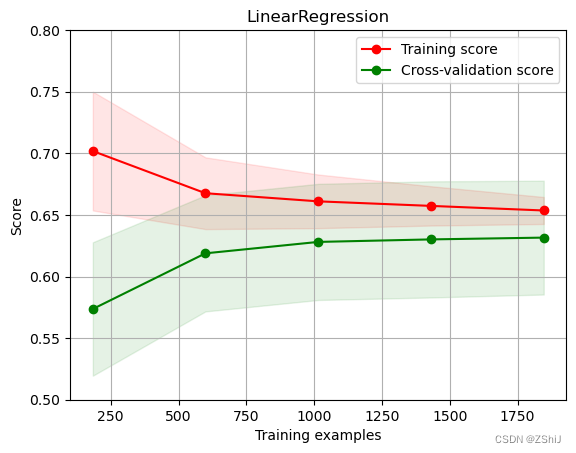
在这里插入图片描述

3.1.2 KNN近邻回归

for i in range(3,10):
    clf = KNeighborsRegressor(n_neighbors=i) # 最近三个
    clf.fit(train_data, train_target)
    score = mean_squared_error(test_target, clf.predict(test_data))
    print("KNeighborsRegressor:   ", score)

在这里插入图片描述

在这里插入图片描述
绘制K近邻回归学习曲线——K近邻回归

在这里插入图片描述

3.1.3决策树回归

clf = DecisionTreeRegressor() 
clf.fit(train_data, train_target)
score = mean_squared_error(test_target, clf.predict(test_data))
print("DecisionTreeRegressor:   ", score)

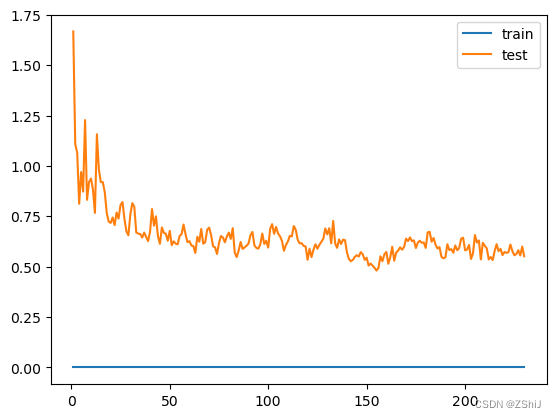
在这里插入图片描述

决策树回归
在这里插入图片描述

3.1.4 随机森林回归

clf = RandomForestRegressor(n_estimators=200) # 200棵树模型
clf.fit(train_data, train_target)
score = mean_squared_error(test_target, clf.predict(test_data))
print("RandomForestRegressor:   ", score)
# plot_learning_curve_old(RandomForestRegressor(n_estimators=200), train_data, test_data, train_target, test_target)

X = train_data.values
y = train_target.values