目录
1、格林公式的运用求解曲线积分
一、曲线积分
(1)第一类曲线积分:
求某一条密度不均一的曲线的质量
(2)第二类曲线积分:
求变力沿曲线的做功
(3)格林公式
用处:证明该曲线积分与路径无关 (简化计算)
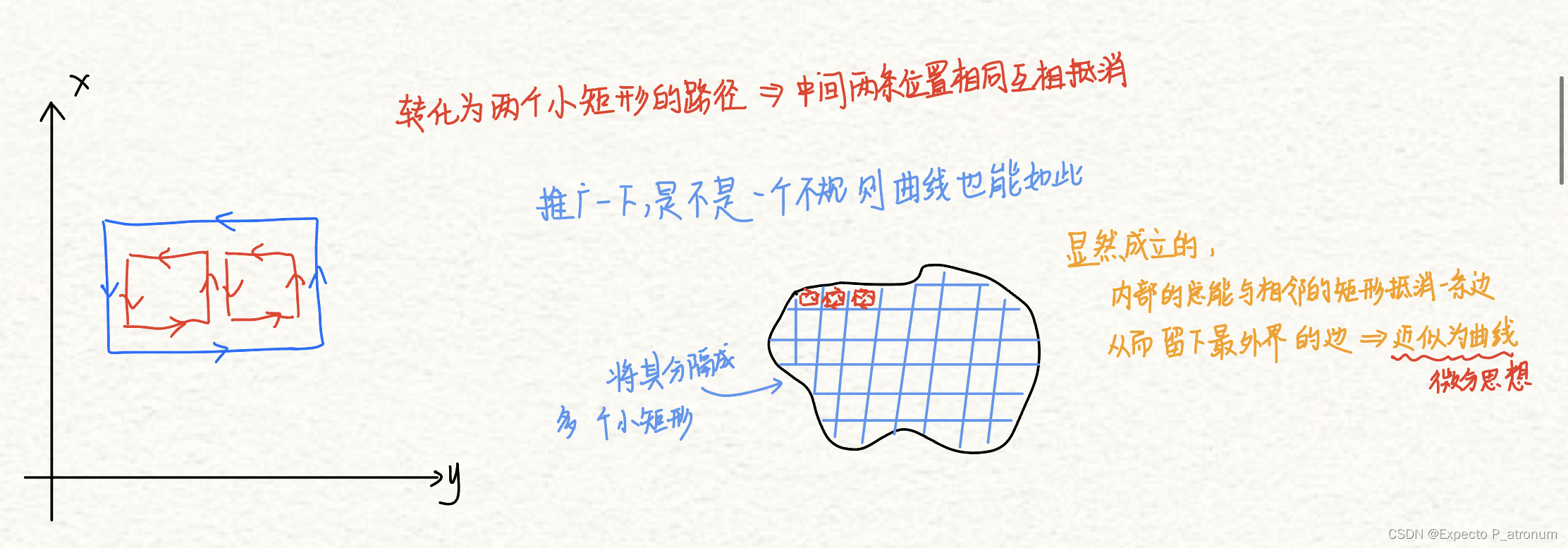
证明过程:
举一个例子,假设一个力将其从点a拉到点b,在从点b拉到了点a,力做了多少功?
做功是0吗?显然不是,当其为变力的时候,功是变化的。所以,在闭合曲线内,如果
,那么此时积分为0,那么此时积分与路径无关,只要起点终点相同,那么积分就不会变化。
那么
和
是怎么来的呢?看如图曲线
那么假设是一个力在这个小矩形内做功,而且上(Fx`)下(Fx)左(Fy`)右(Fy)的力都是不同的,那么力之间有何关系呢?
关系式是这样的,


因为经过微元法之后,任何的曲线都可以看作一条很小对直线,所以其实力与位移的关系可以看作是线性关系的y=kx+b。
那么有关于力的关系式

因为是求功,所以再分别乘上各自的偏移,再同时取二重积分那么就能得出格林公式了。
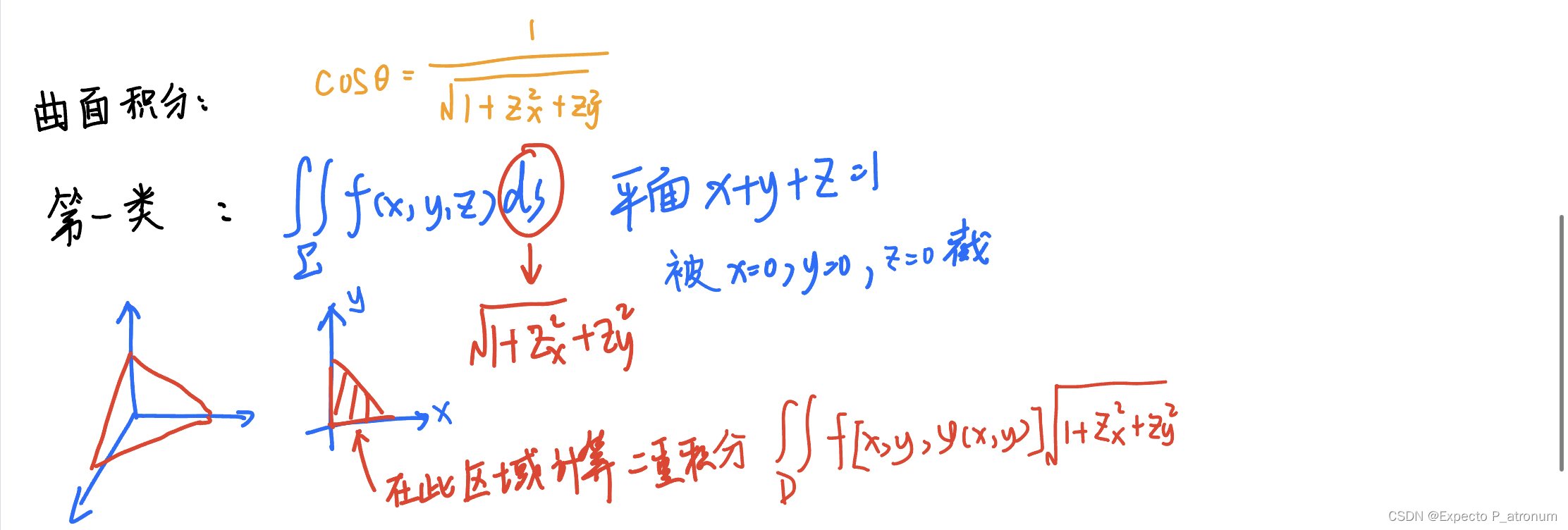
二、曲面积分
(1)第一类曲面积分:
求密度不一样大的曲面的质量
(2)第二类曲面积分:
一个不规则几何体的流量大小
三、考研练习
(1)level 1
1、曲线积分计算
在计算曲线积分时,第一步很关键,一定要观察对称性,对于kxy,kx,ky等这样的式子可以直接删去。
法一、利用代换把y换成x,把ds转化为dx,注意是将斜边化为直角边
法二、将题目中的关系式代入到被积函数中去,可以化繁为简
将
代入式子,可以直接转变被积函数为常数
因为x,y,z是可以对称的,所以
,再利用曲线积分几何意义,求
2、求解路径无关的曲线积分
代入公式
3、曲面积分计算
法一、把z换成f(x,y),同样的dS也要化为dxdy,然后再计算重积分
(2)level 2
1、求力的做功
一个力可以分解为沿着x方向的力Fx和沿着y轴的Fy,所以只要乘上各自的位移在各自相加就能得到做功的大小。所以要先求出F的向量表示,既单位长度✖️角度向量表示
注意:这里的曲线是不闭合的,要使用格林公式必须是闭合曲线!所以在L上多加了一段由(2,0)指向(0,0)的一段,所以在计算时还要再减去这一段。
2、三维的对坐标曲线积分
(3)level 3
1、格林公式的运用求解曲线积分
容易得出来的是Px = Qy(偏导)
但是这道题有一个非常难处理的点就是(x,y)不能等于(0,0),所以不能使用格林公式
所以可以在区域中间取一个圆,并且逆时针,消除(0,0)。但又有问题出现了,环是一个多联通曲线,要内逆外顺才能使用格林公式,那么就再挖去中间的圆,可以转化为求圆环的曲线积分








 本文详细阐述了曲线积分的两类问题,包括第一类曲线积分用于计算密度不均一曲线的质量,第二类曲线积分涉及变力沿曲线的做功。格林公式用于证明某些曲线积分与路径无关并简化计算。此外,文章还讨论了曲面积分的应用,如计算不规则几何体的流量,并提供了不同层次的考研练习题,涵盖从基本的曲线积分计算到更复杂的格林公式应用。
本文详细阐述了曲线积分的两类问题,包括第一类曲线积分用于计算密度不均一曲线的质量,第二类曲线积分涉及变力沿曲线的做功。格林公式用于证明某些曲线积分与路径无关并简化计算。此外,文章还讨论了曲面积分的应用,如计算不规则几何体的流量,并提供了不同层次的考研练习题,涵盖从基本的曲线积分计算到更复杂的格林公式应用。




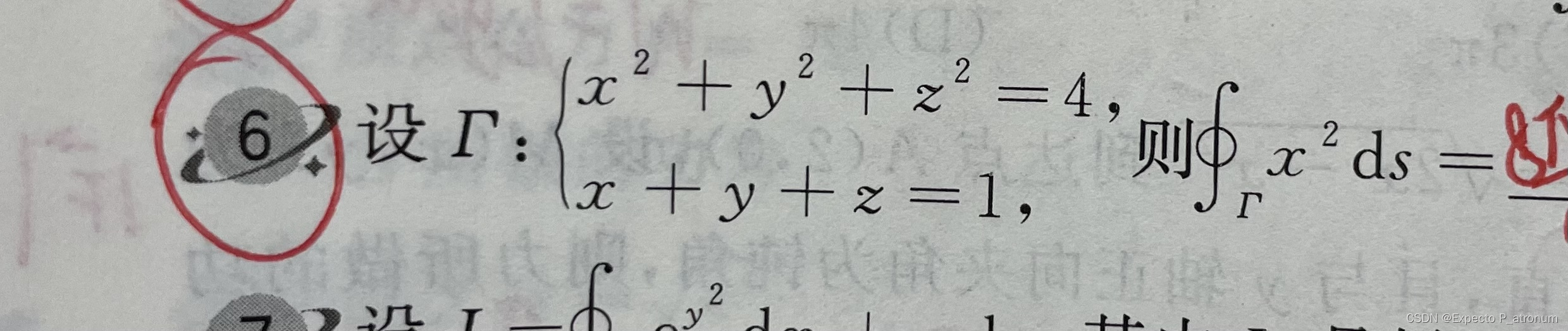
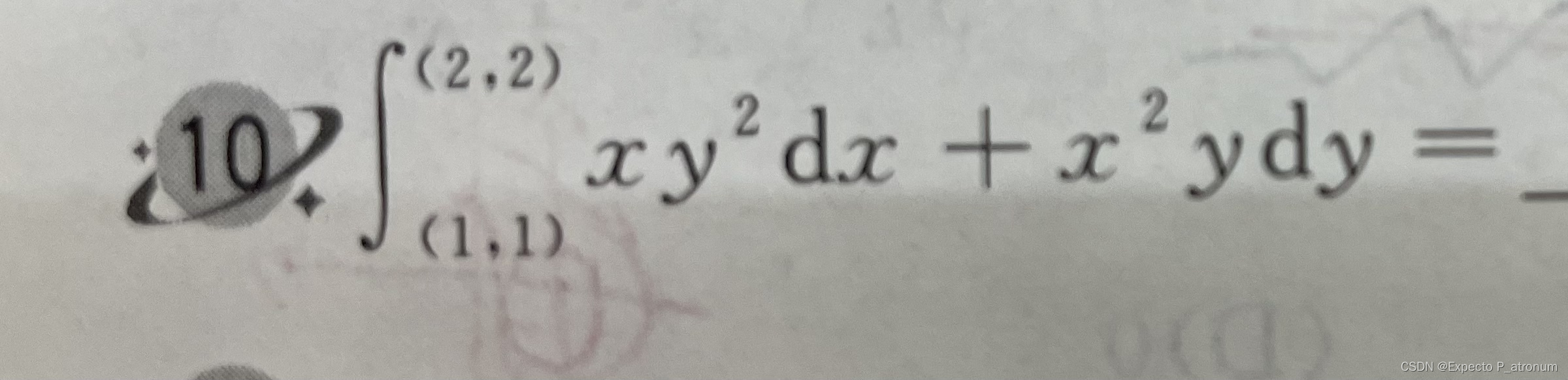



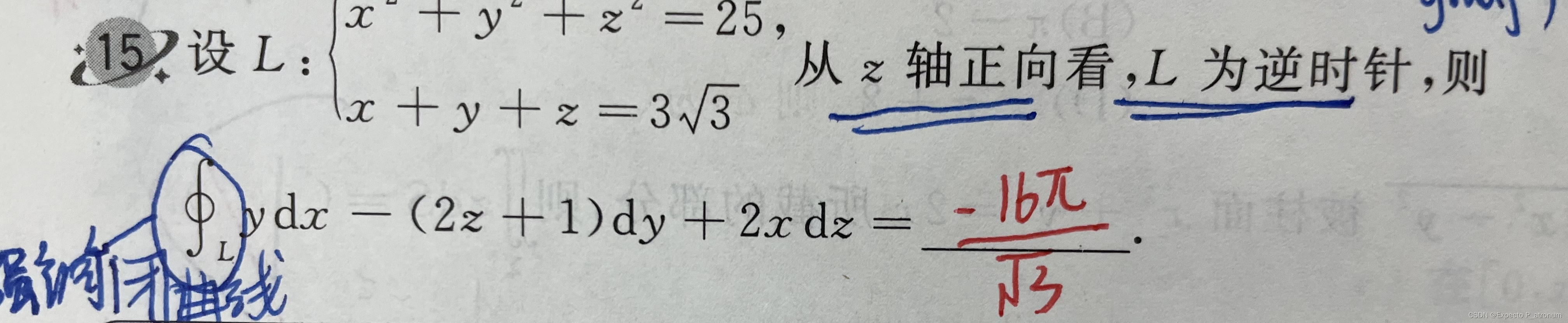
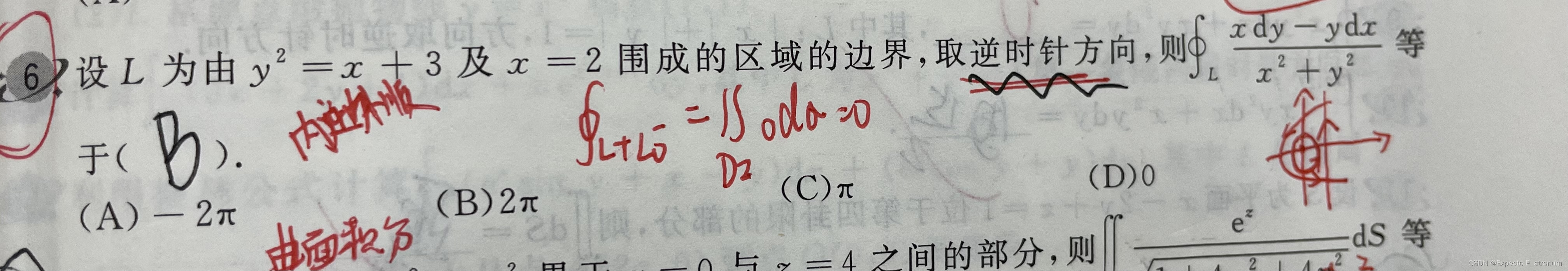
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








