能不能别白嫖啊٩(๑❛ᴗ❛๑)۶
目录
一、前言
1.本人在做建模比赛2020年A题时遇到热传导方程,然后我学习并总结了用有限差分法求解此类偏微分方程(抛物型方程)的解法。
2.本文借鉴《偏微分方程数值解法——孙志忠》,这本书写得浅显易懂。
3.本文不讲复杂的推理过程,只讲方法与结果。
4.相较其他博客而言(绝大多数都是用matlab),我的特点使用Python实现程序的
5.如有问题可在评论区讨论或是私信我
二、问题与定义
1.问题
考虑一维非齐次热传导方程的定解问题

2.定义
对x轴[0,1]区间作m等分,将t轴[0,T]区间作n等分,并记h=1/m,τ=T/n,分别称h和τ为空间步长和时间步长。
记![]() 为网格比。
为网格比。
记 ![]()
网格剖分如下所示
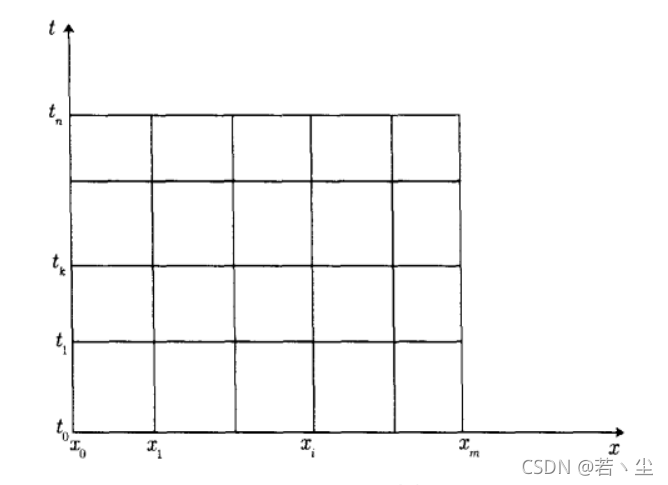
定义网格函数
其中![]()
![]() 是
是![]() 的近似
的近似
三、求解格式
1、向前欧拉格式(古典显格式)
(1)差分格式

可以看出k+1层结点可由第k层得出,因此可以简单循环即可
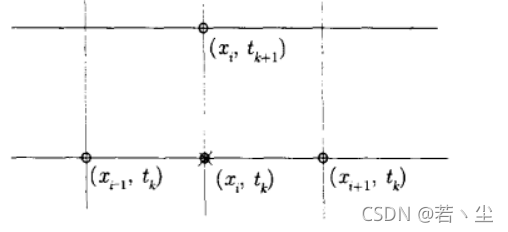
(2)收敛性与稳定性
当r<=1/2时是收敛与稳定的,但是当r>1/2时是不稳定的,也不一定收敛。
2.向后欧拉格式(古典隐格式)
(1)差分格式

可以看出第k层的结点由k+1层结点得出,不能直接迭代求解,必须解方程组
将如上差分格式写为矩阵形式(注意不写的地方为0)

只需要在每一个时间层解这个三对角线性方程组即可,用AX=B代替以上方程组以方便叙述
有两种方法:第一种是直接将方程组两端乘上A逆即可得到X;第二种是用三对角线性方程组的特殊求解方法:追赶法来求解,当矩阵很大的时候速度比求逆矩阵要快得多,方法并不难,我放在最后
(2)收敛性与稳定性
对于任意步长比r必收敛与稳定
3.Crank-Nicolson格式
(1)差分格式

同样是在每一个时间层解一个三对角线性方程组即可
(2)收敛性与稳定性
对于任意步长比r必收敛与稳定
四、追赶法求解三对角线性方程组
五、实例+代码
以下题目的结果均保存至excel中方便观察
1.题目1(《偏微分方程数值解法——孙志忠》书中题目)
时间步长与空间步长均取0.1

代码:
import numpy as np
import pandas as pd
import datetime
start_time = datetime.datetime.now()
np.set_printoptions(suppress=True)
def left_boundary(t): # 左边值
return np.exp(t)
def right_boundary(t): # 右边值
return np.exp(t + 1)
def initial_T(x_max, t_max, delta_x, delta_t, m, n): # 给温度T初始化
T = np.zeros((n + 1, m + 1))
for i in range(m + 1): # 初值
T[0, i] = np.exp(i * delta_x)
for i in range(1, n + 1): # 注意不包括T[0,0]与T[0,-1]
T[i, 0] = left_boundary(i * delta_t) # 左边值
T[i, -1] = right_boundary(i * delta_t) # 右边值
return T
# 一、古典显格式
def one_dimensional_heat_conduction1(T, m, n, r):
# 可以发现当r>=0.5时就发散了
for k in range(1, n + 1): # 时间层
for i in range(1, m): # 空间层
T[k, i] = (1 - 2 * r) * T[k - 1, i] + r * (T[k - 1, i - 1] + T[k - 1, i + 1])
return T.round(6)
# 二、古典隐格式(乘逆矩阵法)
def one_dimensional_heat_conduction2(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + 2 * r) + np.eye(m - 1, k=1) * (-r) + np.eye(m - 1, k=-1) * (-r)
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
T[k, 1:-1] = np.linalg.inv(A) @ F # 左乘A逆
return T.round(6)
# 三、古典隐格式(追赶法)
def one_dimensional_heat_conduction3(T, m, n, r):
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k, 1:-1] = x
return T.round(6)
# 四、Crank-Nicolson(乘逆矩阵法)
def one_dimensional_heat_conduction4(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + r) + np.eye(m - 1, k=1) * (-r * 0.5) + np.eye(m - 1, k=-1) * (-r * 0.5)
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r / 2 * (T[k, 0] + T[k + 1, 0])
F[-1] = r / 2 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
T[k + 1, 1:-1] = np.linalg.inv(A) @ F
return T.round(6)
# 五、Crank-Nicolson(追赶法)
def one_dimensional_heat_conduction5(T, m, n, r):
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
a = np.ones(m - 1) * (-0.5 * r)
a[0] = 0
b = np.ones(m - 1) * (1 + r)
c = np.ones(m - 1) * (-0.5 * r)
c[-1] = 0
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r * 0.5 * (T[k, 0] + T[k + 1, 0])
F[-1] = r * 0.5 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k + 1, 1:-1] = x
return T.round(6)
def exact_solution(T, m, n, r, delta_x, delta_t): # 偏微分方程精确解
for i in range(n + 1):
for j in range(m + 1):
T[i, j] = np.exp(i * delta_t + j * delta_x)
return T.round(6)
a = 1 # 热传导系数
x_max = 1
t_max = 1
delta_x = 0.1 # 空间步长
delta_t = 0.1 # 时间步长
m = int((x_max / delta_x).__round__(4)) # 长度等分成m份
n = int((t_max / delta_t).__round__(4)) # 时间等分成n份
t_grid = np.arange(0, t_max + delta_t, delta_t) # 时间网格
x_grid = np.arange(0, x_max + delta_x, delta_x) # 位置网格
r = (a * delta_t / (delta_x ** 2)).__round__(6) # 网格比
T = initial_T(x_max, t_max, delta_x, delta_t, m, n)
print('长度等分成{}份'.format(m))
print('时间等分成{}份'.format(n))
print('网格比=', r)
p = pd.ExcelWriter('有限差分法-一维热传导-题目1.xlsx')
T1 = one_dimensional_heat_conduction1(T, m, n, r)
T1 = pd.DataFrame(T1, columns=x_grid, index=t_grid) # colums是列号,index是行号
T1.to_excel(p, '古典显格式')
T2 = one_dimensional_heat_conduction2(T, m, n, r)
T2 = pd.DataFrame(T2, columns=x_grid, index=t_grid) # colums是列号,index是行号
T2.to_excel(p, '古典隐格式(乘逆矩阵法)')
T3 = one_dimensional_heat_conduction3(T, m, n, r)
T3 = pd.DataFrame(T3, columns=x_grid, index=t_grid) # colums是列号,index是行号
T3.to_excel(p, '古典隐格式(追赶法)')
T4 = one_dimensional_heat_conduction4(T, m, n, r)
T4 = pd.DataFrame(T4, columns=x_grid, index=t_grid) # colums是列号,index是行号
T4.to_excel(p, 'Crank-Nicolson格式(乘逆矩阵法)')
T5 = one_dimensional_heat_conduction5(T, m, n, r)
T5 = pd.DataFrame(T5, columns=x_grid, index=t_grid) # colums是列号,index是行号
T5.to_excel(p, 'Crank-Nicolson格式(追赶法)')
T6 = exact_solution(T, m, n, r, delta_x, delta_t)
T6 = pd.DataFrame(T6, columns=x_grid, index=t_grid) # colums是列号,index是行号
T6.to_excel(p, '偏微分方程精确解')
p.save()
end_time = datetime.datetime.now()
print('运行时间为', (end_time - start_time))
书中Crank-Nicolson的数值解
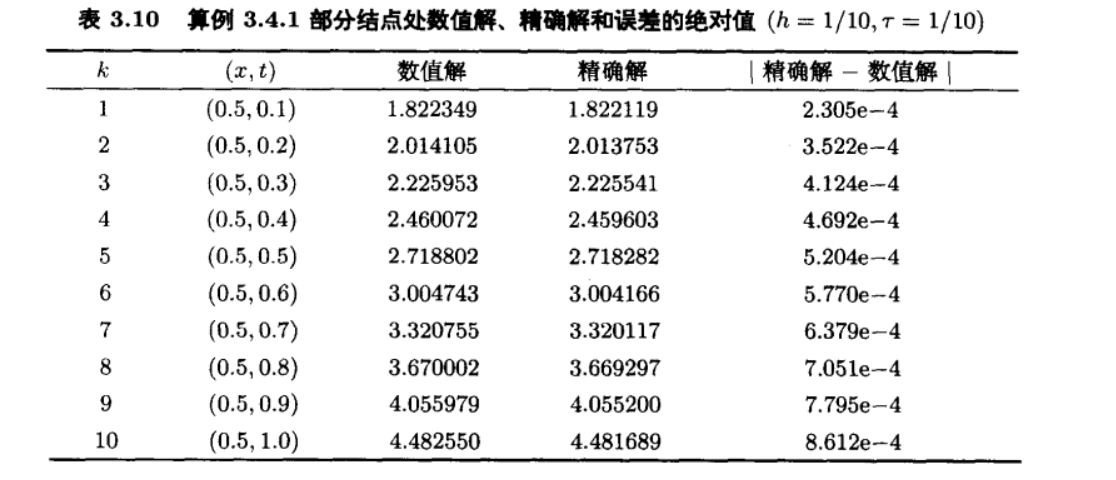
可以看出与我的程序答案完全一致。
其余格式的结果与我的程序答案都是一样的。
结果分析大家就自己做了,我就不赘述了。
2.题目2

(1)理论分析
由生活实际知,温度不会无限制增大,当时间趋于一定的值时,温度将会稳定。
而由一维热传导方程知,
温度与距离将会呈线性关系,若以杆最左端为x=0则有:y=175+4x(x=5时y=195)

在这个题目中,f(x,t)=0,差分格式用矩阵比较容易表达与求解

如果f(x,t)≠0,那么可以自己在程序中修改矩阵的值
(2)代码
import numpy as np
import pandas as pd
import datetime
start_time = datetime.datetime.now()
np.set_printoptions(suppress=True)
def left_boundary(t): # 左边值
T = 25 + 15 * t
if T < 175:
return T
else:
return 175
def right_boundary(t): # 右边值
T = 25 + 17 * t
if T < 195:
return T
else:
return 195
def initial_T(x_max, t_max, delta_x, delta_t, m, n): # 给温度T初始化
T = np.zeros((n + 1, m + 1))
for i in range(m + 1): # 初值
T[0, i] = 25
for i in range(1, n + 1): # 注意不包括T[0,0]与T[0,-1]
T[i, 0] = left_boundary(i * delta_t) # 左边值
T[i, -1] = right_boundary(i * delta_t) # 右边值
return T
# 一、古典显格式
def one_dimensional_heat_conduction1(T, m, n, r):
# 可以发现当r>=0.5时就发散了
for k in range(1, n + 1): # 时间层
for i in range(1, m): # 空间层
T[k, i] = (1 - 2 * r) * T[k - 1, i] + r * (T[k - 1, i - 1] + T[k - 1, i + 1])
return T.round(6)
# 二、古典隐格式(乘逆矩阵法)
def one_dimensional_heat_conduction2(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + 2 * r) + np.eye(m - 1, k=1) * (-r) + np.eye(m - 1, k=-1) * (-r)
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
T[k, 1:-1] = np.linalg.inv(A) @ F # 左乘A逆
return T.round(6)
# 三、古典隐格式(追赶法)
def one_dimensional_heat_conduction3(T, m, n, r):
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k, 1:-1] = x
return T.round(6)
# 四、Crank-Nicolson(乘逆矩阵法)
def one_dimensional_heat_conduction4(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + r) + np.eye(m - 1, k=1) * (-r * 0.5) + np.eye(m - 1, k=-1) * (-r * 0.5)
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r / 2 * (T[k, 0] + T[k + 1, 0])
F[-1] = r / 2 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
T[k + 1, 1:-1] = np.linalg.inv(A) @ F
return T.round(6)
# 五、Crank-Nicolson(追赶法)
def one_dimensional_heat_conduction5(T, m, n, r):
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
a = np.ones(m - 1) * (-0.5 * r)
a[0] = 0
b = np.ones(m - 1) * (1 + r)
c = np.ones(m - 1) * (-0.5 * r)
c[-1] = 0
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r * 0.5 * (T[k, 0] + T[k + 1, 0])
F[-1] = r * 0.5 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k + 1, 1:-1] = x
return T.round(6)
a = 0.5 # 热传导系数
x_max = 5
t_max = 100
delta_x = 0.1 # 空间步长
delta_t = 0.1 # 时间步长
m = int((x_max / delta_x).__round__(4)) # 长度等分成m份
n = int((t_max / delta_t).__round__(4)) # 时间等分成n份
t_grid = np.arange(0, t_max + delta_t, delta_t) # 时间网格
x_grid = np.arange(0, x_max + delta_x, delta_x) # 位置网格
r = (a * delta_t / (delta_x ** 2)).__round__(6) # 网格比
T = initial_T(x_max, t_max, delta_x, delta_t, m, n)
print('长度等分成{}份'.format(m))
print('时间等分成{}份'.format(n))
print('网格比=', r)
p = pd.ExcelWriter('有限差分法-一维热传导-题目2.xlsx')
T1 = one_dimensional_heat_conduction1(T, m, n, r)
T1 = pd.DataFrame(T1, columns=x_grid, index=t_grid) # colums是列号,index是行号
T1.to_excel(p, '古典显格式')
T2 = one_dimensional_heat_conduction2(T, m, n, r)
T2 = pd.DataFrame(T2, columns=x_grid, index=t_grid) # colums是列号,index是行号
T2.to_excel(p, '古典隐格式(乘逆矩阵法)')
T3 = one_dimensional_heat_conduction3(T, m, n, r)
T3 = pd.DataFrame(T3, columns=x_grid, index=t_grid) # colums是列号,index是行号
T3.to_excel(p, '古典隐格式(追赶法)')
T4 = one_dimensional_heat_conduction4(T, m, n, r)
T4 = pd.DataFrame(T4, columns=x_grid, index=t_grid) # colums是列号,index是行号
T4.to_excel(p, 'Crank-Nicolson格式(乘逆矩阵法)')
T5 = one_dimensional_heat_conduction5(T, m, n, r)
T5 = pd.DataFrame(T5, columns=x_grid, index=t_grid) # colums是列号,index是行号
T5.to_excel(p, 'Crank-Nicolson格式(追赶法)')
p.save()
end_time = datetime.datetime.now()
print('运行时间为', (end_time - start_time))
(3)运行结果与分析
长度等分成50份
时间等分成1000份
网格比= 5.0
C:/Users/86189/Desktop/Technology/Python_File/数学建模/自己总结/有限差分法-一维热传导-题目1.py:43: RuntimeWarning: overflow encountered in double_scalars
T[k, i] = (1 - 2 * r) * T[k - 1, i] + r * (T[k - 1, i - 1] + T[k - 1, i + 1])
C:/Users/86189/Desktop/Technology/Python_File/数学建模/自己总结/有限差分法-一维热传导-题目1.py:44: RuntimeWarning: overflow encountered in multiply
return T.round(6)
运行时间为 0:00:06.094756
可以发现显格式已经不收敛了,其余格式都收敛;
最终的温度都稳定为y=175+4x,符合理论分析。
3.特殊的例子:题目3

这里仅仅是修改了边值条件,但是情况却大有不同了!
(1)代码
注:结果会存到“有限差分法-一维热传导.xlsx”中,方便大家观察
import numpy as np
import pandas as pd
import datetime
start_time = datetime.datetime.now()
np.set_printoptions(suppress=True)
def left_boundary(t): # 左边
return 175
def right_boundary(t): # 右边值
return 195
def initial_T(x_max, t_max, delta_x, delta_t, m, n): # 给温度T初始化
T = np.zeros((n + 1, m + 1))
for i in range(m + 1): # 初值
T[0, i] = 25
for i in range(1, n + 1): # 注意不包括T[0,0]与T[0,-1]
T[i, 0] = left_boundary(i * delta_t) # 左边值
T[i, -1] = right_boundary(i * delta_t) # 右边值
return T
# 一、古典显格式
def one_dimensional_heat_conduction1(T, m, n, r):
# 可以发现当r>=0.5时就发散了
for k in range(1, n + 1): # 时间层
for i in range(1, m): # 空间层
T[k, i] = (1 - 2 * r) * T[k - 1, i] + r * (T[k - 1, i - 1] + T[k - 1, i + 1])
return T.round(6)
# 二、古典隐格式(乘逆矩阵法)
def one_dimensional_heat_conduction2(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + 2 * r) + np.eye(m - 1, k=1) * (-r) + np.eye(m - 1, k=-1) * (-r)
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
T[k, 1:-1] = np.linalg.inv(A) @ F # 左乘A逆
return T.round(6)
# 三、古典隐格式(追赶法)
def one_dimensional_heat_conduction3(T, m, n, r):
a = np.ones(m - 1) * (-r)
a[0] = 0
b = np.ones(m - 1) * (1 + 2 * r)
c = np.ones(m - 1) * (-r)
c[-1] = 0
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
for k in range(1, n + 1): # 时间层range(1, n + 1)
F[0] = T[k - 1, 1] + r * T[k, 0]
F[-1] = T[k - 1, m - 1] + r * T[k, m]
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 2): # 空间层
F[i] = T[k - 1, i + 1] # 给F赋值
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k, 1:-1] = x
return T.round(6)
# 四、Crank-Nicolson(乘逆矩阵法)
def one_dimensional_heat_conduction4(T, m, n, r):
A = np.eye(m - 1, k=0) * (1 + r) + np.eye(m - 1, k=1) * (-r * 0.5) + np.eye(m - 1, k=-1) * (-r * 0.5)
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r / 2 * (T[k, 0] + T[k + 1, 0])
F[-1] = r / 2 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
T[k + 1, 1:-1] = np.linalg.inv(A) @ F
return T.round(6)
# 五、Crank-Nicolson(追赶法)
def one_dimensional_heat_conduction5(T, m, n, r):
C = np.eye(m - 1, k=0) * (1 - r) + np.eye(m - 1, k=1) * (0.5 * r) + np.eye(m - 1, k=-1) * (0.5 * r)
a = np.ones(m - 1) * (-0.5 * r)
a[0] = 0
b = np.ones(m - 1) * (1 + r)
c = np.ones(m - 1) * (-0.5 * r)
c[-1] = 0
for k in range(0, n): # 时间层
F = np.zeros(m - 1) # m-1个元素,索引0~(m-2)
F[0] = r * 0.5 * (T[k, 0] + T[k + 1, 0])
F[-1] = r * 0.5 * (T[k, m] + T[k + 1, m])
F = C @ T[k, 1:m] + F
y = np.zeros(m - 1)
beta = np.zeros(m - 1)
x = np.zeros(m - 1)
y[0] = F[0] / b[0]
d = b[0]
for i in range(1, m - 1):
beta[i - 1] = c[i - 1] / d
d = b[i] - a[i] * beta[i - 1]
y[i] = (F[i] - a[i] * y[i - 1]) / d
x[-1] = y[-1]
for i in range(m - 3, -1, -1):
x[i] = y[i] - beta[i] * x[i + 1]
T[k + 1, 1:-1] = x
return T.round(6)
a = 0.5 # 热传导系数
x_max = 5
t_max = 100
delta_x = 0.1 # 空间步长
delta_t = 0.1 # 时间步长
m = int((x_max / delta_x).__round__(4)) # 长度等分成m份
n = int((t_max / delta_t).__round__(4)) # 时间等分成n份
t_grid = np.arange(0, t_max + delta_t, delta_t) # 时间网格
x_grid = np.arange(0, x_max + delta_x, delta_x) # 位置网格
r = (a * delta_t / (delta_x ** 2)).__round__(6) # 网格比
T = initial_T(x_max, t_max, delta_x, delta_t, m, n)
print('长度等分成{}份'.format(m))
print('时间等分成{}份'.format(n))
print('网格比=', r)
p = pd.ExcelWriter('有限差分法-一维热传导-题目3.xlsx')
T1 = one_dimensional_heat_conduction1(T, m, n, r)
T1 = pd.DataFrame(T1, columns=x_grid, index=t_grid) # colums是列号,index是行号
T1.to_excel(p, '古典显格式')
T2 = one_dimensional_heat_conduction2(T, m, n, r)
T2 = pd.DataFrame(T2, columns=x_grid, index=t_grid) # colums是列号,index是行号
T2.to_excel(p, '古典隐格式(乘逆矩阵法)')
T3 = one_dimensional_heat_conduction3(T, m, n, r)
T3 = pd.DataFrame(T3, columns=x_grid, index=t_grid) # colums是列号,index是行号
T3.to_excel(p, '古典隐格式(追赶法)')
T4 = one_dimensional_heat_conduction4(T, m, n, r)
T4 = pd.DataFrame(T4, columns=x_grid, index=t_grid) # colums是列号,index是行号
T4.to_excel(p, 'Crank-Nicolson格式(乘逆矩阵法)')
T5 = one_dimensional_heat_conduction5(T, m, n, r)
T5 = pd.DataFrame(T5, columns=x_grid, index=t_grid) # colums是列号,index是行号
T5.to_excel(p, 'Crank-Nicolson格式(追赶法)')
p.save()
end_time = datetime.datetime.now()
print('运行时间为', (end_time - start_time))
(2)运行结果与分析
长度等分成50份
时间等分成1000份
网格比= 5.0
C:/Users/86189/Desktop/Technology/Python_File/数学建模/自己总结/有限差分法-一维热传导-题目3.py:35: RuntimeWarning: overflow encountered in double_scalars
T[k, i] = (1 - 2 * r) * T[k - 1, i] + r * (T[k - 1, i - 1] + T[k - 1, i + 1])
C:/Users/86189/Desktop/Technology/Python_File/数学建模/自己总结/有限差分法-一维热传导-题目3.py:36: RuntimeWarning: overflow encountered in multiply
return T.round(6)
运行时间为 0:00:05.578520
显格式仍不收敛。
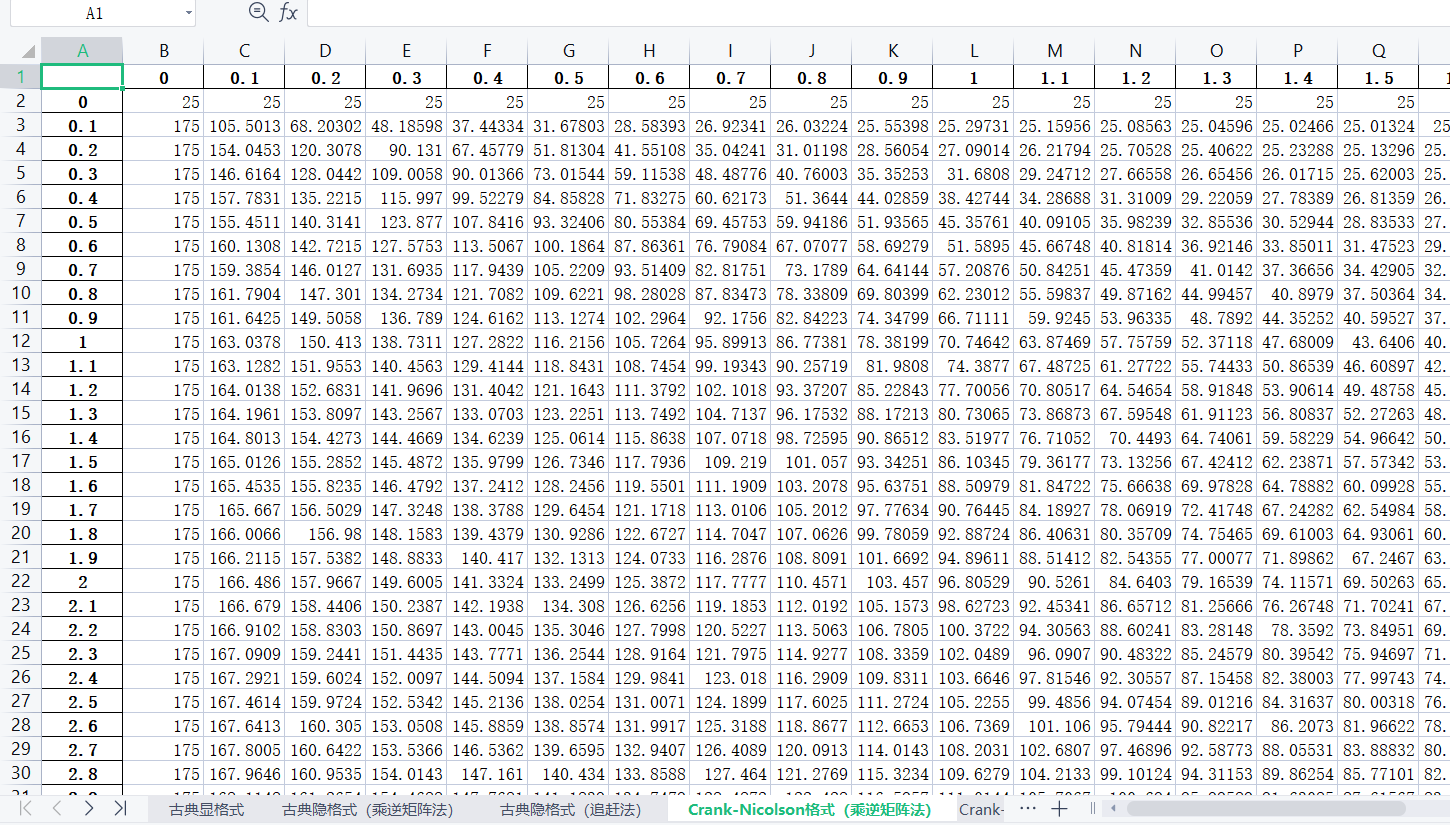
注意!Crank-Nicolson格式虽然最终收敛于y=175+4x,但是可以发现在最初的1秒内出现了数值伪振荡,这是因为我们给定的边值不合理导致的。通俗的讲,试想在生活实际中那能让一根杆在极短时间从25摄氏度跃变至175摄氏度,这合理吗?并不合理,这么大的变化率导致CN格式出现了数值伪振荡。并且只有当网格比稍大的时候才会出现这种情况,网格比小时仍然可用CN格式
























 2081
2081











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










