人工智能十大基础算法

目录

1.线性回归

2.逻辑回归

3.决策树

4.朴素贝叶斯

5.支持向量机

6.K- 最近邻算法（KNN） 

7.K- 均值

8.随机森林 

9.降维

10.人工神经网络（ANN）

---

 事实上，人工智能已经存在于我们生活中很久了。但对很多人来讲，人工智能还是一个较为“高深”的技术，然而再高深的技术，也是从基础原理开始的。人工智能领域中就流传着10大算法，它们的原理浅显，很早就被发现、应用，甚至你在中学时就学过，在生活中也都极为常见。

1.线性回归

线性回归（Linear Regression）可能是最流行的机器学习算法。线性回归就是要找一条直线，并且让这条直线尽可能地拟合散点图中的数据点。它试图通过将直线方程与该数据拟合来表示自变量（x 值）和数值结果（y 值）。然后就可以用这条线来预测未来的值！

这种算法最常用的技术是最小二乘法（Least of squares）。这个方法计算出最佳拟合线，以使得与直线上每个数据点的垂直距离最小。总距离是所有数据点的垂直距离（绿线）的平方和。其思想是通过最小化这个平方误差或距离来拟合模型。

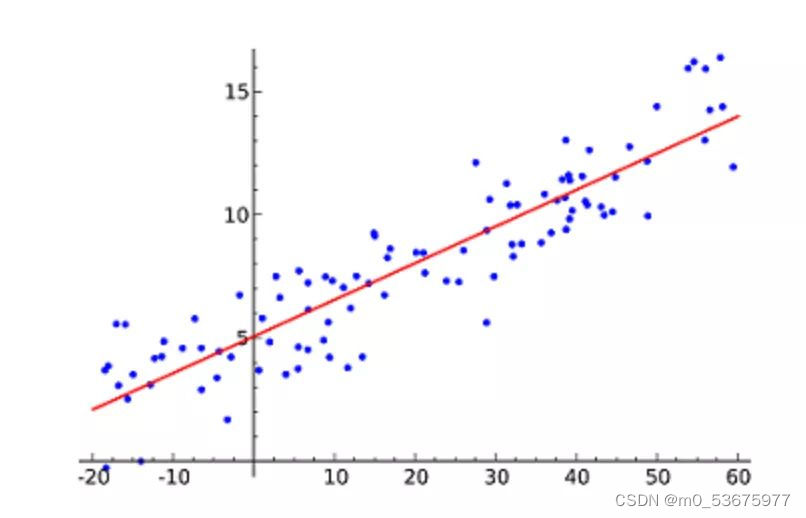
例如，简单线性回归，它有一个自变量（x 轴）和一个因变量（y 轴）

比如预测明年的房价涨幅、下一季度新产品的销量等等。听起来并不难，不过线性回归算法的难点并不在于得出预测值，而在于如何更精确。为了那个可能十分细微的数字，多少工程师为之耗尽了青春和头发。

2.逻辑回归

逻辑回归（Logistic regression）与线性回归类似，但逻辑回归的结果只能有两个的值。如果说线性回归是在预测一个开放的数值，那逻辑回归更像是做一道是或不是的判断题。

逻辑函数中Y值的范围从 0 到 1，是一个概率值。逻辑函数通常呈S 型，曲线把图表分成两块区域，因此适合用于分类任务。

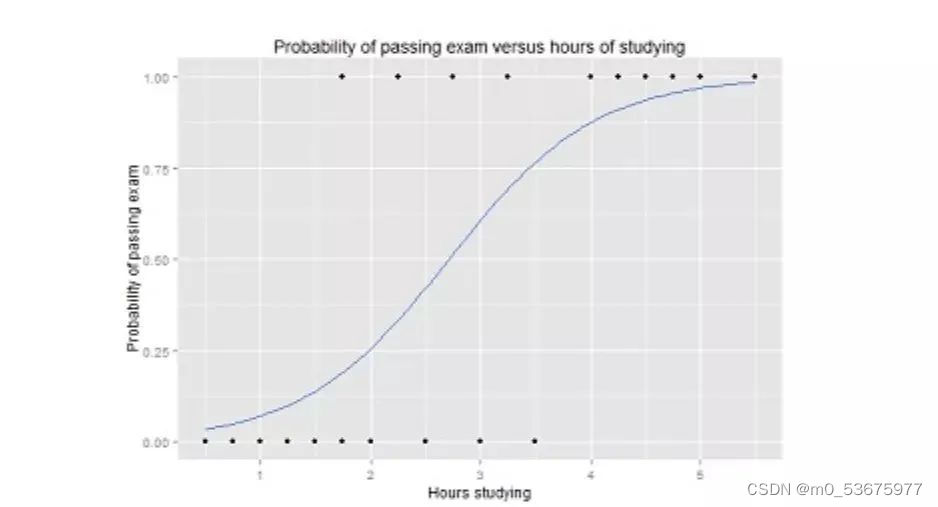
比如上面的逻辑回归曲线图，显示了通过考试的概率与学习时间的关系，可以用来预测是否可以通过考试。

逻辑回归经常被电商或者外卖平台用来预测用户对品类的购买偏好。

3.决策树

如果说线性和逻辑回归都是把任务在一个回合内结束，那么决策树（Decision Trees）就是一个多步走的动作，它同样用于回归和分类任务中，不过场景通常更复杂且具体。

举个简单例子，老师面对一个班级的学生，哪些是好学生？如果简单判断考试90分就算好学生好像太粗暴了，不能唯分数论。那面对成绩不到90分的学生，我们可以从作业、出勤、提问等几个方面分开讨论。

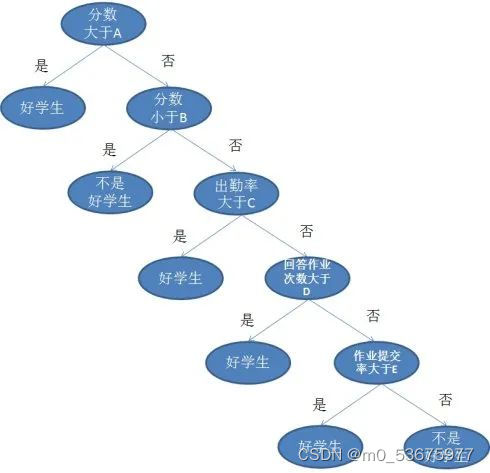
以上就是一个决策树的图例，其中每一个有分叉的圈称为节点。在每个节点上，我们根据可用的特征询问有关数据的问题。左右分支代表可能的答案。最终节点（即叶节点）对应于一个预测值。

每个特征的重要性是通过自顶向下方法确定的。节点越高，其属性就越重要。比如在上面例子中的老师就认为出勤率比做作业重要，所以出勤率的节点就更高，当然分数的节点更高。

4.朴素贝叶斯

朴素贝叶斯（Naive Bayes）是基于贝叶斯定理，即两个条件关系之间。它测量每个类的概率，每个类的条件概率给出 x 的值。这个算法用于分类问题，得到一个二进制“是 / 非”的结果。看看下面的方程式。

朴素贝叶斯分类器是一种流行的统计技术，经典应用是过滤垃圾邮件。

当然，学堂君赌一顿火锅，80%的人没看懂上面这段话。（80%这个数字是猜的，但经验直觉就是一种贝叶斯式的计算。）

用非术语解释贝叶斯定理，就是通过A条件下发生B的概率，去得出B条件下发生A的概率。比如说，小猫喜欢你，有a%可能性在你面前翻肚皮，请问小猫在你面前翻肚皮，有多少概率喜欢你？

当然，这样做题，等于抓瞎，所以我们还需要引入其他数据，比如小猫喜欢你，有b%可能和你贴贴，有c%概率发出呼噜声。所以我们如何知道小猫有多大概率喜欢自己呢，通过贝叶斯定理就可以从翻肚皮，贴贴和呼噜的概率中计算出来。

5.支持向量机

支持向量机（Support Vector Machine，SVM）是一种用于分类问题的监督算法。支持向量机试图在数据点之间绘制两条线，它们之间的边距最大。为此，我们将数据项绘制为 n 维空间中的点，其中，n 是输入特征的数量。在此基础上，支持向量机找到一个最优边界，称为超平面（Hyperplane），它通过类标签将可能的输出进行最佳分离。

超平面与最近的类点之间的距离称为边距。最优超平面具有最大的边界，可以对点进行分类，从而使最近的数据点与这两个类之间的距离最大化。

所以支持向量机想要解决的问题也就是如何把一堆数据做出区隔，它的主要应用场景有字符识别、面部识别、文本分类等各种识别。

6.K- 最近邻算法（KNN） 

K- 最近邻算法（K-Nearest Neighbors，KNN）非常简单。KNN 通过在整个训练集中搜索 K 个最相似的实例，即 K 个邻居，并为所有这些 K 个实例分配一个公共输出变量，来对对象进行分类。

K 的选择很关键：较小的值可能会得到大量的噪声和不准确的结果，而较大的值是不可行的。它最常用于分类，但也适用于回归问题。

用于评估实例之间相似性的距离可以是欧几里得距离（Euclidean distance）、曼哈顿距离（Manhattan distance）或明氏距离（Minkowski distance）。欧几里得距离是两点之间的普通直线距离。它实际上是点坐标之差平方和的平方根。

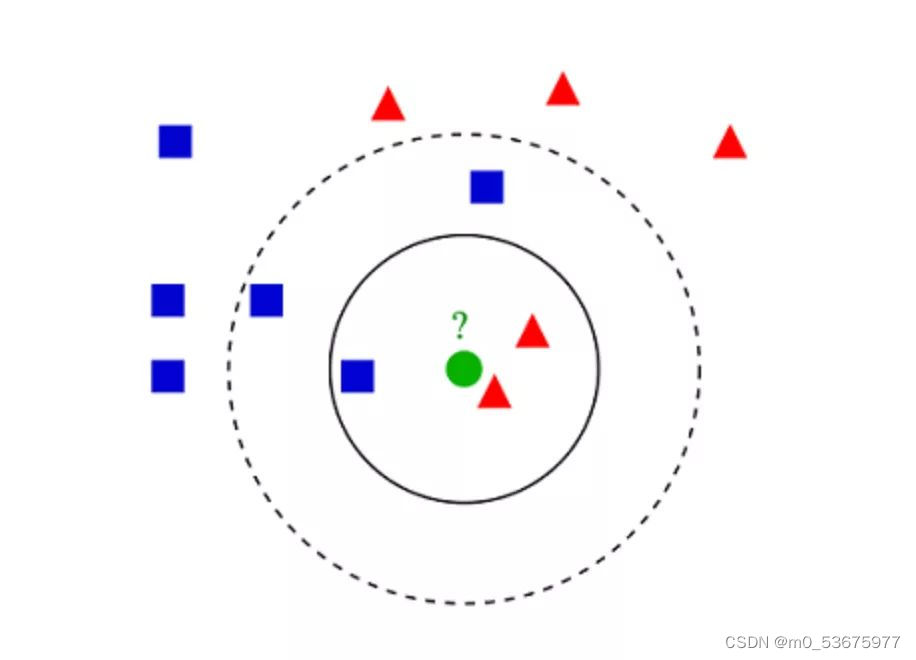
 KNN理论简单，容易实现，可用于文本分类、模式识别、聚类分析等。

7.K- 均值

K- 均值（K-means）是通过对数据集进行分类来聚类的。例如，这个算法可用于根据购买历史将用户分组。它在数据集中找到 K 个聚类。K- 均值用于无监督学习，因此，我们只需使用训练数据 X，以及我们想要识别的聚类数量 K。

该算法根据每个数据点的特征，将每个数据点迭代地分配给 K 个组中的一个组。它为每个 K- 聚类（称为质心）选择 K 个点。基于相似度，将新的数据点添加到具有最近质心的聚类中。这个过程一直持续到质心停止变化为止。

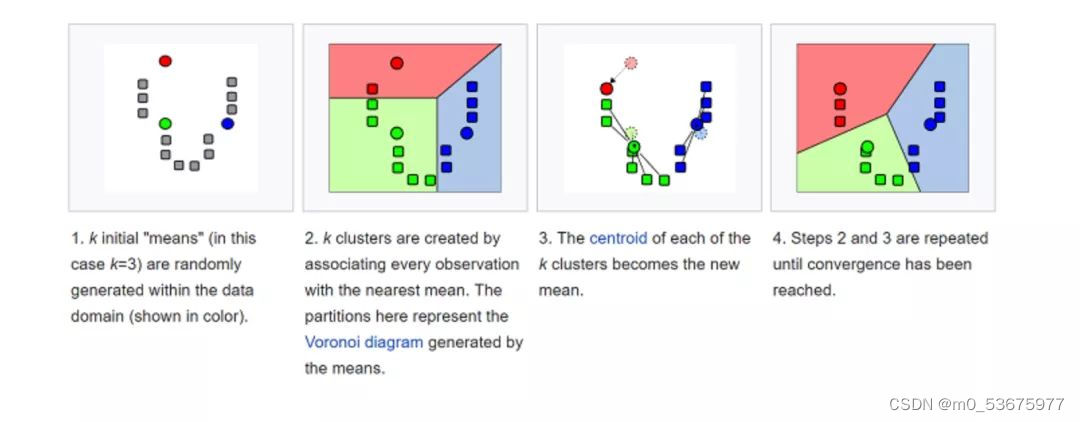
生活中，K- 均值在欺诈检测中扮演了重要角色，在汽车、医疗保险和保险欺诈检测领域中广泛应用。

8.随机森林 

随机森林（Random Forest）是一种非常流行的集成机器学习算法。这个算法的基本思想是，许多人的意见要比个人的意见更准确。在随机森林中，我们使用决策树集成（参见决策树）。

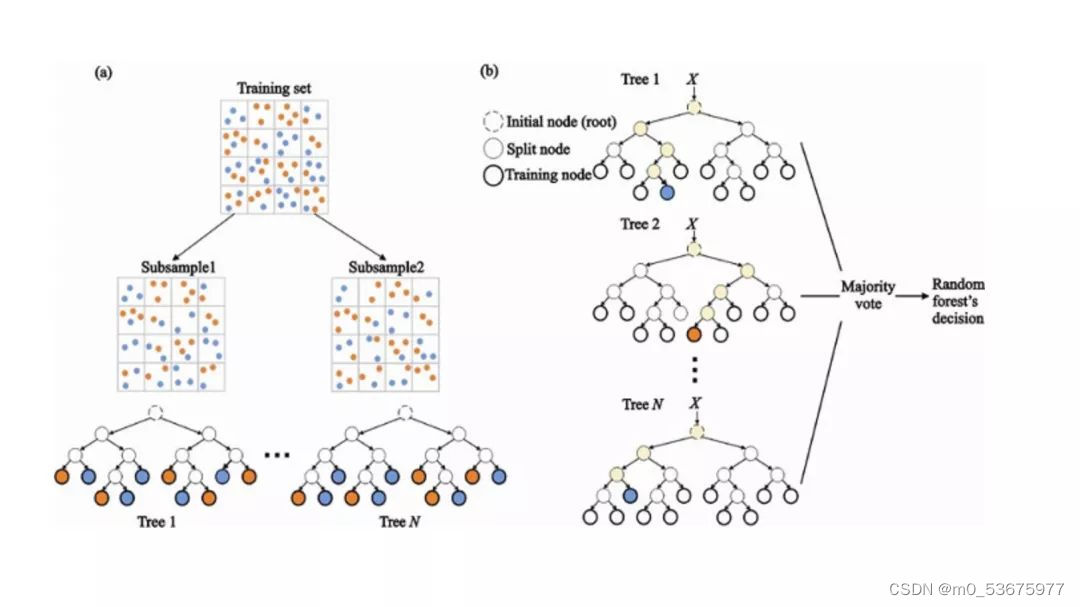
（a）在训练过程中，每个决策树都是基于训练集的引导样本来构建的。

（b）在分类过程中，输入实例的决定是根据多数投票做出的。

随机森林拥有广泛的应用前景，从市场营销到医疗保健保险，既可以用来做市场营销模拟的建模，统计客户来源、保留及流失，也可以用来预测疾病的风险和病患者的易感性。

9.降维

由于我们今天能够捕获的数据量之大，机器学习问题变得更加复杂。这就意味着训练极其缓慢，而且很难找到一个好的解决方案。这一问题，通常被称为“维数灾难”（Curse of dimensionality）。

降维（Dimensionality reduction）试图在不丢失最重要信息的情况下，通过将特定的特征组合成更高层次的特征来解决这个问题。主成分分析（Principal Component Analysis，PCA）是最流行的降维技术。

主成分分析通过将数据集压缩到低维线或超平面 / 子空间来降低数据集的维数。这尽可能地保留了原始数据的显著特征。

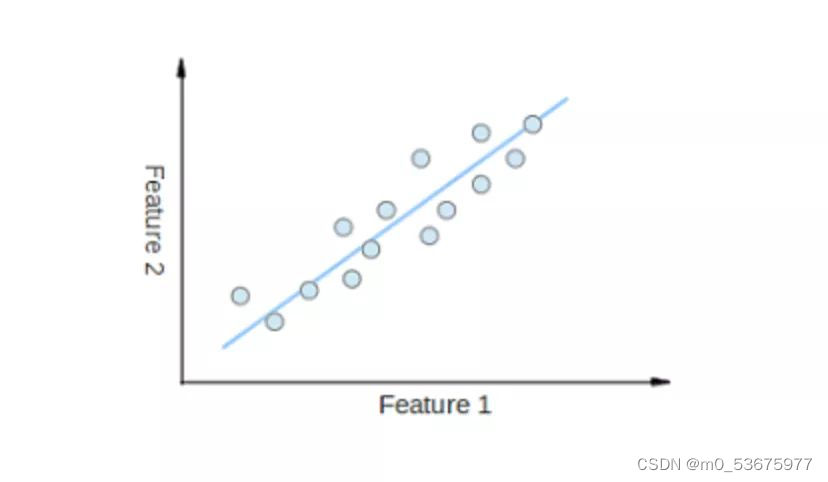
 可以通过将所有数据点近似到一条直线来实现降维的示例。

10.人工神经网络（ANN）

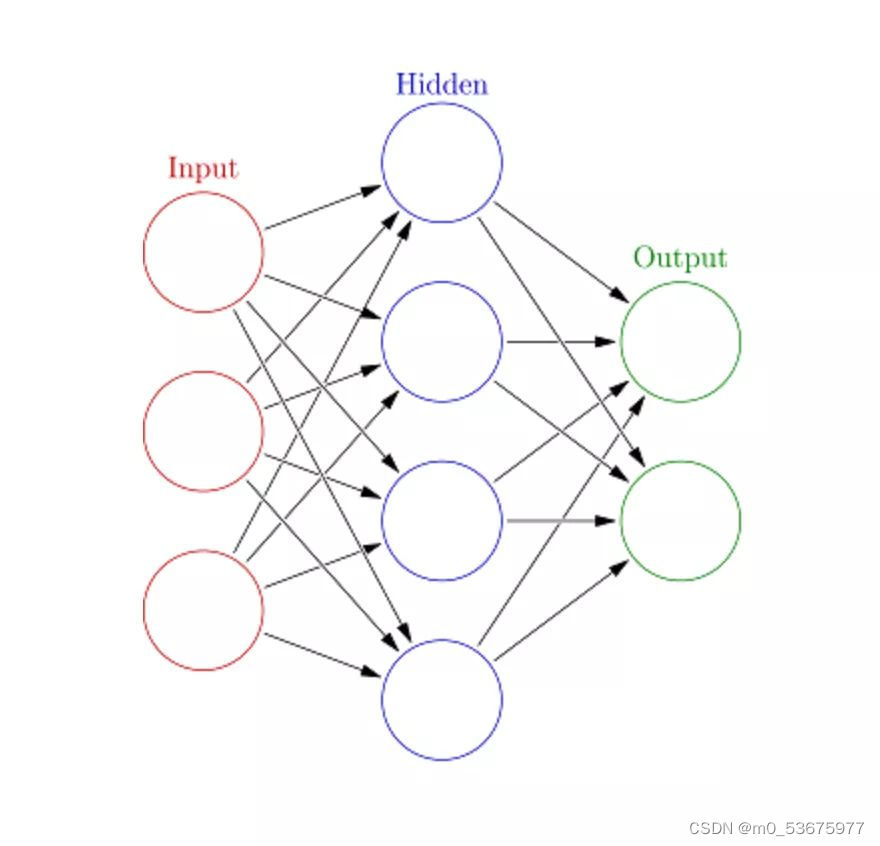
人工神经网络（Artificial Neural Networks，ANN）可以处理大型复杂的机器学习任务。神经网络本质上是一组带有权值的边和节点组成的相互连接的层，称为神经元。在输入层和输出层之间，我们可以插入多个隐藏层。人工神经网络使用了两个隐藏层。除此之外，还需要处理深度学习。

人工神经网络的工作原理与大脑的结构类似。一组神经元被赋予一个随机权重，以确定神经元如何处理输入数据。通过对输入数据训练神经网络来学习输入和输出之间的关系。在训练阶段，系统可以访问正确的答案。

如果网络不能准确识别输入，系统就会调整权重。经过充分的训练后，它将始终如一地识别出正确的模式。