衍射的角谱理论

一、单色平面波与本征函数

不考虑夫琅禾费近似, 则相干光场在给定二平面间的传播过程就是通过一个二维线性空不变系统。

        上式函数是这个系统的本征函数，表示振幅为1的平面波在xy平面上的复振幅分布，空间频率分量 = cos / ,   = cos / 与平面波的传播方向相联系, 空间频率表示了单色平面波的传播方向。

        这说明, 相干光场在自由空间给定两平面间的传播过程相当于通过一个线性空不变系统，单色平面波复振幅分布即为该系统的本征函数。

在z = 0平面上的复振幅分布为

 在z = 平面上的复振幅分布为

        可见，单色平面波从z = 0平面传播到z = 平面上，其在x-y平面上的相位分布不变，只是整体发生了一个相移。

相当于乘上一个复常数，这正好是本征函数的定义，而 

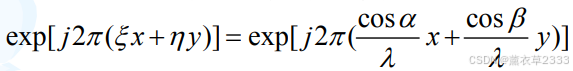
正好是线性平移不变系统的本征函数。

         一定空间频率对应着一定的空间传播方向, 不同空间频率对应着不同的空间传播方向。

        用传播角度表示空间频谱——角谱。

二、角谱的传播

 推导可得

 该式给出了两个平行平面之间的角谱传播规律。

        此式表明，知道了z=0 平面上角谱后，利用上式可求出观察面上的角谱，然后通过傅里叶逆变换求出观察面上的复振幅分布。

现讨论上式：

（1）当 +  < 1时，

是实数，则对于某一确定的（，），该式表示沿空间某一确定方向传播的平面波。当（，）取不同值时，该式表示光场中各个角谱分量的传播情况。该式说明，经过z 距离的传播，光场中各个平面波的振幅不发生变化，只是改变了各自的相对相位。

（2）当 +  > 1时，

         随z的增大，迅速衰减，在几个波长的距离内几乎衰减为0，对应于这些传播方向的波动分量称为倏逝波，通常情况下略去不计。

（3）当 +  = 1时，cos = 0

        该波动分量的传播方向垂直于z轴, 它在z轴方向的净能流为0，对角谱传播无贡献。

可以改写为：

和A分别看成线性不变系统的输入和输出频谱，传递函数为：

        它表明，系统的传递函数相当于一个低通滤波器，具有有限带宽，其截止频率为1/。在频率平面上，这个滤波器相当于半径为1/的圆孔区域。 

        频率小于1/，模为1，对各种频率成分的振幅无影响，但是要引入与频率有关的相移，频率大于1/，被截止。

        这说明，光波衍射传播过程是一个低通滤波的过程。

        从空域种看，比波长还小的精细结构信息，或是空间频率高于1/的信息，在波长为的单色照明下不能沿z方向向前传播。此即衍射的角谱理论。如果把描述球面子波相干叠加的基尔霍夫理论称为衍射的球面波理论，角谱理论则是衍射的平面波理论。它描述孔径平面上不同传播方向的平面波分量在传播距离z后，各自引入与频率有关的相移，然后再线性叠加，产生观察平面上的场分布。

三、孔径对角谱的影响

3.1 衍射屏及其复振幅透过率（反射率）

衍射屏：只要能以某种方式对入射光波的波面进行调制(包括振幅调制，相位调制)，就可称为衍射屏。

衍射屏的复振幅透过率(反射率)：衍射屏对入射光波的调制作用的数学描述，它是描述衍射屏宏观光学性质的函数，可用t(x,y)或r(x,y)表示。

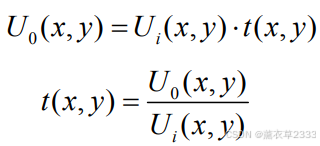
 t(x,y)可实可复，一般可表示为：

（1）当(x,y) = 常数时，但A(x,y) ≠ 常数时，只对入射光波的振幅进行调制，称为振幅型的

（2）当(x,y) ≠ 常数时，但A(x,y) = 常数时，只对入射光波的相位进行调制，称为相位型的

（3）当(x,y) ≠ 常数时，但A(x,y) ≠ 常数时，对入射光波的相位和振幅进行调制，称为复合型的

如：

① 光学均匀的平面平行玻璃板——相位型

② 非平行平面玻璃板，或非光学均匀的平行平面玻璃板——相位型

③ 各种不透明屏上的开孔——振幅型（单缝、双缝、矩孔、圆孔、光栅等）

④ 图像透过率片——振幅型，相位型或复合型

⑤ 空间光调制器——振幅型，相位型或复合型

3.2 衍射屏对角谱传播的影响

其中

是衍射屏函数的傅里叶变换。

卷积运算的展宽效应导致：

        衍射屏的引入使得入射光谱的角谱展宽，在出射光波中除了包含与入射光波相同方向传播的分量之外，还增加了一些与入射光波传播方向不同的平面波分量，即增加了一些高空间频率的平面波成分，这就是衍射波。

        空间受限的衍射屏，展宽了入射光波的角谱，空间受限越厉害，角谱展宽越大。

对于用单位振幅的平面波照射衍射屏这种特殊的情况：

        出射光波的角谱等于衍射屏函数的傅里叶变换，显然角谱分量大大增加了。