量子比特与量子门电路

白光白光

已于 2024-09-27 14:31:59 修改

阅读量815

点赞数 31

文章标签：量子计算

于 2024-09-20 18:55:00 首次发布

本文链接：https://blog.csdn.net/m0_54373077/article/details/142375532

版权

量子比特

纯态|0>，|1>，通用单量子比特表示

|ψ>=α|0>+β|1>，（1）

|1>的概率为|β>方，|0>概率为|α>方。可以用布洛赫球来表示单量子比特，

可将（1）式子改写为，

$|\psi\rangle=e^{i\gamma }(cos\frac{\Theta }{2})|0\rangle+e^{i\Phi }(sin\frac{\Theta }{2})|1\rangle )$

其中 $\Theta ,\Phi$ 定义了三维球上的一个点。测量会改变量子比特的状态，量子比特会发生坍塌，成为|0>或|1>态，所以只有在测量无数个量子比特后才能确定α和 β的值。

多量子比特

两量子比特|ψ>= $a_{00}$ |00>+ $a_{01}$ |01>+ $a_{10}$ |10>+ $a_{11}$ |11>，测量到x=(00,01,10,11)的概率为 $|a_{x}|^{2}$ ,测量后量子比特变为|x>，对第一个量子比特测量得到|0>的概率为 $|a_{00}|^{2}+|a_{01}|^{2}$ ，并且测量后状态发生改变。

量子门电路

在进一步讨论这个问题之前，我先对一些基本的概念作一个简介。

如前所述，在谈论量子计算时，我们谈的是n个 qubit ，对其执行一系列算符操作，最后执行测量。如下图，我们常常画出横着并排的n条直线，从左到右代表着时间顺序，而不同的直线代表不同的 qubit ；在这些直线上排列着各种小方块大方块还有竖线，代表着各种不同的单 qubit 或多 qubit 幺正算符，每一个幺正算符（满足性质 $U^{*}U=UU^{*}=I$ ）被称为一个（量子）门；人们常将一些简单的量子门组合成更复杂的量子门；整张图就被称为一个量子网络/量子电路。

人们给一些常用的量子门取了特定的名字，列举几个如下：

泡利X门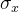 $\sigma _{x}$

$X=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$

作用在单qubit上，用于0，1翻转，相当于经典中的非门，在布洛赫球上相当于绕x轴旋转180度。

泡利Y门 $\sigma _{y}$

$Y=\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}$

对量子态施加 Y 门后，量子态在布洛赫球上的状态会绕 Y 轴旋转 180°。

泡利Z门 $\sigma _{z}$

$Y=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$

对量子态施加 Z 门后，量子态在布洛赫球上的状态会绕 Z 轴旋转 180°。

哈达玛门（Hadamard）——H门

$H=\frac{1}{\sqrt2}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}$

H门通常用来将纯态qubit，转变为纠缠态

$H|0\rangle=\frac{|0\rangle+|1\rangle}{\sqrt2}=|+\rangle$ ， $H|1\rangle=\frac{|0\rangle-|1\rangle}{\sqrt2}=|-\rangle$

相位门（phase gate）——S门

$H=\begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix}$

相位门（S 门）是对量子态的相位进行旋转的门，它可以看作是泡利Z 门的一般化。S门只对|1>作用，相当于绕y轴旋转 $\frac{\pi}{2}$ ， $S^{2}=Z$ ，两个S门相当于一个Z门

相位因子i即 $e^{\frac{i\Pi }{2}}$

Π/8门（T门）

$H=\begin{pmatrix} 1 & 0 \\ 0 & e^{\frac{i\Pi }{4}} \end{pmatrix}$

T 门，也称为 Π/8门，是一个相位旋转门，它将量子态的相位旋转 π/4，它是相位门的平方根门 $T^{2}=S$

受控非门——CNOT门

$CNOT=\begin{pmatrix} 1 & 0&0&0 \\ 0 &1&0&0\\0 &0&0&1\\0&0&1&0\end{pmatrix}$

对于 2 个量子比特系统，CNOT门实现如下功能。

如果控制比特为 ∣0〉，目标比特保持不变

如果控制比特为 ∣1〉，目标比特的状态翻转（即 ∣0〉↔∣1〉）

例如，对于输入状态 ∣10〉，控制比特 ∣1〉，目标比特从 ∣0〉 翻转为 ∣1〉，输出为 ∣11〉

CNOT 门可以用于纠缠态的生成，例如生成贝尔态。

交换门（SWAP Gate）

$CNOT=\begin{pmatrix} 1 & 0&0&0 \\ 0 &0&1&0\\0 &1&0&0\\0&0&0&1\end{pmatrix}$

交换门的作用就是交换两个量子比特的状态：

对输入状态 ∣ab〉其中 a 和 b 是 0 或 1），SWAP 门将其变为 ∣ba〉

例如，输入状态 ∣10〉通过 SWAP 门后，输出状态将是 ∣01〉

受控 Z 门（CZ Gate）

$CNOT=\begin{pmatrix} 1 & 0&0&0 \\ 0 &1&0&0\\0 &0&0&1\\0&0&1&0\end{pmatrix}$

当控制比特为 ∣0〉时，目标比特不变。

当控制比特为 ∣1〉时，对目标比特施加 Z 门，使其相位翻转。

例如，对于输入状态 ∣11〉，CZ 门将输出状态 −∣11〉，即施加了一个相位翻转。

CZ 门常用于生成纠缠态（如 GHZ 态）。它与 CNOT 门等价于局部单比特旋转后的结果。

另外还有受控相位门，Toffoli门（Controlled-Controlled-NOT 门，双比特控制门），Fredkin门（Controlled-SWAP 门，受控交换门）。

组合电路

就讲讲toffoli门吧，原来自己一直没有弄清楚。

先引入一些问题/实现目标

获得一个有着足够打维度希尔伯特空间中的量子态ψ；

对其执行任意的幺正算符Uψ；

对整个过程测量以得到经典的结果；

对整个过程进行经典的循环与判断。

而我们已知：

将n个二态系统相干的放在一起，可以得到一个有 $d=2^{n}$ 维的量子系统；

如何对单个比特执行任意的幺正算符，以及少量比特执行一些简单的幺正演化；

在n-qubit系统上任意复杂的测量都可以分解成一系列幺正算符和单qubit上的测量的叠加；

经典计算机是成熟的。

分解定理

定理1（单量子比特的分解）任何2×2的酉矩阵都可以分解为

$U=e^{i\alpha }\begin{pmatrix} e^{-i\beta } & 0 \\ 0 & e^{i\beta }\end{pmatrix}\begin{pmatrix} cos\frac{\gamma }{2} & sin\frac{-\gamma }{2} \\ sin\frac{\gamma }{2} & cos\frac{\gamma }{2}\end{pmatrix}\begin{pmatrix} e^{-i\delta } & 0 \\ 0 & e^{i\delta } \end{pmatrix}$

其中α，β，γ，δ为实数。

定理1的证明

既然U是幺正的，那么U的行向量和列向量是正交的，那么必然存在实数α，β，γ，δ满足

$U=\begin{pmatrix} e^{i(\alpha -\beta /2-\delta /2)}cos\frac{\gamma }{2} & -e^{i(\alpha -\beta /2+\delta /2)}sin\frac{\gamma }{2} \\ e^{i(\alpha +\beta /2-\delta /2)}sin\frac{\gamma }{2} & e^{i(\alpha +\beta /2+\delta /2)}cos\frac{\gamma }{2} \end{pmatrix}$

化简得

$U= e^{i\alpha }R_{z}(\beta )R_{y}(\gamma )R_{z}(\delta )$

推论4.2 设U是作用于单比特的酉门，那么存在对于单比特的酉算符A,B,C,满足 $ABC = I$ 和

$U = e^{i\alpha }AXBXC$ ，α是全局相位因子

Toffoli门（CCNOT门）

对于 CNOT 门另外一个推广的想法是，能不能实现两个门控制一个门？

定理3 任意幺正算符是可以开根号的，即对于任意幺正算符U，存在幺正算符V，使得 $V^{2}=U$

分解Toffoli门，一个一个情况分析

以110输入为例子，经过第一个V变换，第三条线受控，经过CNOT门，第一条线输入1，第二条线发生反转，经过 $V^{+}$ ，第二条线输入为0，不发生作用，经过第二个CNOT，发翻转，第二条线变成0，最后第一条线控制第二V变换，即 $V^{2}=U$ ，即得到了最终的效果U。（在做这些讨论时，始终要记住我们是对一个一般的量子态进行操作，也就是说上面这些情况是可以相干地同时发生的）