一、量子门电路:
本文主要集中实现NCT门集(NOT门,CNOT门,Toffoli门)中的量子门电路。
(1)NOT 门可以看成一个关于布尔函数的可逆映射,它将输入 𝑥 映射为输出 𝑥 + 1;
(2)CNOT 门可以看成一个关于二维布尔函数的可逆映射,它将输入 (𝑥1, 𝑥2) 映射为输出 (𝑥1, 𝑥1 + 𝑥2);
(3)Toffoli 门可以看成一个关于三维布尔函数的可逆映射,它将输入(𝑥1, 𝑥2, 𝑥3 ) 映射为输出 (𝑥1, 𝑥2, 𝑥3 + 𝑥1𝑥2)。
具体如下图所示:
![]()
(1)NOT门

(2)CNOT门

(3) Toffoli门
二、代码实现:
import matplotlib.pyplot as plt
import numpy as np
from qiskit import QuantumCircuit, assemble, Aer
from qiskit.quantum_info import Statevector
from qiskit.visualization import array_to_latex
from qiskit import transpile
from qiskit.providers.aer import QasmSimulator
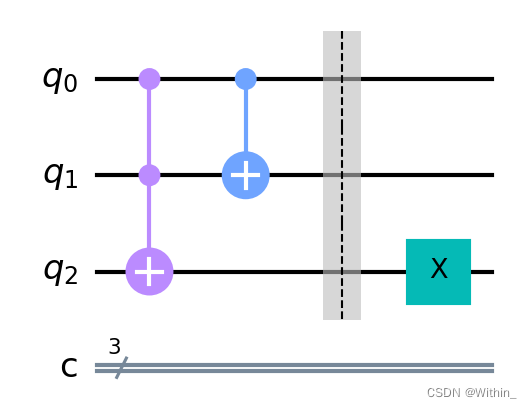
def U_f(circ):
circ.ccx(0, 1, 2)
circ.cx(0, 1)
circ.x(2)
return circ
def OneBit_Deutsh_Jozsa():
Circ = QuantumCircuit(3, 3)
Circ = U_f(Circ)
return Circ
Circ = OneBit_Deutsh_Jozsa()
Circ.draw('mpl')
plt.show()输出结果如下:

上图中,紫色表示的是Toffoli门,蓝色表示的是CNOT门,绿色表示的是NOT门。
若想要将两个步骤取消合并的状态(如上图的CNOT门和NOT门),可以在适当的位置添加
circ.barrier()即可。
结果如下所示:























 1937
1937

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








