蓝桥杯/洛谷：最长滑雪道/滑雪 + 扩展题目（记忆化搜索 Python）

本文链接：https://blog.csdn.net/m0_54689021/article/details/125457728

问题描述：

问题描述

　　小袁非常喜欢滑雪，因为滑雪很刺激。为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。小袁想知道在某个区域中最长的一个滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。如下：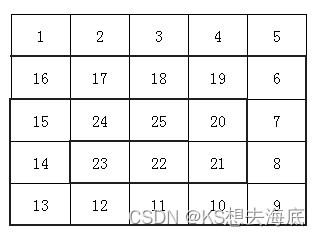

　　一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上，这是最长的一条。
　　你的任务就是找到最长的一条滑坡，并且将滑坡的长度输出。滑坡的长度定义为经过点的个数，例如滑坡24-17-16-1的长度是4。

输入格式

　　输入的第一行表示区域的行数R和列数C(1<=R, C<=10)。下面是R行，每行有C个整数，依次是每个点的高度h（0<= h <=10000）。

输出格式

　　只有一行，为一个整数，即最长区域的长度。

样例输入

5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

样例输出

分析：

解决一道题前首先考虑用什么算法

对于这道题而言最直接朴素的想法应该是对于每个点进行深搜或者广搜最后枚举一遍答案

但是注意对于每个点而言只要周围的点比他小都可以被走到因此这样做的话时间复杂度是指数级别的 AC不掉

那么我们考虑优化

首先搜索的思路是没有错的那么怎样优化它呢

我们观察到一个条件那就是某个点只能从数值更大的点转移过来也就是说整个答案序列应该是递减的 => 搜索时不可能出现循环 => 搜索顺序是具有拓扑结构的即在一个固定答案序列中数值较小的点一定是在数值较大的点后被搜索到那么我们就可以使用记忆化搜索了（注意上述所说：具有拓扑序是使用记忆化搜索的必备条件）

我们用一个数组储存从每个点出发可以达到的最大长度，之后，若是从其他数值较大的点转移到这个点时，不必再往后搜索了，因为结果已经记录在数组中了，直接返回就好

注：记忆化搜索可以看作普通搜索+大剪枝

上代码～～


n,m = map(int,input().split())
Map = []
ans = 0
for i in range(n) : Map.append(list(map(int,input().split())))
dp = [[-1 for i in range(m)]for j in range(n)]

def dfs(x,y) :
    global dp
    if dp[x][y] != -1 : return dp[x][y] # 搜索过了直接返回
    t = 1 # 最小就是1 即为本身
    
    for i,j in [(1,0),(0,1),(-1,0),(0,-1)] :
        px = x + i ; py = y + j
        if 0 <= px < n and 0 <= py < m and Map[px][py] < Map[x][y] :
            t = max(dfs(px,py)+1,t) # 更新当前点能到的最远距离
            
    dp[x][y] = t
    return t

for i in range(n) :
    for j in range(m) :
        dfs(i,j)
        
for i in range(n) :
    for j in range(m) :
        ans = max(ans,dp[i][j])
        
print(ans)

看到这里是不是对记忆化搜索有了深一步了解呢

再做一道拓展题巩固一下吧！

题目链接：691. 立方体IV - AcWing题库

分析过程完全相同只不过转移条件发生了小小的变化下一个点必须比上一个点大1

注意一下输出格式即可


T = int(input())

def dfs(x,y) :
    global dp
    if dp[x][y] != -1 : return dp[x][y]
    t = 1
    
    for i,j in [(1,0),(0,1),(-1,0),(0,-1)] :
        px = x + i ; py = y + j
        if 0<=px<S and 0<=py<S and Map[px][py] == Map[x][y] + 1 :
            t = max(t,dfs(px,py)+1)
    
    dp[x][y] = t
    return t
    
for _ in range(T) :
    S = int(input())
    Map = []
    for i in range(S) : Map.append(list(map(int,input().split())))
    dp = [[-1 for i in range(S)]for j in range(S)]
    ans = 0 ; idx = -1 
    
    for i in range(S) :
        for j in range(S) :
            dfs(i,j)
            
    for i in range(S) :
        for j in range(S) :
            if ans < dp[i][j] or ans == dp[i][j] and idx > Map[i][j] :
                ans = dp[i][j] ; idx = Map[i][j]
                
    txt = 'Case #{}: {} {}'
    print(txt.format(_,idx,ans))