层次分析法AHP

        层次分析法可以将难以定性分析或定量计算的问题转化成单一定量问题，将评估过程中的诸多问题分解出几个因素，然后把这些因素进行对比，区分出层次，逐一分析各个组成部分之间的联系，引入评定系数，最终得到一个有序的阶梯状层次，为评估提供可靠的定量依据，最后根据所有决 策属性对总体方案建立判断矩阵，进行最终计算。其原理是将与决策有关的因素分解成目标层、准则层、方案层等若干层次，通过对各因素的计算和比较，得出不同因素的权重，为决策者选择最优方案提供参考依据。

目录

1.建立层次结构模型

2.建立判断矩阵

3.一致性检验

4.计算权重

5.组合权重及结果分析

---

1.建立层次结构模型

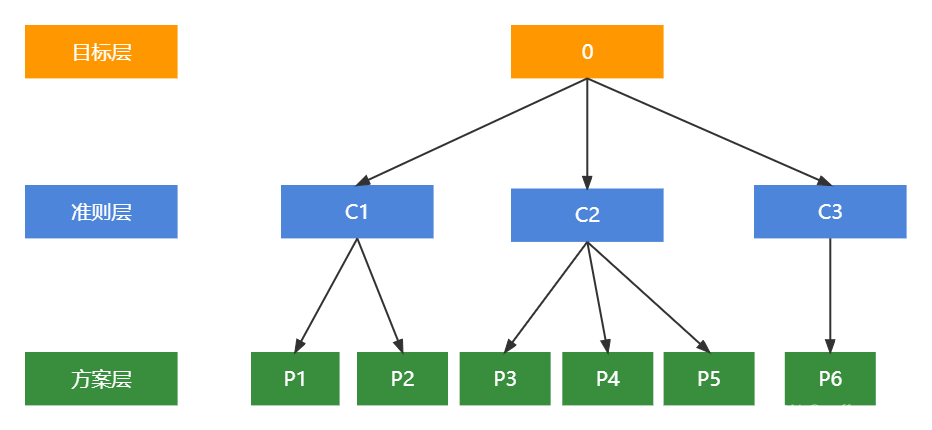
2.建立判断矩阵

        构造判断矩阵O-C：将C中的3个元素C1、C2、C3两两比较，得到两两比较矩阵（判断矩阵）。

O	C1	C2	C3
C1	1
C2		1
C3			1

         其中，任何矩阵应满足  , 判断矩阵中的一般都采用九分制标度法。

3.一致性检验

        对矩阵O-C进行一致性检验。

        step1：求O-C矩阵的特征值，从而求得一致性指标

        step2：根据下表查找对应的平均随机一致性指标RI

        step3： 计算一致性比例CR。

        若CR < 0.1，则判断矩阵的一致性可以接受；否则判断矩阵不一致，须对此修正。

4.计算权重

（1）算术平均法求权重。

 （2）几何平均法求权重

 （3）特征值法求权重

         为了增加结果的稳定性和严谨性，对三种方法进行求和并取平均值(当然，也可以直接使用方法之一)，可得C1、C2、C3各指标的权重。

        同理，构造判断矩阵O-C1、O-C2、O-C3并对其进行一致性检验，然后求其权重。

        例如，判断矩阵O-C1

C1	P1	P2
P1
P2

5.组合权重及结果分析

 （1）一级指标排序。方案层各元素对准则层的合成权重及结果。

准则层C1	方案层	排序
	P1
	P2

        从各个准则层分析结果。

（2）对目标层总排序。（即将方案层的全部指标进行排序）

目标层	准则层	方案层	排序

        对其结果分析。

参考资料：清风数学建模