深有体会:离散数学是算法的核心!!
章节 - “集合元素计数”,知识点“排斥定理” <=> "容斥定理";
本文章将以老师课堂上讲的案例:“1-1000中不能被5,6,8整除的数的个数”延伸至“从自然数1-n中不能被m个整数(非互质)整除的数的个数” 和 “从自然数1-n中至少被m个数中的一个数(非互质)整除的数的个数”。
说明:本文省略二项式定理的证明过程,直接引入定理和推论;文章代码采用二进制枚举表示每种选择方案,例如01001表示选择第0个和第3个性质集合的方案,那么相对应的1-n中满足性质的个数就等于(n / lcm(p[0],p[3])),以此类推;采用辗转相除法求解最大公约数,进而求解最小公倍数。
A. 引入定理3.2 中不具有性质
的元素数是:
B. 引入推论 在S中至少具有一条性质的元素数是:
案例1:求1-1000中不能被5,6,8整除的数的个数。
不妨设为自然数1000以内整数的集合,
、
、
分别表示三种性质(被5、6、8整除),对于
中的任意一个元素
,只能存在以下8(
)种情况:只具有性质
,只具有性质
,只具有性质
,同时具有性质
、
、/
、
/
、
(两种),同时具有/不具有性质
、
、
(三种);分别设
,
,
为满足
、
、
性质的元素的(小于等于1000)集合;
根据定理3.2,有式子如下:
规律:偶数次项数要减掉,奇数次项数要加;
注意:在没有声明哪些数是互质的情况下,
必然是满足被lcm(5,6)整除的数的集合。
C++代码如下:
// Author: 荣荣
// Time: 2023.10.21 09:53
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int p[3] = {5,6,8};
int n = 1000,res;
LL gcd(LL a,LL b) {return ((a % b == 0) ? b : gcd(b, a % b));}
LL lcm(LL a,LL b) {return ((a * b) / gcd(a,b));}
int main(){
for (int i = 1; i < (1 << 3); i ++){
int cnt = 0, pt = 1;
for (int j = 0; j < 3; j ++){
if (i >> j & 1){
cnt ++;
pt = lcm(pt, p[j]);
if (pt > n)
{
pt = -1;
break;
}
}
}
res = ((pt != -1) ? ((cnt & 1) ? res + n / pt : res - n / pt) : res);
}
cout << n - res << endl;
return 0;
}
输出结果:

推广案例1:求 中不能被
中不能被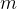 个整数(
个整数(](https://latex.csdn.net/eq?p%5Bi%5D%28p%5Bi%5D%20%5Cleq%2010%5E9%2Ci%20%5Cleq%20m%20%3D%2020%29) )整除的数的个数。
)整除的数的个数。
定理3.2,秒解。
C++代码如下:
// Author: 荣荣
// Time: 2023.10.21 09:53
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int M = 25;
int p[M];
int n,m,res;
LL gcd(LL a,LL b) {return ((a % b == 0) ? b : gcd(b, a % b));}
LL lcm(LL a,LL b) {return ((a * b) / gcd(a,b));}
int main(){
cin >> n >> m;
for (int i = 0; i < m; i ++) cin >> p[i];
for (int i = 1; i < (1 << m); i ++){
int cnt = 0;
LL pt = 1;
for (int j = 0; j < m; j ++){
if (i >> j & 1){
cnt ++;
pt = lcm(pt, p[j]);
if (pt > n)
{
pt = -1;
break;
}
}
}
res = ((pt != -1) ? ((cnt & 1) ? res + n / pt : res - n / pt) : res);
}
cout << n - res << endl;
return 0;
}
// 输入
1000000000 3
6000000 821123 98874522// 输出
999998607推论案例2:求 中被
中被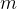 个整数(
个整数(](https://latex.csdn.net/eq?p%5Bi%5D%28p%5Bi%5D%20%5Cleq%2010%5E9%2Ci%20%5Cleq%20m%20%3D%2020%29) )中至少一个数整除的数的个数。
)中至少一个数整除的数的个数。
根据推论,秒解。
// Author: 荣荣
// Time: 2023.10.21 09:53
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int M = 25;
int p[M];
int n,m,res;
LL gcd(LL a,LL b) {return ((a % b == 0) ? b : gcd(b, a % b));}
LL lcm(LL a,LL b) {return ((a * b) / gcd(a,b));}
int main(){
cin >> n >> m;
for (int i = 0; i < m; i ++) cin >> p[i];
for (int i = 1; i < (1 << m); i ++){
int cnt = 0;
LL pt = 1;
for (int j = 0; j < m; j ++){
if (i >> j & 1){
cnt ++;
pt = lcm(pt, p[j]);
if (pt > n)
{
pt = -1;
break;
}
}
}
res = ((pt != -1) ? ((cnt & 1) ? res + n / pt : res - n / pt) : res);
}
cout << res << endl;
return 0;
}
// 输入
124552666 5
12312345 654652 546665 879465 21356464// 输出
573






















 1760
1760

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








