决策树简介
生活中的决策树
女孩相亲的决策树(源于网络,切勿当真)


让我们康康这个表格里的“?”该如何填充:
预测值1:根据女孩相亲决策树,年龄和长相都符合期望,于是收入甚至不用考虑,预测值1为:见。
预测值2:根据女孩相亲决策树,年龄符合,但长相不符合期望,于是收入不用考虑,预测值2为:不见。
预测值3:根据女孩相亲决策树,年龄不符合,于是长相和输入不用考虑,预测值3为:不见。
思考:(笔者会在文末给出答案,友友们也可以在评论区写写自己的理解❁´◡`❁)
1.女孩相亲过程中,更加看重哪些因素呢?
2.机器学习算法中,选择数据集的哪些特征进行分裂,效果会更好呢?
决策树概念
决策树是什么?
决策树是一种树形结构,树中每个内部节点表示一个特征上的判断,每个分支代表一个判断结果的输出,每个叶子节点代表一种分类结果。
决策树的建立过程:
1.特征选择:选取有较强分类能力的特征。
2.决策树生成:根据选择的特征生成决策树。
3.决策树也易过拟合,采用剪枝的方法缓解过拟合。
ID3决策树
信息熵
熵 Entropy :信息论中代表随机变量不确定度的度量。熵越大,数据的不确定性度越高,信息就越多;熵越小,数据的不确定性越低。

举个例子:
数据 α:ABCDEFGH
数据 β:AAAABBCD
明显:数据α 包含了 8 种信息,数据 β 包含了 4 种信息,则特征 α 的信息熵大于特征 β 的信息熵。
信息熵的计算较为复杂,下面给出它的计算方法:


信息增益
概念
特征a对训练数据集D的信息增益g(D,a),定义为集合D的熵H(D)与特征a给定条件下D的熵H(D|a)之差。
数学公式
g(D, a) = H(D)-H(D|A)
信息增益 = 熵 - 条件熵
条件熵

计算方法

ID3决策树的构建流程
1.计算每个特征的信息增益
2.使用信息增益最大的特征将数据集 拆分为子集
3.使用该特征(信息增益最大的特征)作为决策树的一个节点
4.使用剩余特征对子集重复上述(1,2,3)过程
信息增益案例




结论:活跃度的信息增益比性别的信息增益大,对用户流失的影响比性别大。
C4.5决策树
ID3决策树的不足
偏向于选择种类多的特征作为分裂依据
举个例子:

信息增益率
概念:
信息增益率 = 信息增益 /特征熵
计算方法:

信息增益率的本质:
特征的信息增益 ➗ 特征的内在信息
相当于对信息增益进行修正,增加一个惩罚系数
特征取值个数较多时,惩罚系数较小;特征取值个数较少时,惩罚系数较大。
惩罚系数:数据集D以特征a作为随机变量的熵的倒数。
小案例

CART决策树
CART决策树概念
CART决策树(Classification and Regression Tree)
Cart模型是一种决策树模型,它即可以用于分类,也可以用于回归。
Cart回归树使用平方误差最小化策略,
Cart分类生成树采用的基尼指数最小化策略。
基尼指数
基尼值Gini(D):从数据集D中随机抽取两个样本,其类别标记不一致的概率。故,Gini(D)值越小,数据集D的纯度越高。

基尼指数Gini_index(D):选择使划分后基尼系数最小的属性作为最优化分属性。

注意:
1.信息增益(ID3)、信息增益率值越大(C4.5),则说明优先选择该特征。
2.基尼指数值越小(cart),则说明优先选择该特征。
小案例





三种决策树的区别

案例
泰坦尼克号乘客生存预测案例
数据下载: https://pan.baidu.com/s/1PasiSSK2xpSYDSmen6T4Ug?pwd=wrgu 提取码: wrgu
案例背景
泰坦尼克号沉没是历史上最著名的沉船事件。1912年4月15日,在她的处女航中,泰坦尼克号在与冰山相撞后沉没,在2224名乘客和船员中造成1502人死亡。这场耸人听闻的悲剧震惊了国际社会,并为船舶制定了更好的安全规定。 造成海难失事的原因之一是乘客和船员没有足够的救生艇。尽管幸存下来有一些运气因素,但有些人比其他人更容易生存,例如妇女,儿童和社会地位较高的人群。 在这个案例中,我们要求您完成对哪些人可能存活的分析。数据集中的特征包括票的类别,是否存活,乘坐班次,姓名,年龄,上船港口,房间,性别等。

决策树api介绍
class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
-
criterion
-
特征选择标准
-
"gini"或者"entropy",前者代表基尼系数,后者代表信息增益。一默认"gini",即CART算法。
-
-
min_samples_split
-
内部节点再划分所需最小样本数
-
这个值限制了子树继续划分的条件,如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。我之前的一个项目例子,有大概10万样本,建立决策树时,我选择了min_samples_split=10。可以作为参考。
-
-
min_samples_leaf
-
叶子节点最少样本数
-
这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数,或者最少样本数占样本总数的百分比。如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。之前的10万样本项目使用min_samples_leaf的值为5,仅供参考。
-
-
max_depth
-
决策树最大深度
-
决策树的最大深度,默认可以不输入,如果不输入的话,决策树在建立子树的时候不会限制子树的深度。一般来说,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间
-
-
random_state
-
随机数种子
-
案例实现
相比其他学习模型,决策树在模型描述上有巨大的优势,决策树的逻辑推断非常直观,具有清晰的可解释性,也有很方便的模型的可视化。在决策树的使用中,无需考虑对数据量化和标准化,就能达到比较好的识别率。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report, precision_score, recall_score, f1_score, roc_auc_score
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
"""
演示决策树分层
"""
# 1、读取数据
train_df = pd.read_csv("data/train.csv")
train_df.info()
# 2、数据预处理
# 2-1 获取特征列 和标签列 船舱等级 、 性别 、年龄
x = train_df[['Pclass', 'Sex', 'Age', 'Embarked', 'Ticket']]
y = train_df['Survived']
# 2-2 用age 处理 age列求平均值
x['Age'] = x['Age'].fillna(x['Age'].mean())
# 2-3 查看数据
# x.info()
print(x.head(5))
# 分析 age需要处理 采用热编码
x = pd.get_dummies(x)
print(x.head(5))
x.drop('Sex_male', axis=1, inplace=True)
print(x.head(5))
# 拆分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=24)
print(x_train.head(5))
# 是否需要特征工程
f = StandardScaler()
x_train = f.fit_transform(x_train)
x_test = f.transform(x_test)
# 4训练模型
model = DecisionTreeClassifier(criterion="gini")
model.fit(x_train, y_train)
y_pre = model.predict(x_test)
print(f"打印预测结果{y_pre}") # 0已故 1 活着
# 模型评估
print(f"准确率:{model.score(x_test, y_test)}")
print(f"精确率:{precision_score(y_test, y_pre)}")
print(f"召回率:{recall_score(y_test, y_pre)}")
print(f"F1:{f1_score(y_test, y_pre)}")
print(f"ROC_AUC:{roc_auc_score(y_test, y_pre)}")
print(f"分类报告{classification_report(y_test, y_pre, target_names=['Died', 'Survivor'])}")
# TODO 绘CART决策树图
# TODO 1设置画布大小
plt.figure(figsize=(50, 30))
# TODO 2.绘制决策树
# decision_tree:决策树模型 filled 填充颜色
# 注意: 可以提前设置层数 max_depth=15,达到预剪枝效果!!!
plot_tree(model, filled=True)
# TODO 3.保存图片
plt.savefig('data/cart.png')
# TODO 4.展示图片
plt.show()
代码运行结果

CART回归树
CART 回归树和 CART 分类树的不同之处
1. CART 分类树预测输出的是一个离散值,CART 回归树预测输出的是一个连续值。
2. CART 分类树使用基尼指数作为划分、构建树的依据,CART 回归树使用平方损失。
3. 分类树使用叶子节点里出现更多次数的类别作为预测类别,回归树则采用叶子节点里均值作为预测输出
CART回归树的平方损失

举个例子




线性回归和回归决策树的对比案例
案例分析
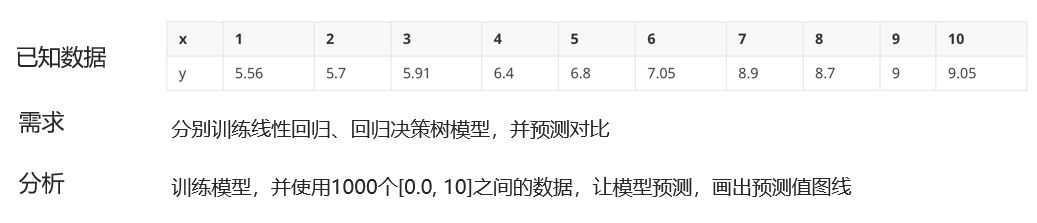

从预测效果来看:
1、线性回归是一条直线
2、决策树是曲线
3、树的拟合能力是很强的,易过拟合
案例实现
# 导包.
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeRegressor # 回归决策树
from sklearn.linear_model import LinearRegression # 线性回归
import matplotlib.pyplot as plt # 绘图
# 解决中文乱码问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 1. 获取数据.
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])
# print(x)
# print(y)
# 2. 创建线性回归 和 决策树回归模型.
estimator1 = LinearRegression() # 线性回归
estimator2 = DecisionTreeRegressor(max_depth=1) # 回归决策树, 层数=1
estimator3 = DecisionTreeRegressor(max_depth=3) # 回归决策树, 层数=3
# 3. 训练模型.
estimator1.fit(x, y)
estimator2.fit(x, y)
estimator3.fit(x, y)
# 4. 准备测试数据, 用于测试.
# 起始, 结束, 步长.
x_test = np.arange(0.0, 10.0, 0.1).reshape(-1, 1)
# print(x_test)
# 5. 模型预测.
y_predict1 = estimator1.predict(x_test)
y_predict2 = estimator2.predict(x_test)
y_predict3 = estimator3.predict(x_test)
# 6. 绘图
plt.figure(figsize=(10, 5))
# 散点图(原始的坐标)
plt.scatter(x, y, color='gray', label='data')
# 线性回归的预测结果
plt.plot(x_test, y_predict1, color='r', label='liner regression')
# 回归决策树, 层数=1
plt.plot(x_test, y_predict2, color='b', label='max depth=1')
# 回归决策树, 层数=3
plt.plot(x_test, y_predict3, color='g', label='max depth=3')
# 显示图例.
plt.legend()
# 设置x轴标签.
plt.xlabel('data')
# 设置y轴标签.
plt.ylabel('target')
# 设置标题
plt.title('回归决策树和线性回归可视化对比')
# 保存图片
plt.savefig('data/line_rtree.png')
# 显示图片
plt.show()运行结果

决策树 剪枝
决策树正则化
我们在之前的知识里已经知道,模型有时会出现过拟合的情况,这时我们需要采取措施来缓解,以让模型达到相对较好的拟合状态,在线性回归模型里,我重点介绍了两种缓解过拟合的方法,即L1正则化和L2正则化缓解过拟合,感兴趣的友友可以点击文末的链接,温习一下正则化的概念和案例。
对于决策树模型,也会存在过拟合问题,这时我们会用到决策树正则化,即剪枝。
挑选西瓜案例
剪枝思想

剪枝原理
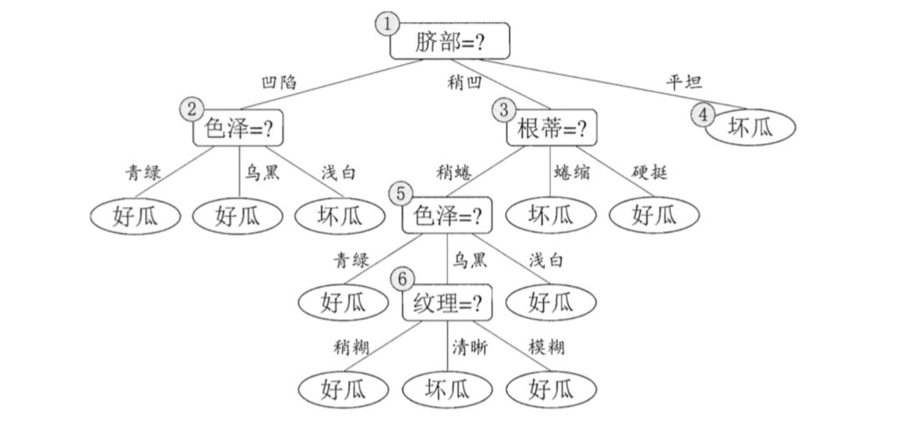
预剪枝和后剪枝补充
预剪枝(Pre-pruning)
- 定义:在决策树构建过程中,通过某些规则提前停止树的生长。
- 剪枝时机:在生成节点时即时判断是否继续分裂。
- 常见停止条件:
- 当前节点的样本数低于阈值。
- 分裂后的性能提升(如信息增益、基尼系数)小于阈值。
- 树的深度达到预设最大值。
- 节点中样本的类别纯度(如95%属于同一类)。
- 优点:
- 训练速度快(避免生成复杂树后再剪枝)。
- 降低过拟合风险,模型更简单。
- 缺点:
- 可能欠拟合(过早停止可能导致关键分裂被忽略)。
- 依赖阈值设定,需调参(如最大深度、最小样本数)。
2. 后剪枝(Post-pruning)
- 定义:先让决策树完全生长,再根据一定规则从底部向上剪去子树。
- 剪枝时机:树构建完成后,对非叶节点进行考察。
- 常见方法:
- 代价复杂度剪枝(CCP):如CART树的α参数,平衡子树复杂度与误差。
- 错误率降低剪枝(REP):用验证集测试剪枝前后错误率。
- 悲观剪枝(PEP):基于统计检验(如卡方检验)判断节点是否冗余。
- 优点:
- 保留更多有用分裂,泛化能力通常优于预剪枝。
- 对噪声数据更鲁棒。
- 缺点:
- 计算成本高(需先生成完整树)。
- 可能需要额外验证集(如REP)。
预剪枝-西瓜挑选案例
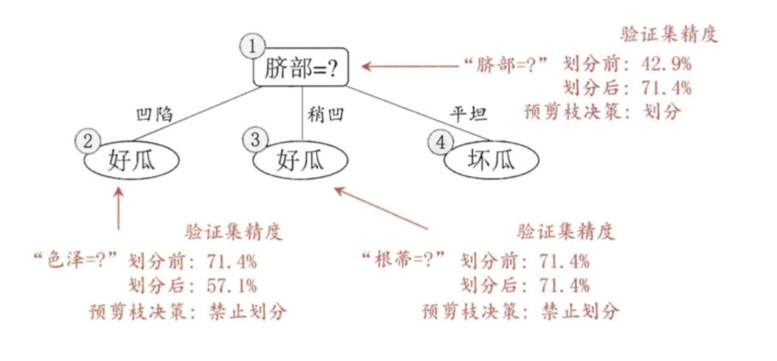
基于预剪枝策略从上表数据所生成的决策树如上图所示,其验证集精度为 71.4%.
后剪枝-西瓜挑选案例

先利用训练集完整的生成一颗树,有6个内部节点。分别考察这些节点作为叶子节点模型的准确率,若准确率上升,则剪掉,否则保留。
决策树两种正则化方法对比:

尾声
行文至此,虽然身体和心理上都很累,但是想到马上要发布此篇博文,就会觉得一切都值得<( ̄︶ ̄)↗[GO!]
接下来,我来回答一下上文提到的两个问题:
1、女孩相亲过程中,更看重哪些特征呢?
年龄 > 长相 > 收入 > 是否公务员
2、机器学习算法中,选择数据集中的哪些特征进行分裂,会更好呢?
本文提到的ID3决策树、C4.5决策树、CART决策树的构建过程的开始就是选择特征进行分裂,显然信息增益、信息增益率、基尼指数都是用来评估特征的,得分高者优先被选择去用来分裂,如信息增益率高的特征会优先被选择。
最后,将系列的前几篇文章的链接附在下面,供友友们参考:




























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








