散点拟合曲线方程，并求点到曲线的最小距离

1、通过散点拟合出曲线方程并绘制出图形：

#coding=utf-8

import matplotlib.pyplot as plt
import numpy as np
 
x = [-1675, -1662, -1648, -1632, -1616, -1602, -1590, -1579, -1567, -1556, -1545, -1534, -1525, -1515, -1506, -1496, -1485, -1473, -1462, -1450, -1439, -1428, -1417, -1405, -1399, -1389, -1379]
y = [-3902, -3865, -3825, -3776, -3724, -3673, -3629, -3583, -3532, -3484, -3428, -3375, -3326, -3269, -3221, -3167, -3114, -3050, -2990, -2927, -2868, -2808, -2750, -2684, -2653, -2600, -2547]
z1 = np.polyfit(x, y, 4) #用4次多项式拟合，输出系数从高到0
#print(z1)
p1 = np.poly1d(z1) #使用次数合成多项式
y_pre = p1(x)
 
plt.plot(x,y,'.')
plt.plot(x,y_pre)
plt.show()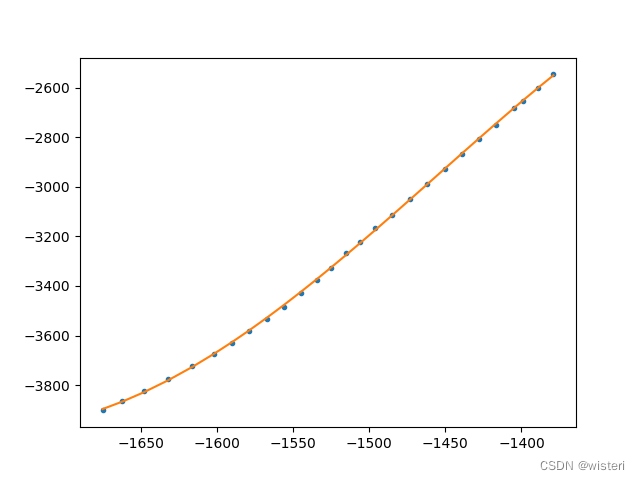

 2、求点到拟合曲线的最小距离并绘图显示

#coding=utf-8

import numpy as np  
import matplotlib.pyplot as plt
 
x = [-1675, -1662, -1648, -1632, -1616, -1602, -1590, -1579, -1567, -1556, -1545, -1534, -1525,
 -1515, -1506, -1496, -1485, -1473, -1462, -1450, -1439, -1428, -1417, -1405, -1399, -1389, -1379]
y = [-3902, -3865, -3825, -3776, -3724, -3673, -3629, -3583, -3532, -3484, -3428, -3375, -3326,
 -3269, -3221, -3167, -3114, -3050, -2990, -2927, -2868, -2808, -2750, -2684, -2653, -2600, -2547]
z1 = np.polyfit(x, y, 4) #用4次多项式拟合，输出系数从高到0
p1 = np.poly1d(z1) #使用次数合成多项式

def distance(x, y, x0, y0):
    """
    Return distance between point
    P[x0,y0] and a curve (x,y)
    """
    d_x = x - x0
    d_y = y - y0
    dis = np.sqrt( d_x**2 + d_y**2 )
    return dis

def min_distance(x, y, P, precision=5):
    """
    Compute minimum/a distance/s between
    a point P[x0,y0] and a curve (x,y)
    rounded at `precision`.
    
    ARGS:
        x, y      (array)
        P         (tuple)
        precision (int)
        
    Returns min indexes and distances array.
    """
    # compute distance
    d = distance(x, y, P[0], P[1])
    d = np.round(d, precision)
    # find the minima
    glob_min_idxs = np.argwhere(d==np.min(d)).ravel()
    return glob_min_idxs, d

def f(x):
    return p1(x)

x = np.linspace(-1700, -1200, 1000)
y = f(x)

P = (-1662, -3848)

min_idxs, dis = min_distance(x, y, P)

fig, ax = plt.subplots(figsize=(7, 7))

ax.plot(x, y, lw=4)
for idx in min_idxs:
    ax.plot(
        [P[0], x[idx]],
        [P[1], y[idx]],
        '--', lw=1,
        label=f'distance {dis[idx]:.2f}'
    )
ax.plot(*P, 'or')
ax.text(
    P[0], P[1], 
    f"  P ({P[0]}, {P[1]})", 
    ha='left', va='center',
    fontsize=15
)
ax.set(
    xlim=(-1700, -1200),
    ylim=(-4000, -2400),
)
ax.legend()
plt.show()

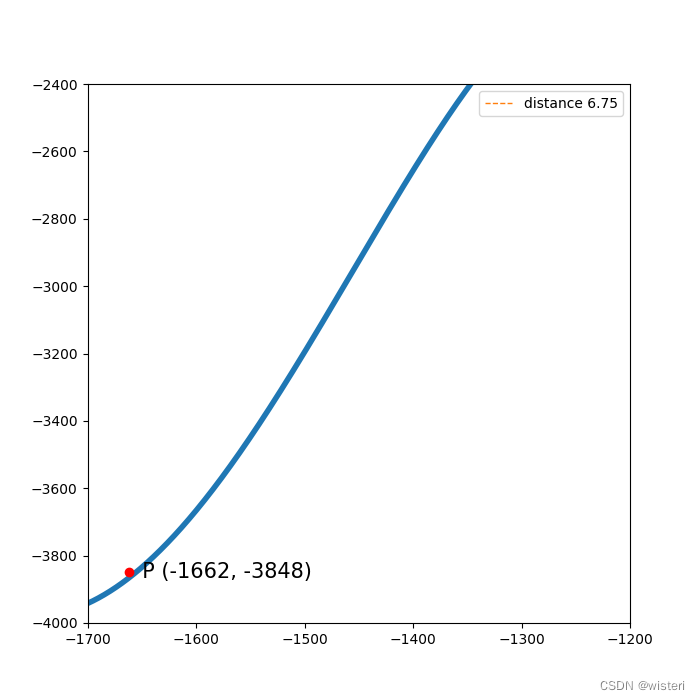
 3、返回点到拟合曲线的最小距离值

#coding=utf-8

import numpy as np  
import matplotlib.pyplot as plt
 
x = [-1675, -1662, -1648, -1632, -1616, -1602, -1590, -1579, -1567, -1556, -1545, -1534,
 -1525, -1515, -1506, -1496, -1485, -1473, -1462, -1450, -1439, -1428, -1417, -1405, -1399, -1389, -1379]
y = [-3902, -3865, -3825, -3776, -3724, -3673, -3629, -3583, -3532, -3484, -3428, -3375,
 -3326, -3269, -3221, -3167, -3114, -3050, -2990, -2927, -2868, -2808, -2750, -2684, -2653, -2600, -2547]
z1 = np.polyfit(x, y, 4) #用4次多项式拟合，输出系数从高到0
f1 = np.poly1d(z1) #使用次数合成多项式

def distance(x, y, x0, y0):
    """
    Return distance between point
    P[x0,y0] and a curve (x,y)
    """
    d_x = x - x0
    d_y = y - y0
    dis = np.sqrt( d_x**2 + d_y**2 )
    return dis

def min_distance(x, y, P, precision=5):
    """
    Compute minimum/a distance/s between
    a point P[x0,y0] and a curve (x,y)
    rounded at `precision`.
    
    ARGS:
        x, y      (array)
        P         (tuple)
        precision (int)
        
    Returns min indexes and distances array.
    """
    # compute distance
    d = distance(x, y, P[0], P[1])
    d = np.round(d, precision)
    # find the minima
    glob_min_idxs = np.argwhere(d==np.min(d)).ravel()
    return glob_min_idxs, d

def f1_min_distance(P):
    x = np.linspace(-1700, -1200, 1000)
    y = f1(x)

    min_idxs, dis = min_distance(x, y, P)
    return min(dis)


if __name__ == '__main__':
    P = (-1662, -3848)
    d = f1_min_distance(P)
    print(d)

返回值 f1_min_distance(P) = 6.74534