【FFT】数据点数是否一定为2的n次方？不补零会如何处理？

毓橙咲

于 2024-12-01 10:46:59 发布

阅读量2.1k

点赞数 30

分类专栏： FFT 文章标签： FFT 补零

本文链接：https://blog.csdn.net/m0_57407372/article/details/144135983

版权

FFT 专栏收录该内容

18 篇文章

订阅专栏

一般来说，FFT的数据点个数为以2为基数的整数次方（采用以2为基的FFT算法，可以提升运算性能），但是并没有要求FFT的数据点个数一定为2的n次方。

因此针对数据点数不是以2为基数的整数次方，有两种处理方法：①在原始数据开头或者末尾补零，将数据补到以2为基数的整数次方；②采用以任意数为基数的FFT算法。

那接下来就两种处理方法进行说明，分析优点与缺点。

举例：假设输入一个信号 $f(x)=cos(2\pi \times 1000000t)+cos(2\pi \times 1050000t)$ ，可以看出该信号中包含了两个不同频率的余弦信号， $f_{1}=1MHz$ , $f_{2}=1.05MHz$ 。假设采样频率 $F_{S}=100MHz$ 。

1. 不补零FFT

如果采1000个点，那么时域信号的时长就为 $T=1000*(1/F_{s})=10\mu s$ ，如下图左所示。直接对1000个点进行FFT，不进行补零操作，就可得到如下图右所示。

由上图可知，频谱点较为稀疏，在1MHz附近根本无法将1 MHz 和1.05 MHz 的两个频率分开。这是由于频率分辨率不够。那么，如何提高频率分辨率呢？

频率分辨率分为两种，一种是波形分辨率，另外一种为视觉分辨率（FFT分辨率）

①波形分辨率：由原始数据的时间长度决定

$\Delta R_{w}=\frac{1}{T}$

②视觉分辨率（FFT分辨率）：由采样频率和参与FFT的数据点数决定

$\Delta R_{fft}=\frac{F_{s}}{N_{fft}}$

注意：当不进行补零操作时，上述两种分辨率是相等的，如下公式所示。

$\Delta R_{w}=\frac{1}{10\mu s}=\Delta R_{fft}=\frac{100MHz}{1000}=100kHz$

2. 补零FFT

在上述1000个数据点个数的基础上补零至7000个，那么该信号如下图左所示。那么进行补零后的FFT结果如下图右所示。

由上图可知，频谱点密集了，但是还是无法把在1MHz附近的1 MHz 和1.05 MHz 的两个频率分开。这是因为波形分辨率为100kHz（ $\Delta R_{w}=\frac{1}{T}=\frac{1}{10\mu s}=100kHz$ ），大于1 MHz 和1.05 MHz之间距离的50kHz，且波形分辨率只与原始数据的时长T有关，与参与FFT的数据点数无关，因此补多少零都无用。

但是补零的频谱图相比于不补零的频谱图，其频域曲线更加光滑，即增加另外一个分辨率，即FFT分辨率。因此“时域补零相当于频域插值”，时域补零相当于在频域增加了插值点数。

3. 增加采样数据点数不补零

因此为了进一步区分1MHz附近的1 MHz 和1.05 MHz 的两个频率，需要改变原始数据的时长T。在采样频率不变（ $F_{S}=100MHz$ ）的情况下，如果采7000个点，那么时域信号的时长就为 $T=7000*(1/F_{s})=70\mu s$ ，如下图左所示。对其进行FFT处理后得到的结果为下图右所示。

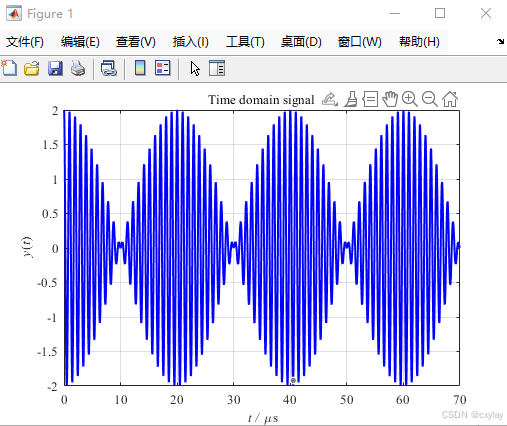
波形分辨率为： $\Delta R_{w}=\frac{1}{T}=\frac{1}{70\mu s}\approx 14kHz$ ，小于1 MHz 和1.05 MHz之间距离的50kHz，因此可以区分两者。

解决了区分两种频率的问题，又出现了一个新的问题。

上图中可以清晰地看出，1MHz对于的幅值为1，与原始信号中该频率成分的幅值一致，但是1.05MHz对应的幅值和原始信号的幅值不一致，明显低于1，但是其周边的点却有较大的幅值，这就是频谱泄露。

4. 增加采样数据点数并补零

频谱泄露: 因为数据点的个数，使得在1MHz处有谱线存在，而在1.05MHz处却没有，使得测量结果偏离实际值，同时在实际频率点的能量分散在两侧的其他频率点上，并出现一些幅值较小的假谱。

因此，我们需要设法让谱线同时经过1MHz和1.05MHz，找到两者的公约数,1MHz=80×12.5kHz；1.05MHz=84×12.5kHz，为两个频率的公约数。FFT分辨率为 $\Delta R_{fft}=\frac{F_{s}}{N_{fft}}=\frac{100MHz}{8000}=12.5kHz$ ，因此进行补零操作，在原始数据7000个的基础上补零至8000个数据点数，如下图左所示。对其FFT后，结果如下图右所示。