目录
第三章 极限导论
3.1 极限：基本思想
1. f(x)=x-1, x≠2
读作：当x趋于2，f(x)的极限等于1
2. 
g(2)的值与该极限不相关。只有那些在x接近于2时的g(x)的值，而不是在2处的值，才是问题的关键。
3. 
中，变量x只是一个虚拟变量。它是一个暂时的标记，用来表示某个非常接近于2的量，可以被替换成其他任意字母，只要替换是彻底的；同样，当你求出极限的值时，结果不可能包含这个虚拟变量。
也可写作： 
3.2 左极限与右极限
1. h(x)在x=3的左极限等于1，在x=3的右极限等于-2
2. 双侧极限在x=a处存在，仅当左极限和右极限在x=a处都存在且相等。
等价于 
3. 如果左极限和右极限不相等，则双侧极限不存在，写作 （缩写DNE表示“不存在”）
3.3 何时不存在极限
1. 
左极限和右极限不相等，故双侧极限不存在
2. 
3. 左极限或右极限也可能不存在
在x=0附近很杂乱，它无限地在1和-1之间振荡，没有垂直渐近线，也没有极限。因此可以说 不存在（DNE）。
3.4 在∞和-∞处的极限
1. 
不存在（DNE）
2. 大的数和小的数
如果一个数的绝对值是非常大的数，则这个数是大的；
如果一个数非常接近于0（但不是真的等于0），则这个数是小的
多大才是“足够大”？取决于你想让f(x)距离L有多近。100在左图足够大，而在右图就不是足够大。
用术语“在∞附近”代替“大的正的数”
3.5 关于渐近线的两个常见误解
1. 一个函数不一定要在左右两边有相同的水平渐近线。
一个函数可以有不同的右侧和左侧水平渐近线，但最多只能有两条水平渐近线（一条在右侧，另一条在左侧），也可能一条都没有或者只有一条。这和垂直渐近线相反：一个函数可以有很多条垂直渐近线（如y=tan(x)）。
2. 一个函数可能和它的渐近线相交。
考虑定义为f(x)=sin(x)/x的函数f，sin(x)的值在-1和1之间振荡，sin(x)/x的值在曲线y=-1/x和y=1/x之间振荡。
，x轴是f的水平渐近线，且y=f(x)的图像一次又一次与x轴相交。
3.6 三明治定理
1. 三明治定理（又称作夹逼定理）：如果一个函数f被夹在函数g和h之间，当x→a时，这两个函数g和h都收敛于同一个极限L，那么当x→a时，f也收敛于极限L。
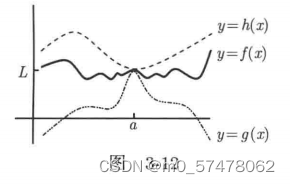
2. 对于单侧极限，同理。如 
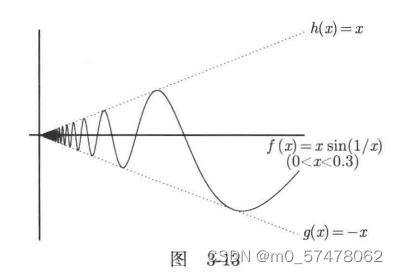
3. 
这也适用于左极限或右极限；在那种情况下，不等式只需要在a的相应一侧对于x成立即可。当a是∞或-∞时也适用；在那种情况下，要求对于所有的非常大的x，不等式成立。
3.7 极限的基本类型小结
1. x=a时的右极限
2. x=a时的左极限
3. x=a时的双侧极限
4. x→∞时的极限
5. x→-∞时的极限
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
