目录
方法二:头插法public void addFirst(int data)
方法三:尾插法public void addLast(int data)
4.查找是否包含关键字key是否在单链表当中:public boolean contains(int key)
6.任意位置插入,第一个数据节点为0号下标:public boolean addIndex(int index,int data)
7.删除第一次出现关键字为key的节点:public void remove(int key)
8.删除所有值为key的节点:public void removeAllKey(int key)
概念
链表(linked list):是一种物理存储结构上非连续存储结构,数据元素的逻辑顺序是通过链表中的引用链接次序实现的.
链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
链表的分类
- 单向链表,双向链表
- 带头链表,不带头链表
- 循环的,非循环的
排列组合后一共有
即一共8种链表,其中单向、不带头、非循环以及双向、不带头、非循环的链表最为重要,也是本文主要介绍的链表类型。
链表的结构
对于链表的结构,可以用如下这个图来模拟。
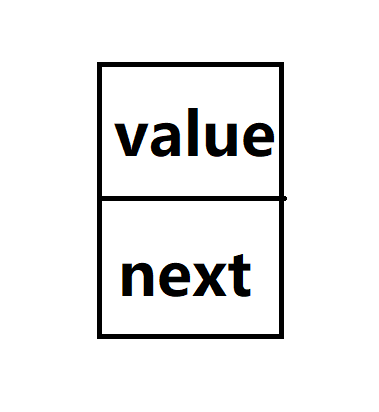
图中所示的为链表的一个节点,value是这个节点的所存储的数据值,next为下一节点的地址。
下面是一个5个节点的链表。

接下来,我们来实现这样的链表的增删查改:
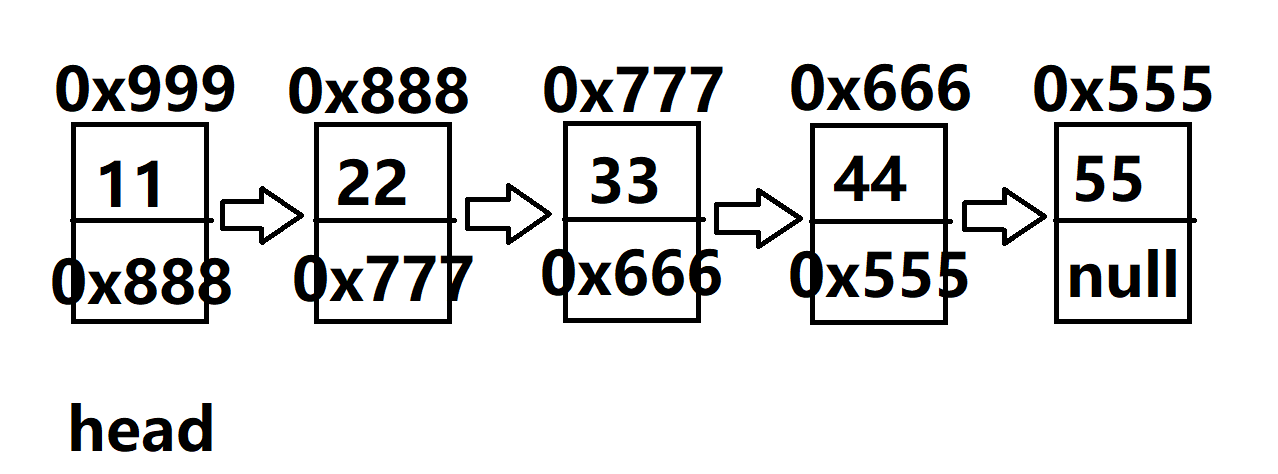
第一个节点,地址假设是0x999,存储的数据是11,next存储的是下一个节点的地址(假设是0x888)
第二个节点,地址假设是0x888,存储的数据是22,next存储的是下一个节点的地址(假设是0x777)
第三个节点,地址假设是0x777,存储的数据是33,next存储的是下一个节点的地址(假设是0x666)
第四个节点,地址假设是0x666,存储的数据是44,next存储的是下一个节点的地址(假设是0x555)
第五个节点,地址假设是0x555,存储的数据是55,由于没有后续节点,next存储的是空指针null
定义一个head,存储头节点(第一个节点)的地址(假设为0x999)。
代码实现链表
1.创建节点类
节点由val域(数据域),以及next域(指针域)组成,对于next域,其是引用类型,存放下一个节点的地址,故
用public ListNode next来创建next。
同时设置构造函数,方便对val进行初始化。
//ListNode代表一个节点
class ListNode{
public int val;
public ListNode next;
//构造函数
public ListNode(int a){
this.val = a;
}
}2.创建链表
-
方法一:枚举法(略简单,略low)
public class MyLinkedList {
public ListNode head;//链表的头
public void creatList(){
ListNode listNode1 = new ListNode(11);
ListNode listNode2 = new ListNode(22);
ListNode listNode3 = new ListNode(33);
ListNode listNode4 = new ListNode(44);
ListNode listNode5 = new ListNode(55);
this.head = listNode1;
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
listNode4.next = listNode5;
}
}直接进行val的赋值以及对next的初始化。
注意:不用对最后一个节点的next进行赋值,因为next是引用类型,不赋值则默认为null。
-
方法二:头插法public void addFirst(int data)
头插法是指在链表的头节点的位置插入一个新节点,定义一个node表示该节点,然后就是对node的next进行赋值,用node.next = this.head即可完成(注意:head应指向新节点)
代码实现
public void addFirst(int data){
ListNode node = new ListNode(data);
node.next = this.head;
this.head = node;
}-
方法三:尾插法public void addLast(int data)
尾插法是指在链表的尾节点的位置插入一个新节点,定义一个node表示该节点,然后就是对原来最后一个节点的next进行赋值,先将head移动至原来最后一个节点,用head.next = node进行赋值(注意,如果链表不为空,需要定义cur来代替head)
代码实现
public void addLast(int data){
ListNode node = new ListNode(data);
if(this.head == null){
this.head = node;
}else {
ListNode cur = this.head;
while(cur.next != null){
cur = cur.next;
}
cur.next = node;
}
}3.打印链表:public void display()
认识了链表的结构,我们可以知道,节点与节点之间通过next产生联系。并且我们已将创建了head,即头节点的地址,通过head的移动来实现链表的打印。
注意:为了使head一直存在且有意义,我们在display()函数中定义一个cur:ListNode cur = this.head;来替代head。
对于head的移动,可用head = head.next来实现。
代码实现:
public void display(){
ListNode cur = this.head;
while(cur != null){
System.out.print(cur.val+" ");
cur = cur.next;
}
System.out.println();
}4.查找是否包含关键字key是否在单链表当中:public boolean contains(int key)
查找key,可以利用head移动,实现对于key的查找(注意:同样要定义一个cur来代替head)
代码实现
public boolean contains(int key){
ListNode cur = this.head;
while(cur != null){
if(cur.val == key){
return true;
}
cur = cur.next;
}
return false;
}5.得到单链表的长度:public int Size()
定义计数器count = 0,通过head的移动来判断链表长度(注意:同样要定义一个cur来代替head)
代码实现
public int Size(){
int count = 0;
ListNode cur = this.head;
while(cur != null){
count++;
cur = cur.next;
}
return count;
}6.任意位置插入,第一个数据节点为0号下标:public boolean addIndex(int index,int data)
比如,我们把一个值为1314,地址是0x520(设为node引用)的节点,即val域值为1314,next域为null,地址是520,将该节点插入至3号位置,

经过分析,需要将head先移至2号位置(注意:用cur代替head,防止head丢失),然后
node.next = cur.next使该节点的next域改为下一节点的地址,再cur.next = node.next使前一节点
的next域改为该节点的地址。
public void addIndex(int index,int data){
if(index < 0 ||index > Size()){ //对index位置的合法性进行判断
return;
}
if(index == 0){ //相当于头插法
addFirst(data);
return;
}
if(index = Size()){ //相当于尾插法
addLast(data);
return;
}
ListNode cur = findIndex(index);//找到index位置前一位置的地址
ListNode node = new ListNode(data);//初始化node
node.next = cur.next;
cur.next = node;
}7.删除第一次出现关键字为key的节点:public void remove(int key)
对于删除第一次出现的key值的节点,若不是头节点,我们只需将key值对应的节点的前一节点的next的域改为key值对应的节点的next域即可。
对于头节点,直接head = head.next即可。
对于key值对应的节点的前一节点,我们可以写一个函数来找到它,方便后续的代码书写。
//找到key的前驱(前一节点)
public ListNode searchPrev(int key){
ListNode cur = this.head;
while(cur.next != null){
if(cur.next.val == key){
return cur;
}
cur = cur.next;
}
return null;
}
//删除第一次出现关键字为key的节点
public void remove(int key){
if(this.head == null){
return;
}
if(this.head.val == key){
this.head = this.head.next;
return;
}
ListNode cur = searchPrev(key);
if(cur == null){
return; //没有要删除的节点
}
ListNode del = cur.next;//定义要删除的节点
cur.next = del.next;
}8.删除所有值为key的节点:public void removeAllKey(int key)
若要删除所有值为key的节点,其实我们只需多次调用上面所写的remove函数即可完成,但是,
若要达到面试难度,那么要求就是遍历一遍链表,删除所有值为key的节点。
情况一:key连续,如下(1,2,3节点)

情况二:key不连续,如下(1,3节点)

代码实现:
public ListNode removeAllKey(int key){
if(this.head = null){
return null;
}
ListNode prev = this.head;
ListNode cur = this.head.next;
while(cur != null){
if(cur.val == key){
prev.next = cur.next;
cur = cur.next;
}else {
prev = cur;
cur = cur.next;
}
}
if(this.head.val == key){
this.head = this.head.next;
}
return this.head;
}
9.清空链表:public void clear()
1.简单粗暴的方法:将头节点置为空head = null;即可
2.细腻温柔的做法:将每一个节点都置为空
public void clear(){
while(this.head != null){
ListNode curNext = this.head.next;
this.head.next = null;
this.head = curNext;
}
}源码
import java.util.List;
//ListNode代表一个节点
class ListNode{
public int val;
public ListNode next;
//构造函数
public ListNode(int a){
this.val = a;
}
}
public class MyLinkedList {
public ListNode head;//链表的头
public void creatList() {
ListNode listNode1 = new ListNode(11);
ListNode listNode2 = new ListNode(22);
ListNode listNode3 = new ListNode(33);
ListNode listNode4 = new ListNode(44);
ListNode listNode5 = new ListNode(55);
this.head = listNode1;
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
listNode4.next = listNode5;
}
//头插法
public void addFirst(int data) {
ListNode node = new ListNode(data);
node.next = this.head;
this.head = node;
/*if(this.head == null){
this.head = node;
}else{
node.next = this.head;
this.head = node;
}*/
}
//尾插法
public void addLast(int data) {
ListNode node = new ListNode(data);
if (this.head == null) {
this.head = node;
} else {
ListNode cur = this.head;
while (cur.next != null) {
cur = cur.next;
}
cur.next = node;
}
}
//打印顺序表
public void display() {
ListNode cur = this.head;
while (cur != null) {
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
//查找是否包含关键字key是否在单链表当中
public boolean contains(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
}
//得到单链表的长度
public int Size() {
int count = 0;
ListNode cur = this.head;
while (cur != null) {
count++;
cur = cur.next;
}
return count;
}
//找到index位置的前一位置的地址
public ListNode findIndex(int index) {
ListNode cur = head.next;
while (index - 1 != 0) {
cur = cur.next;
index--;
}
return cur;
}
//任意位置插入,第一个数据节点为0号下标
public void addIndex(int index, int data) {
if (index < 0 || index > Size()) {
return;
}
if (index == 0) { //相当于头插法
addFirst(data);
return;
}
if (index == Size()) { //相当于尾插法
addLast(data);
return;
}
ListNode cur = findIndex(index);//找到index位置前一位置的地址
ListNode node = new ListNode(data);//初始化node
node.next = cur.next;
cur.next = node;
}
//找到key的前驱(前一节点)
public ListNode searchPrev(int key) {
ListNode cur = this.head;
while (cur.next != null) {
if (cur.next.val == key) {
return cur;
}
cur = cur.next;
}
return null;
}
//删除第一次出现关键字为key的节点
public void remove(int key) {
if (this.head == null) {
return;
}
if (this.head.val == key) {
this.head = this.head.next;
return;
}
ListNode cur = searchPrev(key);
if (cur == null) {
return; //没有要删除的节点
}
ListNode del = cur.next;//定义要删除的节点
cur.next = del.next;
}
//删除所有值为key的节点
public ListNode removeAllKey(int key) {
if (this.head = null) {
return null;
}
ListNode prev = this.head;
ListNode cur = this.head.next;
while (cur != null) {
if (cur.val == key) {
prev.next = cur.next;
cur = cur.next;
} else {
prev = cur;
cur = cur.next;
}
}
if (this.head.val == key) {
this.head = this.head.next;
}
return this.head;
}
//清空链表
public void clear() {
while (this.head != null) {
ListNode curNext = this.head.next;
this.head.next = null;
this.head = curNext;
}
}
}








 本文详细介绍了链表的概念、分类,以及如何通过代码实现单链表,包括节点创建、链表构建、节点插入、删除、查找和清空等操作。重点展示了头插法、尾插法和遍历链表的方法。
本文详细介绍了链表的概念、分类,以及如何通过代码实现单链表,包括节点创建、链表构建、节点插入、删除、查找和清空等操作。重点展示了头插法、尾插法和遍历链表的方法。

















 711
711

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










