对矩阵分解（MF）正则项的理解

最新推荐文章于 2023-05-25 16:06:05 发布

@刹那芳华逝

最新推荐文章于 2023-05-25 16:06:05 发布

阅读量270

点赞数

文章标签：推荐算法

本文链接：https://blog.csdn.net/m0_58071164/article/details/125934486

版权

推荐系统专栏收录该内容

3 篇文章 0 订阅

订阅专栏

在矩阵分解中，我们对得到的损失函数

$\sum_{p,q}^{}e_{pq}^{2}=\sum_{p,q}^{}(r_{pq}-\sum_{k=1}^{K}p_{ik}q_{kj})^{2}$

而在优化目标中，我们在损失函数后加上了正则项 $\lambda (\left \| p \right \|^{2}+\left \| q \right \|^{2})$ ，下面我们就对正则项系数 $\lambda$ 进行分析实验。

函数拟合分析

过拟合

过拟合表现为在训练集上测试较为准确而在测试集中测试准确度较低。一般会导致为损失函数值较大。因此，我们可以在所定义的损失函数后面加入一项永不为0的部分，那么最后经过不断优化损失函数还是会存在。其实这就是所谓的“正则化”。

欠拟合

欠拟合表现为在训练集正确度比较低，在测试集上测试正确度较低。而在实际中随着迭代次数的增大，基本不会出现欠拟合现象。

矩阵分解代码

# -*- coding: utf-8 -*-

from math import *
import  numpy as np
import matplotlib.pyplot as plt
#调用math、numpy、matplotlib库
 
def MF(R,P,Q,K,aplha,beta,steps):
    '''
    :param R: 用户-物品评分矩阵 m*n
    :param P: 用户的分解矩阵 m*k
    :param Q: 物品的分解矩阵 k*n
    :param K: 隐向量的维度
    :param aplha: 学习率
    :param beta: 正则化参数 
    '''
    print('开始分解原矩阵')
    Q=Q.T
    result=[]
    #开始训练  更新参数 计算损失值
    #更新参数 使用梯度下降方法
    print('开始训练')
    for step in range(steps):#训练次数
        ''''''
        for i in range(len(R)):
            for j in range(len(R[i])):
                eij=R[i][j]-np.dot(P[i,:],Q[:,j])#eij
                for k in range(K):#隐向量维度
                    if R[i][j]>0:
                        #梯度下降法更新参数
                        P[i][k]=P[i][k]+aplha*(2*eij*Q[k][j]-beta*P[i][k])
                        Q[k][j]=Q[k][j]+aplha*(2*eij*P[i][k]-beta*Q[k][j])
        eR=np.dot(P,Q)
        #计算损失值
        e=0
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j] > 0:
                    e = e + pow(R[i][j] - np.dot(P[i, :], Q[:, j]), 2)  # 损失函数求和
                    for k in range(K):
                        e = e + (beta / 2) * (pow(P[i][k], 2) + pow(Q[k][j], 2))  # 加入正则化后的损失函数求和
        result.append(e)
        if e < 0.001:
            break
    print('training Finshed 。。。。')
 
    return P, Q.T, result
 
 
if __name__ == '__main__':   #主函数
    R=[                 #原始矩阵
        [5,3,0,1],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,0,4],
        [0,1,5,4]
    ]#未进行评分用0表示
    R=np.array(R)
    N=len(R)    #原矩阵R的行数
    M=len(R[0]) #原矩阵R的列数
    K=3    #K值可根据需求改变
    P=np.random.rand(N,K) #随机生成一个 N行 K列的矩阵
    Q=np.random.rand(M,K) #随机生成一个 M行 K列的矩阵
    nP,nQ,result=MF(R,P,Q,K,aplha=0.0002,beta=0.02,steps=5000)
    print(result)
    print('原矩阵',R)         #输出原矩阵
    R_MF=np.dot(nP,nQ.T)
    print('计算出的矩阵',R_MF)      #输出新矩阵
    #画图
    plt.plot(range(len(result)),result)
    plt.xlabel("time")
    plt.ylabel("loss")
    plt.show()

改变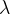 $\lambda$ 数值观察其对矩阵分解效果的影响

1、当 $\lambda =0.02$ 时，计算出的矩阵和误差-时间图如下所示：

2、当 $\lambda > 0.02$ 时，观察 $\lambda$ 从0.02逐渐增大到0.60时损失函数的数值变化，可以发现当 $\lambda=0.02$ 时，loss值最小且接近于0，当 $\lambda$ 增大到大于等于0.10时，误差已经接近8%附近，已经出现了过拟合现象，损失函数在多次迭代后值过大，如下图所示。