目录
目录
💥1 概述
准确估计电池的荷电状态(SOC)是电池管理系统(BMS)的基础。本文提出了一种考虑分数阶微积分的锂电池充电状态估计方法。首先,基于分数阶微积分理论建立了改进的二阶RC模型来模拟锂电池的特性。然后进行脉冲特性测试,获得电池端电压和电流,其中基于最小二乘法完成参数辨识。此外,将基于分数阶无气味卡尔曼滤波(分数阶无气味卡尔曼滤波)算法的方法应用于电池静态和动态放电实验中电池状态充电值的估计。
实验结果表明,该方法具有较高的电荷状态估计精度和效率,分数阶演算有助于电池的电荷状态估计。
基于FOMIAUKF(Fractional Order Multiple-Information Adaptive Unscented Kalman Filter)、分数阶模型、模型估计和多新息系数的SOC(State of Charge)估计是一种用于电池状态估计的研究方法。该方法结合了多种技术和算法,旨在提高对电池SOC的准确估计。
下面是基于FOMIAUKF、分数阶模型、模型估计和多新息系数的SOC估计的一般步骤:
1. 分数阶模型建立:将电池系统建模为分数阶动力学模型。分数阶微积分引入了非整数阶导数和积分的概念,可以更准确地描述电池的动态特性。
2. 模型参数估计:通过实验数据对电池模型的参数进行估计。这可以通过最小二乘法、最大似然估计或其它参数估计方法来实现。模型参数的准确估计对SOC估计的精度和稳定性非常重要。
3. FOMIAUKF算法设计:基于FOMIAUKF算法进行SOC估计。FOMIAUKF是一种基于非整数阶微积分和自适应无迹卡尔曼滤波的算法,可以克服传统卡尔曼滤波器中对系统非线性和不确定性的限制。
4. 多新息系数设计:为了提高SOC估计的精度和稳定性,采用多新息系数的策略。新息系数决定了滤波器更新和预测中历史信息的权重分配,合理选择和更新新息系数可以改善估计的性能。
5. 测量数据融合:将实际的电池测量数据与FOMIAUKF算法的估计结果进行融合。这可以包括电流、电压、温度等测量数据的采集和处理,以提高SOC估计的准确性。
6. 评估和优化:对SOC估计结果进行评估和优化。这可以包括与实际SOC值的比较、误差分析、误差补偿等,以及对估计算法和参数的调整和改进。
在电池管理系统中,准确估计电池的荷电状态(State of Charge, SOC)是至关重要的,因为它直接影响到电池的使用效率、安全性和寿命。近年来,随着分数阶理论、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)以及多新息理论的发展,这些技术被越来越多地应用于电池SOC的估计中。以下是一个基于分数阶模型(Fractional Order Model, FOM)、UKF以及多新息系数(Multiple Innovations)的电池SOC估计研究框架。
1. 分数阶模型(FOM)
分数阶模型相比传统的整数阶模型能更准确地描述电池系统的动态特性,因为它允许阶数(如电容、电阻等元件的阶数)为非整数。在电池SOC估计中,可以建立电池的分数阶等效电路模型,如分数阶RC网络模型。
步骤:
- 确定电池分数阶模型的阶数和参数。
- 使用实验数据或系统辨识方法(如最小二乘法、遗传算法等)来拟合模型参数。
2. 无迹卡尔曼滤波(UKF)
UKF是一种适用于非线性系统的状态估计算法,它通过无迹变换(Unscented Transformation, UT)来近似非线性函数的概率分布。在电池SOC估计中,UKF可以用来根据电池的电压、电流等测量值来更新SOC的估计值。
步骤:
- 设计UKF算法,包括选择状态变量(如SOC)、观测变量(如电压)和过程噪声、观测噪声的协方差矩阵。
- 在每个时间步,使用UT来生成Sigma点,并通过电池模型进行预测。
- 使用测量值更新Sigma点的权重,并计算新的状态估计和协方差矩阵。
3. 多新息理论
多新息理论通过利用多个时间点的观测信息来改进估计性能,特别是在处理具有时滞或噪声较大的系统时非常有效。在电池SOC估计中,可以引入多新息系数来优化UKF的更新过程。
步骤:
- 修改UKF的更新步骤,使其能够同时考虑多个时间点的观测信息。
- 设计多新息系数,这些系数可以根据系统的动态特性和观测噪声水平进行调整。
- 在每个时间步,使用多新息UKF算法来更新SOC的估计值。
4. 实验验证与性能评估
为了验证所提出方法的有效性,需要进行实验验证和性能评估。
步骤:
- 使用实际电池测试数据或模拟数据来测试所提出的方法。
- 比较基于FOMIAUKF(分数阶模型结合多新息UKF)的SOC估计结果与其他方法(如整数阶模型结合UKF、扩展卡尔曼滤波等)的估计结果。
- 评估估计精度、收敛速度、鲁棒性等性能指标。
5. 结论与展望
根据实验结果,总结FOMIAUKF在电池SOC估计中的优势和不足,并提出未来的研究方向和改进措施。
通过上述研究框架,可以系统地探索分数阶模型、UKF以及多新息理论在电池SOC估计中的应用,为提升电池管理系统的性能提供有力支持。
详细讲解见第4部分。
📚2 运行结果
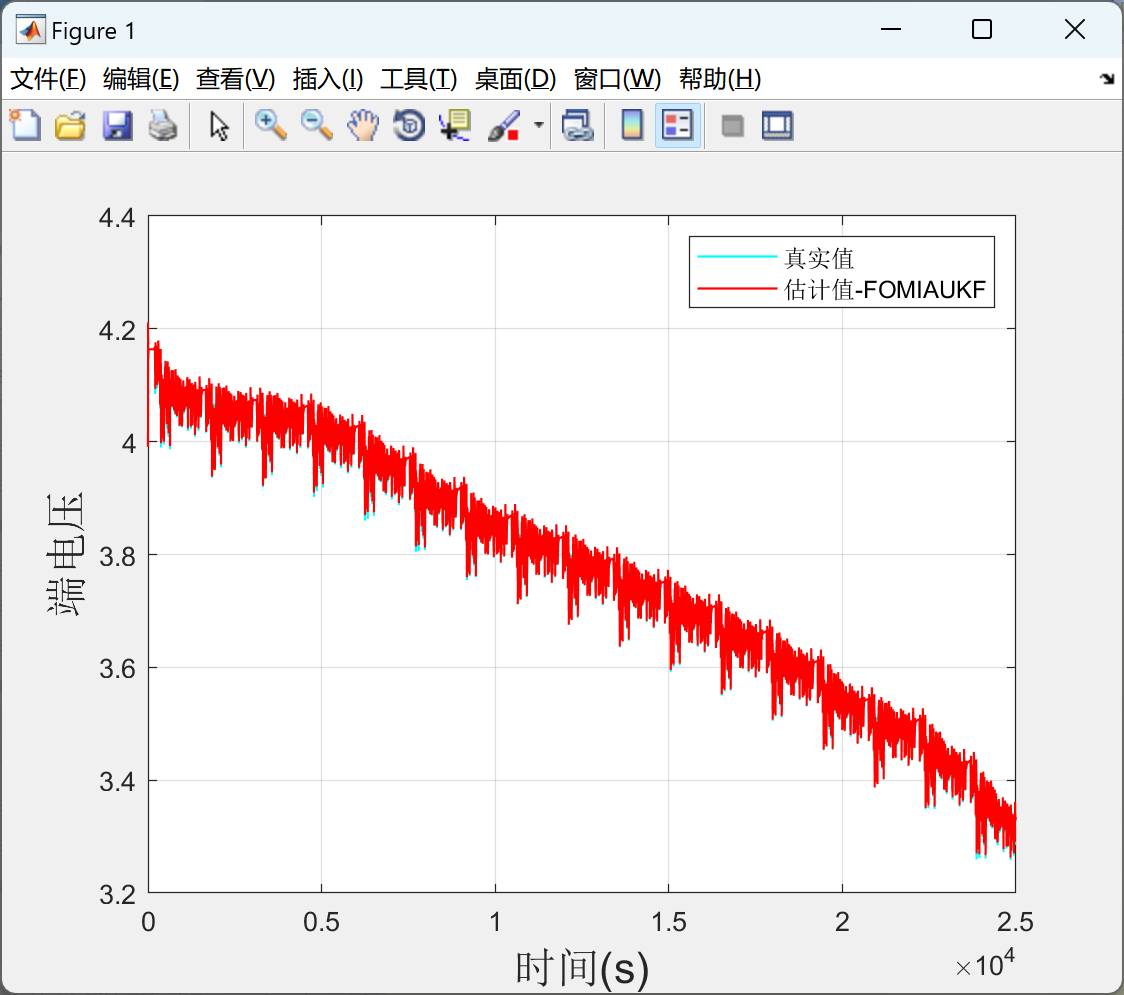



部分代码:
%% OCV-SOC
x=OCV_SOC(2,:);
y=OCV_SOC(1,:);
p=polyfit(x,y,8);
%% 分数阶模块中间变量
w_m=1; %因子
w_n=1; %因子
w=cell(1,T+1); %因子
w{1}=[1 0 0;0 1 0;0 0 0];
for j=2:T+1 %因子,参考说明文档及其参考文献
w_m=(1-(m+1)/(j-1))*w_m;
w_n=(1-(n+1)/(j-1))*w_n;
w{j}=[w_m 0 0;0 w_n 0;0 0 0];
end
%% 模型估计得到的电压值
Xekf=[0;0;0.8];%[U1,U2,SOC]初始值
L=length(Xekf);
Uoc(1)=p(1)*Xekf(3)^8+p(2)*Xekf(3)^7+p(3)*Xekf(3)^6+p(4)*Xekf(3)^5+p(5)*Xekf(3)^4+p(6)*Xekf(3)^3+p(7)*Xekf(3)^2+p(8)*Xekf(3)+p(9);%OCV
Vekf(1)=Uoc(1)+C*Xekf-Cur(1)*R0;%估计得到的端电压值
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。























 615
615

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








