应用时间序列案例-基于R语言

一.搜集数据

选取2019年3月到2022年3月的邮政业务总量当期值（月季度）如下：

x	y
1	1138.7
2	962.7
3	1252.9
4	1289
5	1381.4
6	1212.5
7	1190.5
8	1111.1
9	1089.1
10	1194
11	1132.4
12	1069.2
13	1141.9
14	694.6
15	1192.8
16	2300.3
17	2416.5
18	2044.7
19	1984.1
20	1809.8
21	1732.6
22	1843.5
23	1812.5
24	1633.4
25	1554.3
26	840
27	1712.3
28	1795.5
29	1473.1
30	1419.4
31	1349.2
32	1321.8
33	1369.1
34	1309.4
35	1245.6
36	1255.6

二.数据处理与分析

根据以上流程图开始分析（该图来自公众号“狗熊会”，我不允许还有统计学子没有关注他）

2.1平稳性检验

首先利用R语言画出时序图

library(readxl)
data <- read_excel("data.xlsx")
View(data)                                                                                
sh<-ts(data$y,start=data$x)
plot(sh)#sh为自定义名称

得到如下结果时序图

 是不是感觉它第一，没有周期性，第二没有趋势性，那是不是就是平稳序列了？nonono，差点就被骗了，因此我继续了对它进行单位根检验

library(tseries)#这个需要安装一下包，install.packages("tseries")
adf.test(data$y)

可以得到以下结果

 可以看到它的p值是远远大于0.05啊（哭泣

所以接下来将非平稳序列转化为平稳序列，采用2步一阶差分，参考R语言实现时间序列之8种平稳化方法_kh5lc的博客-CSDN博客_序列平稳化的方法

y1<-diff(data$y,2,1)
adf.test(y1)

得到如下结果

很叭戳！p值小于0.05，因此可以认为现在的数据是平稳序列了！

可以看看它的时序图

 看一下差分后的acf图

acf(y1)

可见样本自相关系数大部分都在2倍标准范围内

 2.2 白噪声检验

Box.test(y2,lag=3,type='L')#lag取值根据acf图决定

得到的结果如下：

 可见p值远小于0.05，因此可以认为差分后的序列为非白噪声序列

三.模型建立

3.1根据acf图和pacf图确定模型的阶数

acf图：

 pacf图：

 可以认为acf图是3阶拖尾，pacf是2阶拖尾，因此确定模型为ARIMA（2，1，3）

3.2 参数估计

model<-arima(y1,order=c(2,1,3),method="ML")
model

得到如下结果

 第一行输出的是参数估计值，第二行输出的是参数估计值的样本标准差

因此该ARIMA(2,1,3)的表达式为

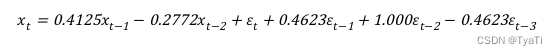
四.模型检验         

4.1 模型显著性检验

tsdiag(model)

得到如下结果：

 由最后一个图可以看出所有的点都在虚线上方，即所有Q统计量的p值均大于显著性水平0.05，此时可认为该模型显著成立。

五.模型预测

library("forecast")
fore<-forecast(model,h=10)#h为预测期数
plot(fore,lty=2)
lines(fore$fitted,col=4)#虚线为观察值，实线为拟合值

结果如下：