西电算法设计与分析课程复习笔记

m0_59467663

已于 2024-05-17 19:09:23 修改

阅读量1.4k

点赞数 37

文章标签：算法排序算法数据结构贪心算法动态规划深度优先

于 2024-05-15 19:53:19 首次发布

本文链接：https://blog.csdn.net/m0_59467663/article/details/138921229

版权

Design and Analysis of Algorithms Review

排序算法排序的过程、不同情况下时间复杂度、稳定性、是否原地排序
O、Ω、Θ表示法判断
主定理计算题
分治的三个步骤结合问题的描述
认识堆，建堆，调整堆的过程
动态规划的四个步骤，最优解，最优解的值等概念；动态转移方程，以及阐述含义；填写表格计算题；设计题
贪心的计算题
最短路径几种算法的原理、计算
回溯和npc的一些概念
几个经典问题属于哪类问题

Introduction(Ch1)

算法在软件开发中的位置
- 从体系结构到数据结构到算法
算法的定义
- 良定义的计算过程、解决特定问题的步骤、有输入和输出
为什么要分析性能
机器无关的时间分析

Getting Started(Ch2)

最大子数组问题
- 蛮力求解
循环不变式
- 初始化：循环开始前满足
- 保持：某次循环前成立，循环后也成立
- 终止：循环结束后仍成立
插入排序
- 非递归算法的分析方法
- RAM模型：无并发的顺序执行
  
  Best-case linear in $ O(n) $, worst-case quadratic in $ O(n^2) $
插入排序（Insertion Sort）是一种简单直观的排序算法，它的工作方式是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常使用in-place排序（即只需用到O(1)的额外空间的排序）

插入排序算法的步骤如下：
1. 从第一个元素开始，该元素可以认为已经被排序；
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置；
4. 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置；
5. 将新元素插入到该位置后；
6. 重复步骤 2~5。
分治/规模压缩策略的引入
分治的递归方法
- 分解：将原问题分解成若干个子问题，形式与原问题一致，但规模更小
- 解决：递归求解子问题，若子问题规模足够小，则停止递归，直接求解
- 合并：将子问题的解合并为原问题的解
分治算法是一种递归算法，可以多关注分解也可以多关合并。
分解时多做事：快速排序（Quick Sort）
快速排序是一种常见的排序算法，其基本思想是：
1. 分解：选取一个基准元素（pivot），将数组分成两个子数组，一个包含小于基准元素的元素，另一个包含大于或等于基准元素的元素。
2. 解决：对这两个子数组递归地进行快速排序。
3. 合并：因为子数组是就地排序的，所以不需要额外的合并步骤。
合并时多做事：归并排序（Merge Sort）
归并排序的步骤如下：
1. 分解：将待排序数组分解成两半，递归地分解直到每个子数组只有一个元素。
2. 解决：由于最小子数组只有一个元素，可以认为它已经排序好了。
3. 合并：将排好序的子数组合并成较大的有序数组，直到最后只有一个排序完毕的大数组。
二分应用于递归算法
- 归并排序
  分解：将$ n $个元素的序列分解成两个 $ n/2 $ 个元素的子序列
  解决：递归地排序两个子序列
  合并：归并两个有序的序列成为已经排好序的解
  合并的步骤
  1. 初始化：确定两个已排序的子数组的起始索引，通常这两个子数组是连续的，例如数组arr的左半部分arr[l…m]和右半部分arr[m+1…r]。
  2. 创建辅助数组：创建一个临时数组，其大小等于两个子数组的大小之和，用于存放合并后的已排序数组。
  3. 合并：使用两个指针，分别指向两个子数组的起始位置。比较两个指针所指向的元素，将较小的元素复制到临时数组中，并移动指针到下一个位置。重复这个过程，直到一个子数组的所有元素都被复制到临时数组中。
  4. 复制剩余元素：如果第二个子数组还有剩余的元素，将这些元素复制到临时数组的末尾。同样，如果第一个子数组有剩余的元素，也复制到临时数组的末尾。
  5. 复制回原数组：将临时数组中的所有元素复制回原数组的相应位置，此时原数组arr[l…r]就是已排序的。
    分析归并排序$ Θ(nlgn) $
- 递归树
- 代入法
- 数学推导
  数学归纳法（基本情况、归纳假设、目标证明）
Mathematical induction.
Powerful and general proof technique in discrete mathematics.
To prove a theorem true for all integers k≥0:
Base case: prove it to be true for n = 0;
Induction hypothesis: assuming it is true for arbitrary n
Induction step: show it is true for n+1
Claim: 0 + 1+ 2+3 + … + n = n(n + 1)/2 for all n≥0
Proof: (by mathematical induction)
Base case (n=0)
0 = 0(0+1)/2
Induction hypothesis: assume 0 + 1 + 2 + … + n = n(n+1) / 2
Induction step: 0 + 1 + 2 + … + n + n + 1 = n(n+1) / 2 + n + 1 = (n+1)(n+2)/2
- n推n-1应用于递归算法

Growth of Functions(Ch3)

O-notation
Ω-notation
Θ-notation

Recurrences(Ch4)

Substitution method 代入法
1. 猜测解的形式
2. 数学归纳法求解出常数（改变变量，残差等）
3. 证明解的正确性
Recursion-tree method 递归树法
$ T(n) = 3T(n/4) + Θ(n^2)$
Master method 主方法

Three common cases

Master theorem - examples

最大子数组的分治算法
分解：将A[low,high]分解成两个n/2规模的数组A[low,mid],A[mid+1,high]
解决：递归寻找两个子数组中的最大子数组
合并：选择子问题中的最大子数组和的序列

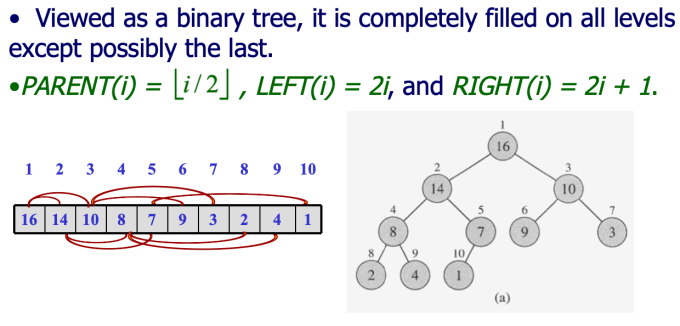
Heapsort (Ch5) (不稳定)

认识堆

The height of heap with n elements is lgn。
MAX-HEAPIFY ensures that a heap is max heap. O(log n)
BUILD-MAX-HEAP produces a max heap from an unordered array. Θ(n)

MAX-HEAPIFY

MAX-HEAPIFY 过程的描述：（自顶向下的）

输入：一个完全二叉树中的节点 i，以及一个数组 A 表示这个二叉树，其中 A[i] 是节点 i 的值，A[left(i)] 和 A[right(i)] 分别是节点 i 的左子节点和右子节点的值，且左右子树都是最大堆。
比较节点 i 与其子节点：比较 A[i] 与其子节点 A[left(i)] 和 A[right(i)] 的值。
交换：如果 A[i] 小于其子节点中的最大值，那么交换 A[i] 和那个较大的子节点的值。交换后，可能破坏了交换子节点的子树的堆性质。
递归：对交换后的子节点执行 MAX-HEAPIFY 过程，以确保该子节点以下的子树维持最大堆性质。
结束：当节点 i 的值大于或等于其子节点的值时，或者节点 i 已经是叶节点时，MAX-HEAPIFY 过程结束。

BUILD-MAX-HEAP（循环不变式证明正确性）
- 注意这里时间复杂度是O（n）
优先队列
Support the following basic operations.
- INSERT(S, x) （O(logn):自底向上的调整）
  inserts the element x into S
  第一步：堆末尾增加一个元素，堆规模增加一；
  第二步：重新调整为大顶堆。
- MAXIMUM(S) (常数时间)
  returns the element of S with the largest key
- EXTRACT-MAX(S) O（logn）
  removes and returns the element of S with the largest key
  第一步：移除堆顶元素；
  第二步：堆顶元素设为堆最后一个元素，堆规模减少一；
  第三步：重新调整为大顶堆。
- INCREASE-KEY(S, x, k) （O(logn):自底向上的调整）
  Increase the value of key of element x to the new value k.

Quicksort (Ch6) （不稳定）

快速排序的分治思想
- 分解：子数组A[p:r]根据枢轴(pivot)A[q]被分为比枢轴小的一侧(low side)A[p:q-1]和比枢轴大的一侧(high side)A[q+1:r]。
- 解决：通过递归调用快速排序实现对A[p:q-1]和A[q+1:r]的排序。
- 合并：因为子数组都是原地排序，此时A[p:r]有序。
快速排序的过程
快速排序的时间复杂度分析
- worse case：
  T(n) = T(n - 1) + T(0) + Θ(n)
  = T(n - 1) + Θ(1) + Θ(n)
  = T(n - 1) + Θ(n)
  = Θ(n^2)
- best case：T(n) = 2T(n/2) + Θ(n) = Θ(nlogn)
快速排序的随机化
- 将partition在序列中随机中随机抽样

Sorting in linear time (Ch7)

基于比较的排序算法的下界
- 最坏情况的下界(A lower bound for the worst case)
  从决策树根结点到可达叶结点的最长简单路径的长度（等于决策树的高度）代表最坏情况下的比较次数。
  最坏情况下，任何比较排序算法都需要Ω(n lg n)次比较。
  证明：设决策树高度为h，
  h ≥ lg (n!)
  ≥ lg (n/e)^n
  = n lg n - n lg e
  =Ω(n lg n)
Counting sort stable
Radix sort stable
Bucket sort

Sorting methods	Worst Case	Best Case	Average Case	Stable	Inplace	Application
Insert Sort	$n^2$	$n$	$n^2$	T	T	Very fast when n<50
Bubble Sort	$n^2$	$n$	$n^2$	T	T	Very fast when n<50
Merge Sort	$n l o g n$	$n l o g n$	$n l o g n$	T	F	Need extra space; good for external sort
Heap Sort	$n l o g n$	$n$	$n l o g n$	F	T	Good for real-time app
Quick Sort	$n^2$	$n l o g n$	$n l o g n$	F	T	Practical and fast
Counting Sort	$k + n$	$k + n$	$k + n$	T	F	Small, fixed range;
Radix Sort	$d (k + n)$	$d (k + n)$	$d (k + n)$	T	F	Fixed range
Bucket Sort	$n$	$n$	$n$	T	F	Uniform distribution

Medians and Order Statistics (Ch8)

基于随机算法的选择算法
运用到了划分数组算法，就是我们通常说的快速排序思想。由于该算法用到递归，需要的额外空间取决于递归栈的深度，平均情况下为T(n) = T(9n/10)+Θ(n)= Θ(n)，最坏情况下为T(n) = T(9n/10)+Θ(n)= Θ(n)

RANDOMIZED-SELECT(A, p, r, i)
 if p == r
     return A[p]  // 1 ≤ i ≤ r - p + 1 when p == r means that i = 1
 q = RANDOMIZED-PARTITION(A, p, r)
 k = q - p + 1
 if i == k
     return A[q]  // the pivot value is the answer
 elseif i < k
     return RANDOMIZED-SELECT(A, p, q - 1, i)
 else return RANDOMIZED-SELECT(A, q + 1, r, i - k)

Dynamic Programming(Ch9)

以下四步：
1. 描述最优解的结构特征。
2. 递归定义最优解的值。
3. 自下而上或备忘录计算最优解的值。
4. 根据计算信息构造最优解。
最优解和最优解的值
在动态规划问题中，最优解指的是在满足问题约束的条件下，使目标函数达到最优（最大或最小）的解。
最优解的值是指目标函数在这个最优解下达到的具体数值。
装配线调度问题
矩阵链乘 O(n^3)
最长公共子序列
最大子数组

Greedy Algorithms (Ch10)

贪心策略基本原理(Elements of the greedy strategy)
一般情况下，我们可以根据以下步骤设计贪心算法。

最优化问题为你做出选择后只有一个子问题需要求解。
证明每次做出贪心选择后，原问题总是有最优解，所以贪心选择总是安全的。
证明做出贪心选择后的子问题和贪心选择一起构成原问题的最优解，即原问题具有最优子结构。
能够用贪心算法求解的问题具有贪心选择性质和最优子结构。

贪心算法和动态规划的对比：
动态规划的选择依赖于子问题的解，所以一般采用自底向的方法求解问题。
贪心算法不依赖于子问题的解，所以一般采用自顶向下的方法求解问题。
使用贪心算法前，我们必须证明每个步骤做出贪心选择能生成全局最优解。
最优子结构(Optimal substructure)
最优子结构(optimal substructure)：如果一个问题的最优解包含其子问题的最优解，那么称该问题具有最优子结构。
贪心算法通常采用一个非常直接的方法运用最优子结构，假定通过对原问题的贪心选择就可以得到子问题，我们只需要证明做出贪心选择后的子问题和贪心选择一起构成原问题的最优解。该方法隐式地运用了归纳法，证明了每一步贪心选择都能构成原问题的最优解。
活动选择问题
贪活动结束时间
证明最优子结构的正确性：复制粘贴法
分数背包
贪性价比
0/1背包
哈夫曼编码

Shortest Paths （Ch11）

Dijkstra’s algorithm O（VlgV+E）
Dijkstra算法的实现为：从源点s开始进行广度优先搜索，通过从s点发出的所有边(s,v)将s的邻接顶点加入优先队列Q，并松弛所有从s发出的边。然后不断从优先队列Q中将距离s最近的顶点u出队，对u进行广度优先搜索，通过从s点发出的所有边(s,v)将s的邻接顶点加入优先队列，并松弛所有从 u 发出的边。直到Q为空，Dijkstra算法终止。

无负边权值的单源最短路径
Bellman-Ford algorithm
Dijkstra算法无法处理负权值的边，Bellman-Ford算法可以。其思想是遍历每个端点∣V−1∣次，每次对所有的边进行松弛操作。它还有一个优点,就是能处理负权环.因为我们是V-1次松弛操作.在这种情况下，保证能把这个图的最短路径求出来.第V次还有可以能松弛的,那说明就是负权环.
Floyd-Warshall algorithm
Floyd算法采用动态规划的思想
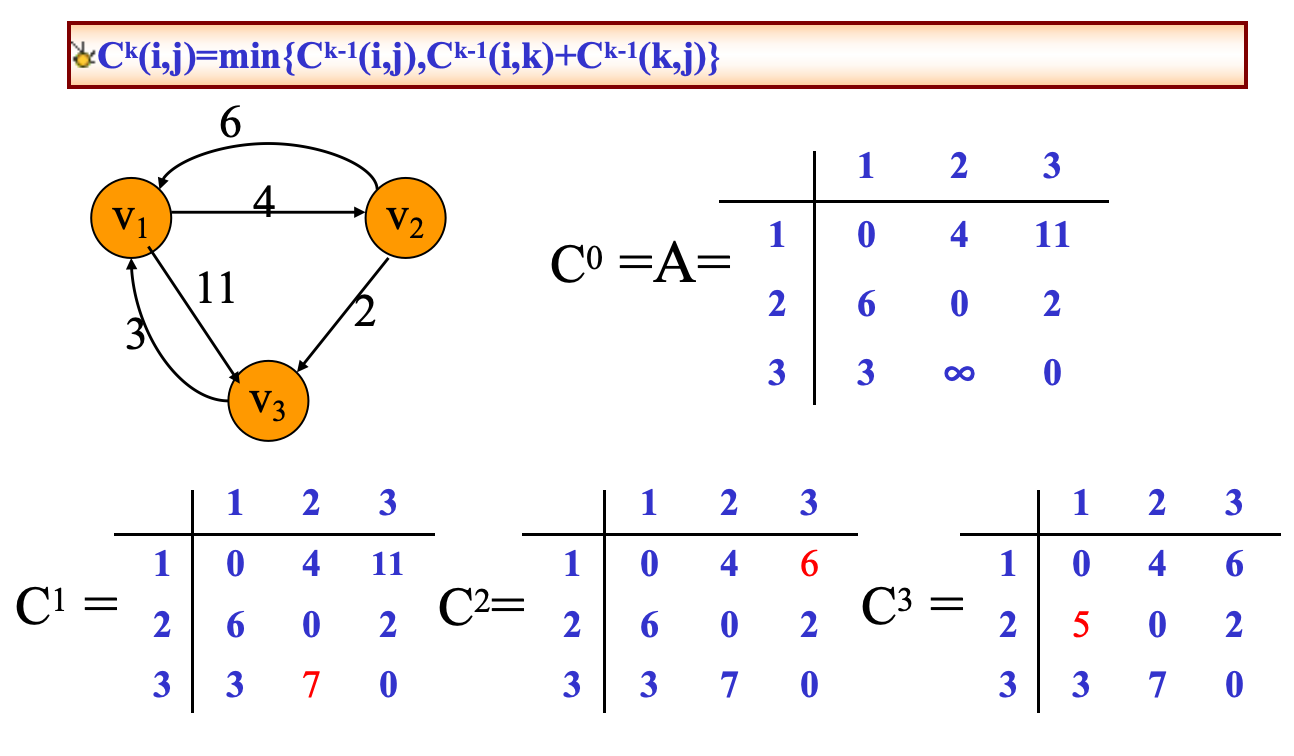
Johnson算法

Back-Tracking Algorithms （Ch12）

约束条件
分为显式约束和隐式约束
显式：规定了问题的解的分量的取值范围。如求n的全排列每个位置只能取1~n
隐式：用于判定候选解是否为可行解。如全排列的每个数字不允许重复。
问题状态和状态空间树
状态空间树是描述问题解空间的树形结构，每个结点称为一个问题状态。树的每条分支代表一次决策，从根结点到叶结点的路径就代表了一个候选解，称该叶结点所代表的状态为解状态。如果候选解是可行解则称之为答案状态。
剪枝函数
剪枝函数分为约束函数和限界函数
约束函数：避免无所谓的搜索那些已知不含答案状态的子树。
限界函数：用于最优化问题，剪去那些不可能含有最优答案结点的子树。
二者的区别在于：约束函数是对约束条件的实现，剪去不带答案结点的子树。而限界函数常用于求解最优化问题，它剪去的子树可能带答案结点，但不会是最优答案结点。
回溯法
回溯法是一种更为一般的解题方法。回溯法是通过搜索状态空间树来求问题的可行解或最优解的方法。本质就是dfs + 剪枝。
状态空间树的一些概念
- 活结点：没有生成全部儿子结点
- 死结点：儿子已经全部生成的结点，或已经剪枝无需向下扩展的结点
- E-结点：正在生成其儿子结点的活结点。
- 回溯法：当前E-结点一旦生成一个新的子结点，孩子就进入活结点表，且变成新的E结点
- 回溯法的基本思想是按照深度优先搜索的策略，从根节点出发深度搜索解空间树，当搜索到某一节点时，如果该节点可能包含问题的解，则继续向下搜索；反之回溯到其祖先节点，尝试其他路径搜索。
- 分支限界法：当前E-结点要生成其全部子结点到变为死结点，子结点进入活结点表，之后从活结点表中选择一个作为新的E-结点
- 分支限界法是利用广度优先搜索的策略或者以最小耗费(最大效益)优先的方式搜索问题的解空间树，对于解空间树中的活节点只有一次机会成为拓展节点，活节点一旦成为扩展节点，那么将一次性产生其所有儿子节点。
- 对于优先队列式的分支限界法，这些儿子节点中，不可行解或者一定不能成为最优解的儿子节点会被舍弃，其余儿子节点将会按照优先级依次存入一个活节点表(队列)，此后会挑出活节点表优先级最高的节点作为下次扩展节点，重复此过程，直至找到问题的最优解。

NP-Completeness （Ch13）

多项式时间 (Polynomial time)
我们通常认为多项式时间可解的问题是可处理的。原因有三：
经验表明，一旦某个问题的第一个多项式时间算法被发现后，就会出现更为高效的算法。
对于许多合理的计算模型，若一个问题在一个模型上多项式时间可解，则该问题在另一个模型上多项式时间可解。
由于多项式在加法、乘法和组合运算下是封闭的，因此多项式时间可解问题具有很好的封闭性。
不可判定问题
停机问题
NP 类是一个能够被多项式时间算法验证的语言类。
NP 表示非确定性多项式时间 (nondeterministic polynomial time)
NP-complete
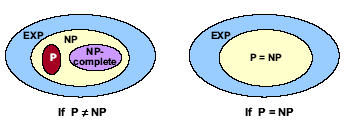
- 首先P问题是一类可以在多项式时间内求解的问题；
- NP问题是一类可以在多项式时间内验证解是否正确的问题；
- 显然， P⊆NP NP-Complete问题其实是一类特殊的NP问题，特殊之处在于所有的NP问题都可以多项式归约到NP-Complete问题上，即 NP≤pNP−Complete 换句话说就是，如果能够解决NP-Complete问题，就能解决所有的NP问题。
- 有6种NP-complete问题：
1. Packing problems: set-packing, independent set.
2. Covering problems: set-cover, vectex-cover.
3. Constraint satisfaction problems: SAT, 3-SAT.
4. Sequencing problems: hamiltonian-cycle, TSP.
5. Partitioning problems: 3D-matching,3-color.
6. Numerical problems: subset-sum, knapsack.