tensorflow零基础入门学习

import tensorflow as tf
a=tf.constant([1,5],dtype=tf.int64)#创建一个一阶张量，里面有两个元素 1和5，且类型：64为整型
print(a)#直接打印 a 的所有信息
print(a.dtype)#打印 a 的类型
print(a.shape)#打印 a 的形状

输出

注意事项：

（1）shape里面 ’，‘隔开几个数字，这个张量就是几维的.本例隔开一个数字，所以阶数是1（2）shape里面的数字代表元素个数。本例有两个元素1，5

输出格式转换

默认输出格式为 numpy，可以通过转换为 Tensor格式

输入

import tensorflow as tf
import numpy as np
a=np.arange(0,5)
b=tf.convert_to_tensor(a,dtype=tf.int64)
print(a)
print(b)

输出

创建固定数

tf.zeros()输出类型为 float32

a1=tf.zeros(2)#创建1维度，2个元素全为0的张量
a2=tf.zeros([2,3])#创建2维度，3个元素全为0的张量

tf.ones()输出类型为 float32

b1=tf.ones(4)#创建1维度，4个元素全为1的张量
b2=tf.ones([3,2])#创建3维度，2个元素全为1的张量

tf.fill(x,y)输出类型为 int32

c1=tf.fill(3,2)#创建1维，3个元素全为2的张量
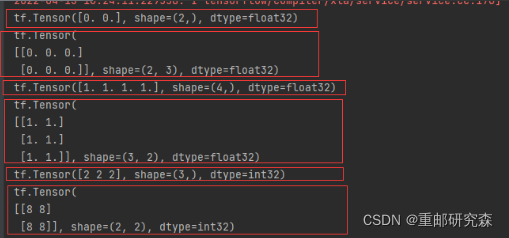
c2=tf.fill([2,2],8)#创建2维，2个元素全为8的张量

输入

import tensorflow as tf
a1=tf.zeros(2)#创建1维度，2个元素全为0的张量
a2=tf.zeros([2,3])#创建2维度，3个元素全为0的张量
b1=tf.ones(4)#创建1维度，4个元素全为1的张量
b2=tf.ones([3,2])#创建3维度，2个元素全为1的张量
c1=tf.fill(3,2)#创建1维，3个元素全为2的张量
c2=tf.fill([2,2],8)#创建2维，2个元素全为8的张量

print(a1)
print(a2)
print(b1)
print(b2)
print(c1)
print(c2)

输出

创建正态分布随机数

tf.random.normal([维度,个数],mean=均值,stddev=标准差)   正态分布随机数

tf.random.truncated_normal([维度,个数],mean=均值,stddev=标准差)截断式正态分布随机数。并且数据取值在（均值+-两倍标准差）

标准差公式：

输入

import tensorflow as tf

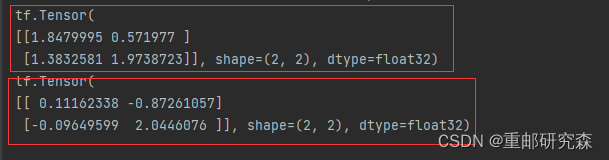
a=tf.random.normal([2,2],mean=0.5,stddev=1)

b=tf.random.truncated_normal([2,2],mean=0.5,stddev=1)

print(a)

print(b)

输出

创建均匀分布随机数

tf.random.uniform（【维度，个数】，minval=最小值，maxval=最大值）

输入

import tensorflow as tf

a=tf.random.uniform([2,3],minval=0,maxval=2)

print(a)

输出

入门函数

1.cast（）

tf.cast（）

强制tensor转换为该数据类型

语法：tf.cast（张量名，dtype=数据类型）

2.reduce_min（）

tf.reduce_min()

计算张量维度上元素最小值

语法：tf.reduce_min(张量名)

3.reduce_max（）

tf.reduce_max()

计算张量维度上元素最大值

语法：tf.reduce_max(张量名)

输入

import tensorflow as tf

a=tf.constant([1,2,3])

b=tf.cast(a,tf.float64)


c=tf.reduce_min(b)
d=tf.reduce_max(b)
print(a)
print(b)
print(c)
print(d)

输出

4.axis（）

实现计算的时候选择指定行，或者列。默认是计算所有元素

axis=1。代表行计算

axis=0。代表列计算

输入

import tensorflow as tf

x=tf.constant([1,2,3],[3,4,5])


a=tf.reduce_mean(x)
b=tf.reduce_sum(x,axis=1)#1+2+3
c=tf.reduce_sum(x,axis=0)#3+4+5
print(x)
print(a)
print(b)

输出

5.Variable（）

将变量标记为“可训练”。被标记的信息会在反向传播中记录梯度信息。

输入

import tensorflow as tf

tf.Variable("初始值")
w=tf.Variable(tf.random_normal([2,2,],mean=0,stddev=1))

输出

6.四则运算

加法：tf.add()

减法：tf.subtract()

乘法：tf.multiply()

除法：tf.divide()

注意事项：四则运算的张量必须维度相同

输入

import  tensorflow as tf

a=tf.ones([1,3])#3个1
b=tf.fill([1,3],3)#3个3
print(a)
print(b)
print(tf.add(a,b))
print(tf.subtract(a,b))
print(tf.multiply(a,b))
print(tf.divide(a,b))

输出

7.平方，次方，开方

平方：tf.square()

次方：tf.pow()

开方：tf.sqrt()

输入

import tensorflow as tf

a=tf.fill([1,2],3.)

print(a)

print(tf.pow(a,3))#a的三次方
print(tf.square(a))
print(tf.sqrt(a))

输出

8.矩阵乘

tf.matmul()

输入

import  tensorflow as tf

a=tf.ones([3,2])#3*2
b=tf.fill([2,3],2.)#2*3

print(tf.matmul(a,b))#3*3

输出

9.from_tensor_slices()

将特征和标签进行配对

注意事项：numpy和tensor格式都满足该函数

输入

import tensorflow as tf

features=tf.constant([12,23,10,17])
labels=tf.constant([0,1,1,0])
dataset=tf.data.Dataset.from_tensor_slices((features,labels))

print(dataset)

for element in dataset:
    print(element)

输出

10.GradientTape（）

实现某个函数对指定参数求导

输入

import tensorflow as tf

with tf.GradientTape() as tape:
    w=tf.Variable(tf.constant(3.0))
    loss=tf.pow(w,2)
grad=tape.gradient(loss,w)#w的平方求导为 2w。然后2*3=6
print(grad)

输出

11.enumrate（）

遍历每个元素（列表，元组，字符串）。方式为索引 + 元素

输入

import tensorflow as tf

seq=["one","two","three"]#列表

for i,element in enumerate(seq):
    print(i,element)

输出

12.one_hot（）

独热编码。常用于 “是非问题”。1：表示是。0表示：非

输入

import tensorflow as tf

classes=3
labels=tf.constant([1,0,2])
output=tf.one_hot(labels,depth=classes)

print(output)

输出

结果分析：第一次索引的下标从0开始递增。这时标签为0的数据为“是”，其他便签为“非”。所以第二个数为 1.其他数为0.第2次索引的下标为1。这时标签为1的数据为“是”，其他便签为“非”。所以第1个数为 1.其他数为0.

13.nn.softmax（）

使输出结果的概率之和满足：所有概率相加=1

输入

import tensorflow as tf

y=tf.constant([1.01,2.01,-0.66])

y_pro=tf.nn.softmax(y)

print("Afer softmax,y_pro is : ",y_pro)

输出

14.assign_sub（）

实现更新参值并且返回新值。

注意事项：该函数调用的参数必须为：Variable类型（可训练）。其中assign_sub（x），x代表自减x

输入

import  tensorflow as tf

w=tf.Variable(4)

w.assign_sub(2)#4-2=2

print(w)

输出

15.argmax（）

返回张量沿指定维度最大值的“索引”。其中axis=0代表列，aixs=1代表行

输入

import  tensorflow as tf
import numpy as np

test=np.array([[1,2,3],[2,3,4],[5,4,3],[8,7,2]])
print(test)

print(tf.argmax(test,axis=0))#列值最大的索引
print(tf.argmax(test,axis=1))#行值最大的索引

输出

第一个训练模型 -狗尾巴花

狗尾巴花数据读写

从 sklearn 包 datasets 读取数据

输入

from sklearn import datasets

from pandas import  DataFrame

import pandas as pd

x_data=datasets.load_iris().data#data返回iris数据集里面所有输入特征
y_data=datasets.load_iris().target#target返回iris数据集里面所有标签

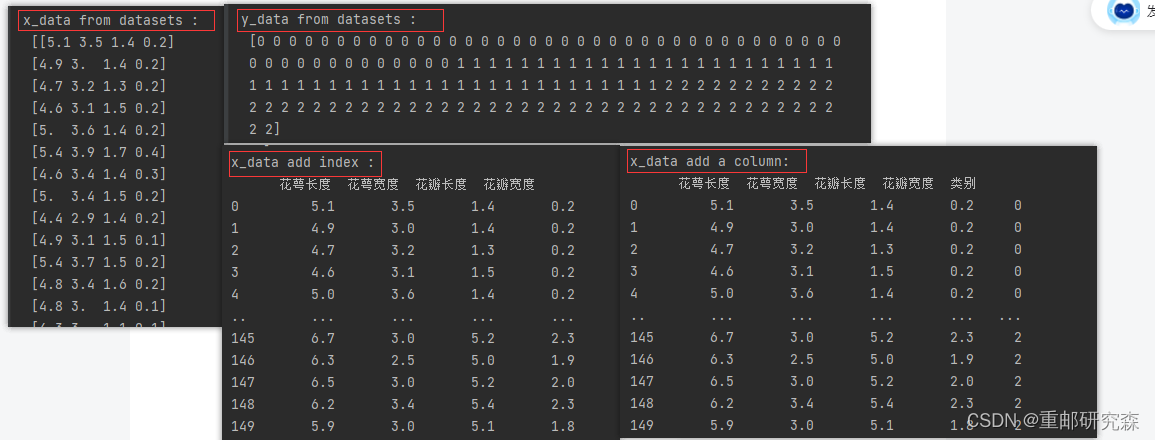
print("x_data from datasets : \n",x_data)
print("y_data from datasets : \n",y_data)

x_data=DataFrame(x_data,columns=['花萼长度','花萼宽度','花瓣长度','花瓣宽度'])#把数据变为表格形式，并且每一列加标签
pd.set_option('display.unicode.east_asian_width',True)#设置列名字对齐
print("x_data add index : \n",x_data)

x_data['类别']=y_data#新加一列，列标签为‘类别’

print("x_data add a column: \n",x_data)

输出

神经网络实现狗尾巴花分类

1.准备数据

1.数据集读入

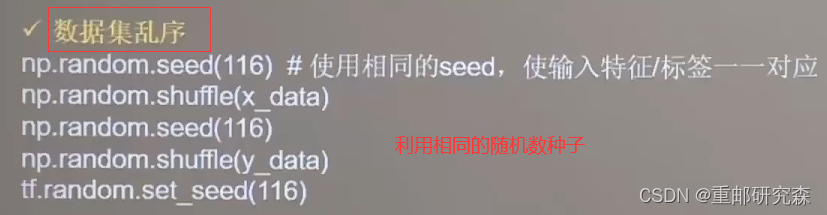
2.数据集乱序

3.生成“训练集”和“测试集”

4.输入特征和标签配对

2.搭建神经网络

定义神经网络中所有可训练参数

3.参数优化

嵌套循环迭代，with结构更新参数，显示当前loss

4.测试效果

计算当前参数前向传播后的准确率，显示当前acc（准确率）

5.acc / loss可视化

画出曲线

输入

# -*- coding: UTF-8 -*-
# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np

# 导入数据，分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同，stddev=标准差（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

# 训练部分
for epoch in range(epoch):  #数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  #batch级别的循环 ，每个step循环一个batch
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

        # 实现梯度更新 w1 = w1 - lr * w1_grad    b = b - lr * b_grad
        w1.assign_sub(lr * grads[0])  # 参数w1自更新
        b1.assign_sub(lr * grads[1])  # 参数b自更新

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all/4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

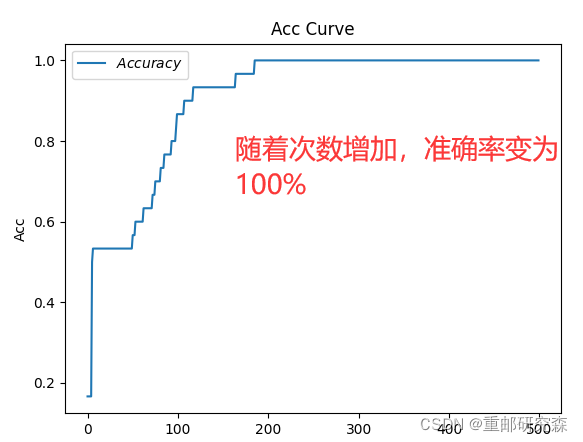
# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()

输出

基础知识

基础函数

1.where（）

进行比较判断，类似C语言的双目运算符

语法：where（条件，真值返回，假值返回）

输入

import tensorflow as tf

a=tf.constant([1,2,3,1,1])

b=tf.constant([0,1,3,4,5])

c=tf.where(tf.greater(a,b),a,b)#if a>b 则c=a，否则 c=b

print(c)

输出

2.random.RandomState.rand()

返回一个随机数【0，1）

输入

import numpy as np

rdm = np.random.RandomState(seed=1)
a = rdm.rand()
b = rdm.rand(2, 3)
print("a:", a)
print("b:", b)

输出

3.vstack（）

实现数组按垂直方向叠加。比如1维+1维=2维

语法：vstack（（数组1，数组2））

输入

import numpy as np

a=np.array([1,2,3])
b=np.array([4,5,6])
c=np.vstack((a,b))
print(c)

输出

4.mgrid_ravel_c

mgrid：实现生成一个多维矩阵。

语法：mgrid【起始值：结束值：步长，起始值：结束值：步长。。。】

ravel：把数组变为一维数组

c_：返回间隔数值配对

输入

import numpy as np

x,y=np.mgrid[1:3:1,2:5:0.5]

grid=np.c_[x.ravel(),y.ravel()]

print(x)
print(y)
print(grid)

输出

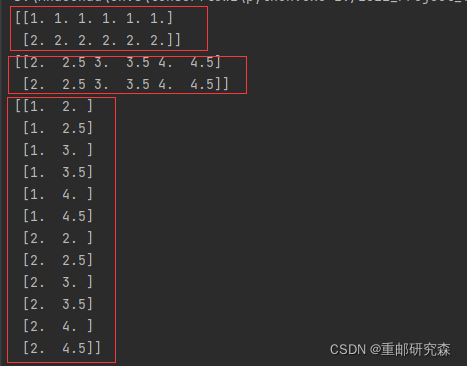
解释：由于现在是两个进行结合，所以按照（2-5）且步长0.5算，也就是2，2.5，3，3.5，4，4.5一共6个数

神经网络复杂度

不包括输入层

空间复杂度

层数=隐藏层的层数 + 1个输出层

总参数=总w+总b

例如上图中：3*4+4 + 4*2+2 = 26 第一层+第二层

时间复杂度

例如上图中：3*4 + 4*2 = 20 第一层+第二层

学习率

lr：代表每次参数更新的快慢幅度

举例：

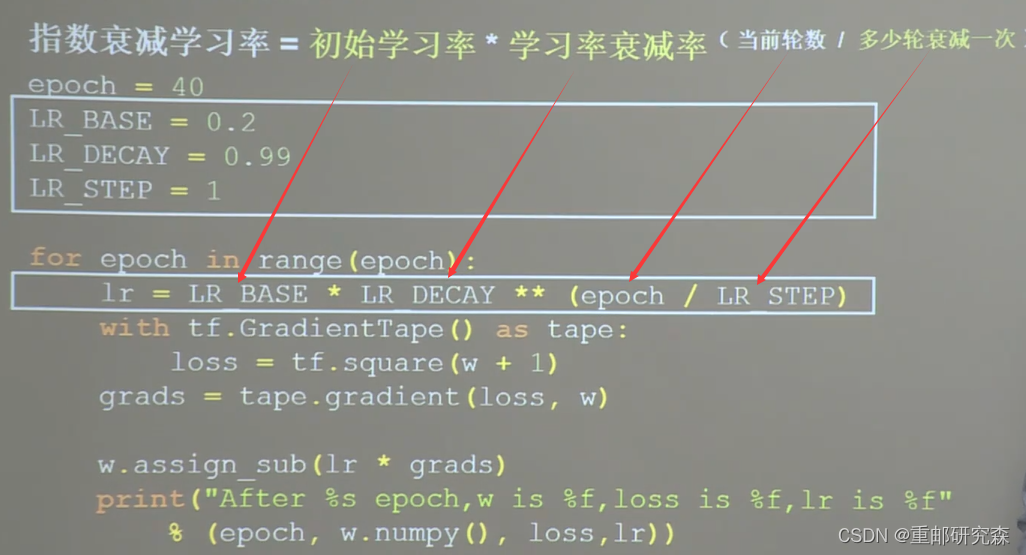
指数衰减学习率

原理：先用较大的学习率，快速得到优化解，然后逐步减小学习率

公式：初始学习率 * 学习衰减率^(当前轮数/多少轮衰减一次)

举例：

激活函数

Sigmoid函数

特点：（1）容易造成梯度消失（因为求导结果在【0-0.25】）

（2）输出非0均值，收敛慢

（3）幂运算复杂，训练时间长

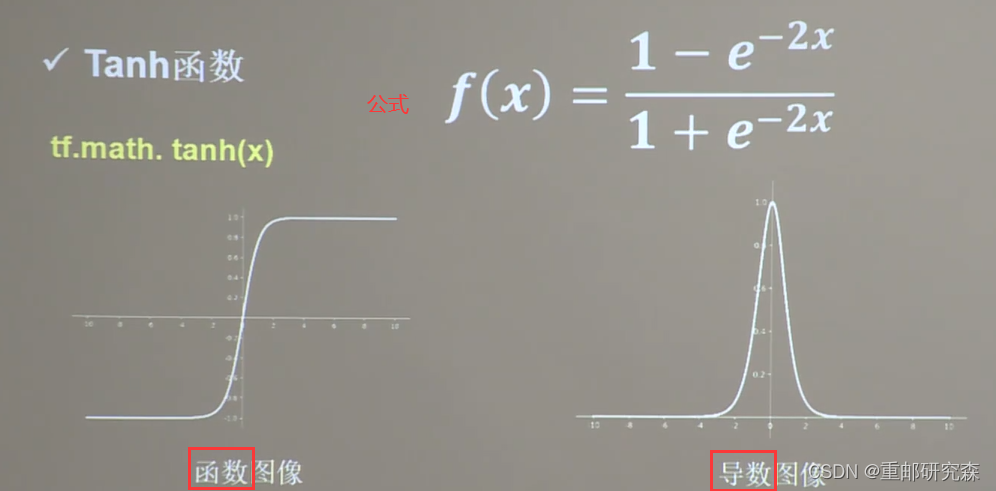
Tanh函数

特点：（1）输出是0均值

（2）容易造成梯度消失

（3）幂运算复杂，训练时间长

Relu函数

优点：

（1）解决了梯度消失问题（在正区间内）

（2）只需要判断输入是否大于0，计算速度快

（3）收敛速度快于 sigmod 和 tanh

缺点：

（1）输出非0均值，收敛慢

（2）对于负数部分，某些神经元不会被激活

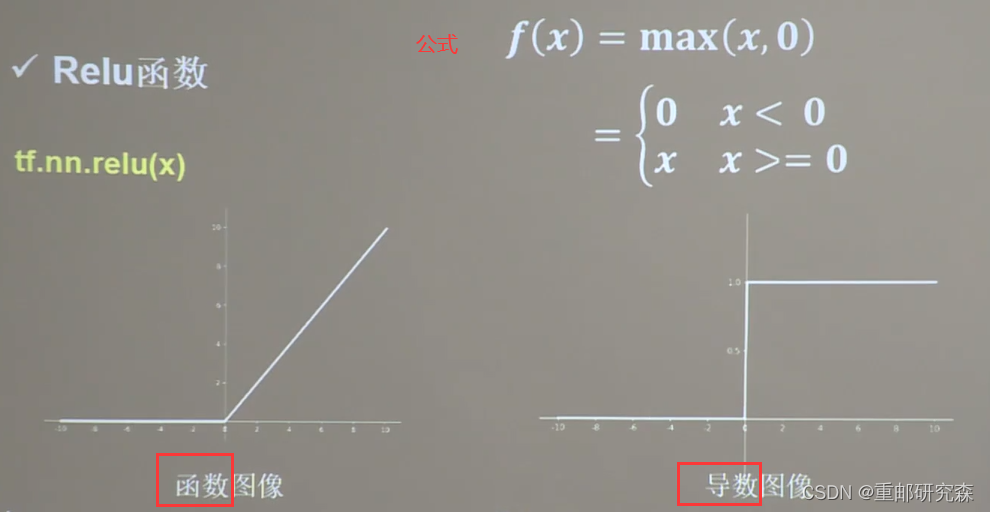
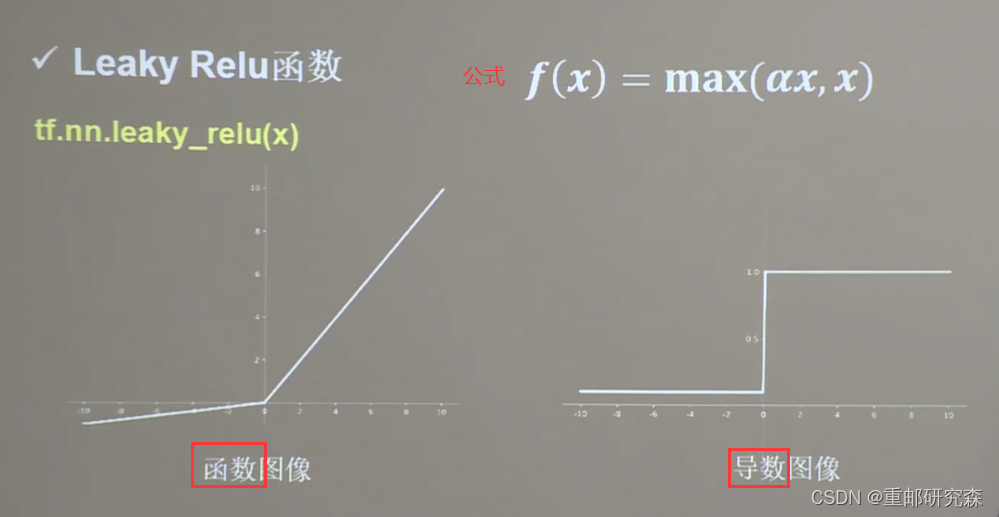
Leaky Relu函数

理论上比 Relu函数好，但是实际却没有

激活函数总结

损失函数

定义：损失函数是预测值和答案的差距

主流计算方式：均方误差，自定义，交叉熵

均方误差

import tensorflow as tf
import numpy as np

SEED = 23455#用来保证每次生成的随机数一样

rdm=np.random.RandomState(seed=SEED)
x=rdm.rand(32,2)#生成32行*2列特征值
y_=[[x1+x2+(rdm.rand()/10-0.05)]for (x1,x2) in x]#(rdm.rand()/10-0.05)=【-0.05-+0.05】
x=tf.cast(x,dtype=tf.float32)#改变类型

w1=tf.Variable(tf.random.normal([2,1],stddev=1,seed=1))

epoch=15000#迭代次数
lr=0.002#学习率

for epoch in range(epoch):
    with tf.GradientTape() as tape:
        y=tf.matmul(x,w1)#矩阵乘法
        loss_mse=tf.reduce_mean(tf.square(y_ - y))#按均方误差求解，reduce_mean求平均值
    grads=tape.gradient(loss_mse,w1)
    w1.assign_sub(lr * grads)

    if epoch % 500 == 0:
        print("After %d tarining steps ,w1 is " % (epoch))
        print(w1.numpy(),"\n")
print("Final w1 is: ",w1.numpy())#按numpy格式输出w1

自定义损失函数

import tensorflow as tf
import numpy as np

SEED = 23455
#调整COST和PROFIT的值可以控制预测
COST = 1
PROFIT = 99

rdm=np.random.RandomState(seed=SEED)
x=rdm.rand(16,2)#生成32行*2列特征值
y_=[[x1+x2+(rdm.rand()/10-0.05)]for (x1,x2) in x]#(rdm.rand()/10-0.05)=【-0.05-+0.05】
x=tf.cast(x,dtype=tf.float32)#改变类型

w1=tf.Variable(tf.random.normal([2,1],stddev=1,seed=1))

epoch=10000
lr=0.002

for epoch in range(epoch):
    with tf.GradientTape() as tape:
        y=tf.matmul(x,w1)
        loss=tf.reduce_sum(tf.where(tf.greater(y,y_),(y-y_)*COST,(y_ - y)*PROFIT))

    grads=tape.gradient(loss,w1)
    w1.assign_sub(lr*grads)

    if epoch % 500 == 0:
        print("After %d tarining steps ,w1 is " % (epoch))
        print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())  # 按numpy格式输出w1

# 自定义损失函数
# 酸奶成本1元， 酸奶利润99元
# 成本很低，利润很高，人们希望多预测些，生成模型系数大于1，往多了预测

交叉熵

用来表示求出的值于答案接近情况，也就是越大的话，预测越准确

import tensorflow as tf

loss_1=tf.losses.categorical_crossentropy([1,0],[0.6,0.4])
loss_2=tf.losses.categorical_crossentropy([1,0],[0.8,0.2])

print("loss_1: ",loss_1)
print("loss_2: ",loss_2)
if loss_1> loss_2 :
        print("loss1更接近")
else :
    print("loss2更接近")

softmax和交叉熵

输出先经过softmax符合概率分布，再把这个 y 和答案y 计算交叉熵损失函数

import tensorflow as tf
import numpy as np

y_=np.array([[1,0,0],[0,1,0],[0,0,1],[1,0,0],[0,1,0]])
y=np.array([[12,3,2],[3,10,1],[1,2,5],[4,6.5,1.2],[3,6,1]])

y_pro=tf.nn.softmax(y)

loss_1=tf.losses.categorical_crossentropy(y_,y_pro)
loss_2=tf.nn.softmax_cross_entropy_with_logits(y_,y)

print("分布结果： ",loss_1)
print("合并结果： ",loss_2)

拟合

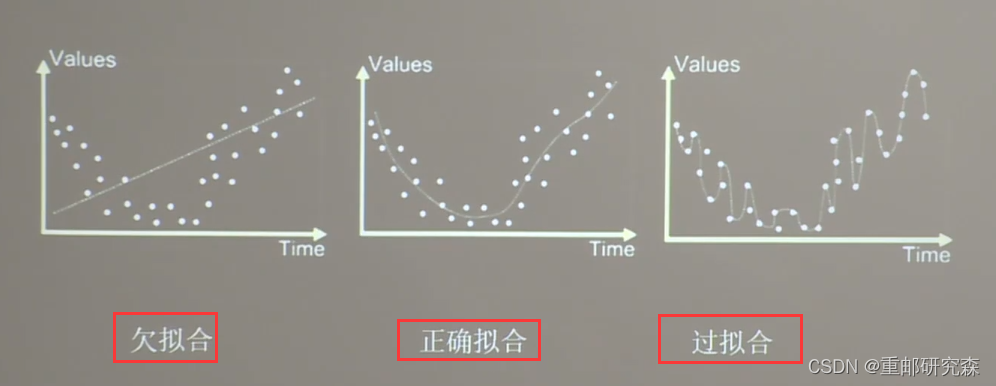
欠拟合

问题：学习的不够彻底

解决办法：（1）增加输入特征项

（2）增加网络参数

（3）减少正则化参数

过拟合

问题：学习的太彻底，但对新数据没用

解决办法：（1）数据清洗

（2）增大训练集

（3）增大正则化参数

正则化缓解过拟合

原理：正则化再损失函数中引入模型复杂度指标，利用w加权值，弱化噪声

公式：

其中，loss（w）的算法有两个，如下：

# 导入所需模块
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd

# 读入数据/标签 生成x_train y_train
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])

x_train = x_data
y_train = y_data.reshape(-1, 1)

Y_c = [['red' if y else 'blue'] for y in y_train]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)

# from_tensor_slices函数切分传入的张量的第一个维度，生成相应的数据集，使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)

# 生成神经网络的参数，输入层为4个神经元，隐藏层为32个神经元，2层隐藏层，输出层为3个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))

w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))

lr = 0.005  # 学习率为
epoch = 800  # 循环轮数

# 训练部分
for epoch in range(epoch):
    for step, (x_train, y_train) in enumerate(train_db):
        with tf.GradientTape() as tape:  # 记录梯度信息

            h1 = tf.matmul(x_train, w1) + b1  # 记录神经网络乘加运算
            h1 = tf.nn.relu(h1)
            y = tf.matmul(h1, w2) + b2

            # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_mse = tf.reduce_mean(tf.square(y_train - y))
            # 添加l2正则化
            loss_regularization = []
            # tf.nn.l2_loss(w)=sum(w ** 2) / 2
            loss_regularization.append(tf.nn.l2_loss(w1))
            loss_regularization.append(tf.nn.l2_loss(w2))
            # 求和
            # 例：x=tf.constant(([1,1,1],[1,1,1]))
            #   tf.reduce_sum(x)
            # >>>6
            loss_regularization = tf.reduce_sum(loss_regularization)
            loss = loss_mse + 0.03 * loss_regularization  # REGULARIZER = 0.03

        # 计算loss对各个参数的梯度
        variables = [w1, b1, w2, b2]
        grads = tape.gradient(loss, variables)

        # 实现梯度更新
        # w1 = w1 - lr * w1_grad
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])
        w2.assign_sub(lr * grads[2])
        b2.assign_sub(lr * grads[3])

    # 每200个epoch，打印loss信息
    if epoch % 20 == 0:
        print('epoch:', epoch, 'loss:', float(loss))

# 预测部分
print("*******predict*******")
# xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx, yy拉直，并合并配对为二维张量，生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络，进行预测，probs为输出
probs = []
for x_predict in grid:
    # 使用训练好的参数进行预测
    h1 = tf.matmul([x_predict], w1) + b1
    h1 = tf.nn.relu(h1)
    y = tf.matmul(h1, w2) + b2  # y为预测结果
    probs.append(y)

# 取第0列给x1，取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
plt.scatter(x1, x2, color=np.squeeze(Y_c))
# 把坐标xx yy和对应的值probs放入contour函数，给probs值为0.5的所有点上色  plt.show()后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()

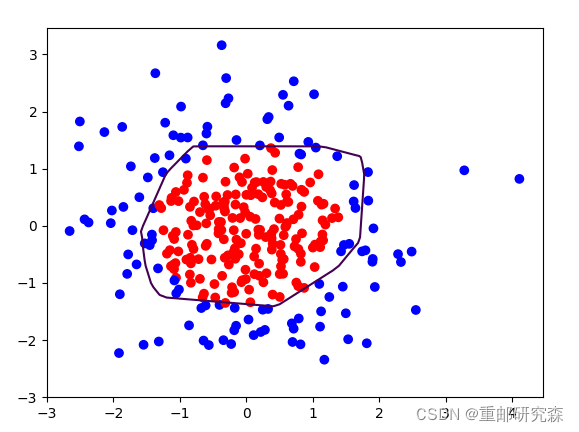
# 读入红蓝点，画出分割线，包含正则化
# 不清楚的数据，建议print出来查看

结果：

优化器

定义：引导神经网络更新参数的工具

实现步骤

SGD （无m）随机梯度下降

代码实现

        # 实现梯度更新 w1 = w1 - lr * w1_grad    b = b - lr * b_grad
        w1.assign_sub(lr * grads[0])  # 参数w1自更新
        b1.assign_sub(lr * grads[1])  # 参数b自更新

SGDM （有M的SGD）随机梯度下降

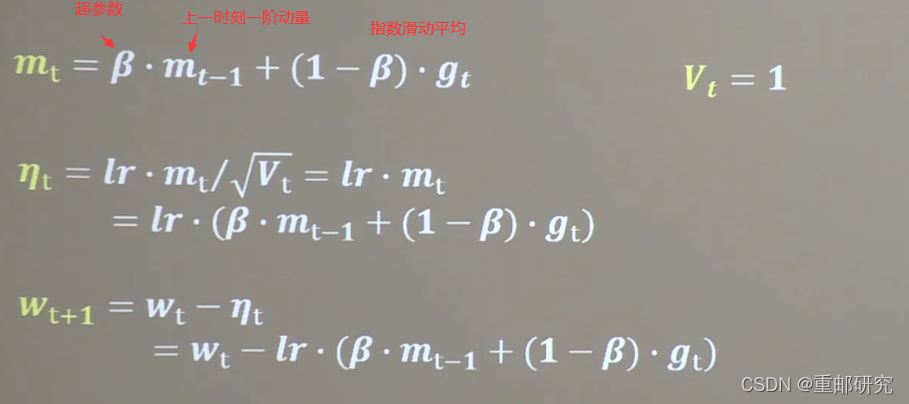
代码实现

# sgd-momentun  beta是超参数=0.9
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)

Adagrad（SGD上加入二阶动量）

代码实现

# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))

RMSProp

代码实现

# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))

Adam

代码实现

 # adam
        m_w = beta1 * m_w + (1 - beta1) * grads[0]
        m_b = beta1 * m_b + (1 - beta1) * grads[1]
        v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
        v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])

        m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
        m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
        v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
        v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))

        w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
        b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))

keras搭建网络八股

搭建网络八股keras.sequential

sequential用于上层输出，下层输入，不适用于下次还带输入的模型

keras.sequential搭建网络八股方法

六步法：

1->import

2->train test（指定训练集的输入特征和标签）

3->model=tf.keras.model.Sequential（搭建网络结构，逐层描述网络）

4->model.compile（选择哪种优化器，损失函数）

5->model.fit（执行训练过程，输入训练集和测试集的特征+标签，batch，迭代次数）

6->model.summary（打印网络结构和参数统计）

第三步使用方法

第四步使用方法

第五步使用方法

keras.sequential搭建网络八股狗尾巴花

import tensorflow as tf
from sklearn import datasets
import numpy as np

x_train = datasets.load_iris().data
y_train = datasets.load_iris().target

np.random.seed(116)
np.random.shuffle(x_train)
np.random.seed(116)
np.random.shuffle(y_train)
tf.random.set_seed(116)
#输出层为3，所以是3
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(3, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())
])

model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

model.fit(x_train, y_train, batch_size=32, epochs=500, validation_split=0.2, validation_freq=20)

model.summary()

搭建网络八股keras.class

第三步和sequential不一样！

keras.class搭建网络八股方法

六步法：

1->import

2->train test（指定训练集的输入特征和标签）

3->class MyModel(model) model=Mymodel（搭建网络结构，逐层描述网络）

4->model.compile（选择哪种优化器，损失函数）

5->model.fit（执行训练过程，输入训练集和测试集的特征+标签，batch，迭代次数）

6->model.summary（打印网络结构和参数统计）

keras.class搭建网络八股狗尾巴花

import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras import Model
from sklearn import datasets
import numpy as np

x_train = datasets.load_iris().data
y_train = datasets.load_iris().target

np.random.seed(116)
np.random.shuffle(x_train)
np.random.seed(116)
np.random.shuffle(y_train)
tf.random.set_seed(116)

class IrisModel(Model):
    def __init__(self):
        super(IrisModel, self).__init__()
        self.d1 = Dense(3, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())

    def call(self, x):
        y = self.d1(x)
        return y

model = IrisModel()

model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

model.fit(x_train, y_train, batch_size=32, epochs=500, validation_split=0.2, validation_freq=20)
model.summary()

MNIST数据集

里面有很多手写数字，0-9，因此利用这个图像数据集进行优化

注意事项：1.图像数据集需要拉直操作

搭建MNIST数据集keras.sequential

这里和上面区别在于：

第二步：

1.数据集别人已经分好，不需要自己设置训练集和测试集大小

第三步：

2.图像数据需要拉直（model里面第三步）

3.这里有两层，一个隐藏层，输出层

第四步：

4.优化器为adam

第五步：

没有利用分隔函数，而是直接写入测试集

import tensorflow as tf

mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0

model = tf.keras.models.Sequential([
    #图像数据需要拉直
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

model.fit(x_train, y_train, batch_size=32, epochs=5, validation_data=(x_test, y_test), validation_freq=1)
model.summary()

搭建MNIST数据集keras.class

import tensorflow as tf
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras import Model

mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0


class MnistModel(Model):
    def __init__(self):
        super(MnistModel, self).__init__()
        self.flatten = Flatten()
        self.d1 = Dense(128, activation='relu')
        self.d2 = Dense(10, activation='softmax')

    def call(self, x):
        x = self.flatten(x)
        x = self.d1(x)
        y = self.d2(x)
        return y


model = MnistModel()

model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

model.fit(x_train, y_train, batch_size=32, epochs=5, validation_data=(x_test, y_test), validation_freq=1)
model.summary()

fashion数据集

搭建fashion数据集keras.sequential

import tensorflow as tf
fashion=tf.keras.datasets.fashion_mnist
(x_train,y_train),(x_test,y_test)=fashion.load_data()
x_train,x_test=x_train/255.0,x_test/255.0

model=tf.keras.models.Sequential([
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128,activation='relu'),
    tf.keras.layers.Dense(10,activation='softmax')
])

model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy']
              )

model.fit(x_train,y_train,batch_size=32,epochs=5,validation_data=(x_test,y_test),validation_freq=1)

model.summary()

搭建fashion数据集keras.class

import tensorflow as tf
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras import Model

fashion = tf.keras.datasets.fashion_mnist
(x_train, y_train),(x_test, y_test) = fashion.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0


class MnistModel(Model):
    def __init__(self):
        super(MnistModel, self).__init__()
        self.flatten = Flatten()
        self.d1 = Dense(128, activation='relu')
        self.d2 = Dense(10, activation='softmax')

    def call(self, x):
        x = self.flatten(x)
        x = self.d1(x)
        y = self.d2(x)
        return y


model = MnistModel()

model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

model.fit(x_train, y_train, batch_size=32, epochs=5, validation_data=(x_test, y_test), validation_freq=1)
model.summary()

神经网络八股扩展

自建数据集解决本领域应用

通过自建的数据集进行训练。

import tensorflow as tf
from PIL import Image
import numpy as np
import os

train_path = './mnist_image_label/mnist_train_jpg_60000/'
train_txt = './mnist_image_label/mnist_train_jpg_60000.txt'
x_train_savepath = './mnist_image_label/mnist_x_train.npy'
y_train_savepath = './mnist_image_label/mnist_y_train.npy'

test_path = './mnist_image_label/mnist_test_jpg_10000/'
test_txt = './mnist_image_label/mnist_test_jpg_10000.txt'
x_test_savepath = './mnist_image_label/mnist_x_test.npy'
y_test_savepath = './mnist_image_label/mnist_y_test.npy'


def generateds(path, txt):
    f = open(txt, 'r')  # 以只读形式打开txt文件
    contents = f.readlines()  # 读取文件中所有行
    f.close()  # 关闭txt文件
    x, y_ = [], []  # 建立空列表
    for content in contents:  # 逐行取出
        value = content.split()  # 以空格分开，图片路径为value[0] , 标签为value[1] , 存入列表
        img_path = path + value[0]  # 拼出图片路径和文件名
        img = Image.open(img_path)  # 读入图片
        img = np.array(img.convert('L'))  # 图片变为8位宽灰度值的np.array格式
        img = img / 255.  # 数据归一化 （实现预处理）
        x.append(img)  # 归一化后的数据，贴到列表x
        y_.append(value[1])  # 标签贴到列表y_
        print('loading : ' + content)  # 打印状态提示

    x = np.array(x)  # 变为np.array格式
    y_ = np.array(y_)  # 变为np.array格式
    y_ = y_.astype(np.int64)  # 变为64位整型
    return x, y_  # 返回输入特征x，返回标签y_


if os.path.exists(x_train_savepath) and os.path.exists(y_train_savepath) and os.path.exists(
        x_test_savepath) and os.path.exists(y_test_savepath):
    print('-------------Load Datasets-----------------')
    x_train_save = np.load(x_train_savepath)
    y_train = np.load(y_train_savepath)
    x_test_save = np.load(x_test_savepath)
    y_test = np.load(y_test_savepath)
    x_train = np.reshape(x_train_save, (len(x_train_save), 28, 28))
    x_test = np.reshape(x_test_save, (len(x_test_save), 28, 28))
else:
    print('-------------Generate Datasets-----------------')
    x_train, y_train = generateds(train_path, train_txt)
    x_test, y_test = generateds(test_path, test_txt)

    print('-------------Save Datasets-----------------')
    x_train_save = np.reshape(x_train, (len(x_train), -1))
    x_test_save = np.reshape(x_test, (len(x_test), -1))
    np.save(x_train_savepath, x_train_save)
    np.save(y_train_savepath, y_train)
    np.save(x_test_savepath, x_test_save)
    np.save(y_test_savepath, y_test)

model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

model.fit(x_train, y_train, batch_size=32, epochs=5, validation_data=(x_test, y_test), validation_freq=1)
model.summary()

其中重点部分如下：

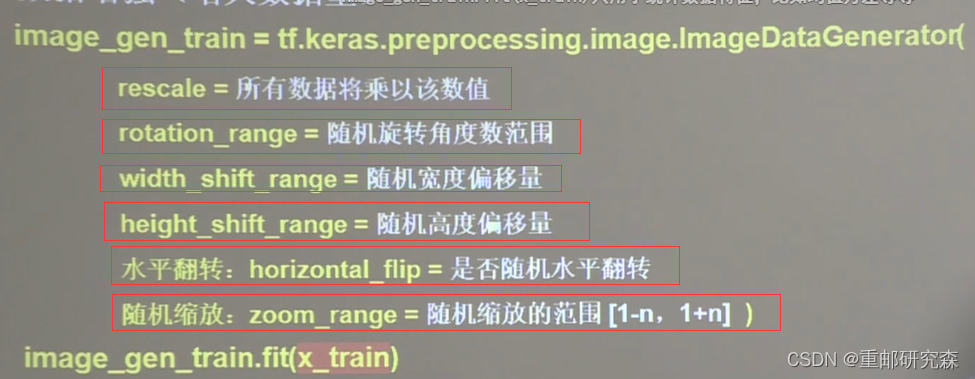
数据增强，扩充数据集

对数据集中的图片进行增强处理

# 显示原始图像和增强后的图像
import tensorflow as tf
from matplotlib import pyplot as plt
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import numpy as np

mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)

image_gen_train = ImageDataGenerator(
    rescale=1. / 255,
    rotation_range=45,
    width_shift_range=.15,
    height_shift_range=.15,
    horizontal_flip=False,
    zoom_range=0.5
)
image_gen_train.fit(x_train)
print("xtrain",x_train.shape)
x_train_subset1 = np.squeeze(x_train[:12])
print("xtrain_subset1",x_train_subset1.shape)
print("xtrain",x_train.shape)
x_train_subset2 = x_train[:12]  # 一次显示12张图片
print("xtrain_subset2",x_train_subset2.shape)

fig = plt.figure(figsize=(20, 2))
plt.set_cmap('gray')
# 显示原始图片
for i in range(0, len(x_train_subset1)):
    ax = fig.add_subplot(1, 12, i + 1)
    ax.imshow(x_train_subset1[i])
fig.suptitle('Subset of Original Training Images', fontsize=20)
plt.show()

# 显示增强后的图片
fig = plt.figure(figsize=(20, 2))
for x_batch in image_gen_train.flow(x_train_subset2, batch_size=12, shuffle=False):
    for i in range(0, 12):
        ax = fig.add_subplot(1, 12, i + 1)
        ax.imshow(np.squeeze(x_batch[i]))
    fig.suptitle('Augmented Images', fontsize=20)
    plt.show()
    break;

断点续讯，存取模型

调用已经存在的模型来进行训练

参数提取，把参数存入文本

返回模型中可训练的参数

acc/loss可视化，查看训练效果

查看acc和loss图像

应用程序，给图识物

预测数据

卷积神经网络基础概念

这里要明确，卷积是为了提取特征，把提取的特征再送入到之前的全连接层进行训练

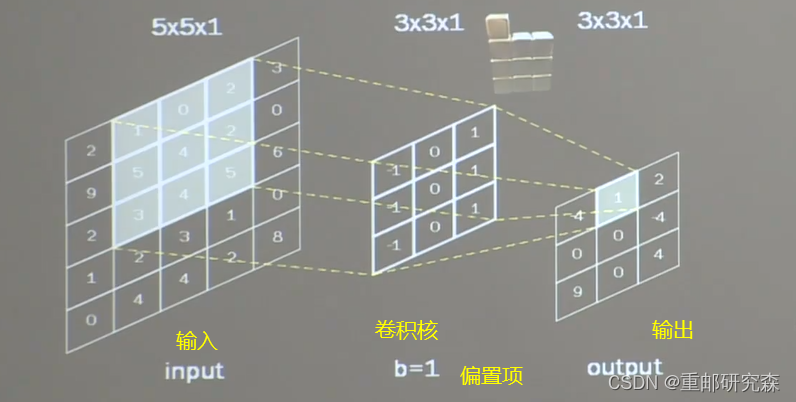
卷积

一般利用一个正方形（体）的卷积核，指定了宽，高以及移动步长在输入特征图上进行滑动，从而遍历输入特征的每个像素点，每移动一次，卷积核与对应区域重合部分相乘加上偏置项求和得到一个输出特征的像素点。

黑白图片：单通道，3*3*1的卷积核

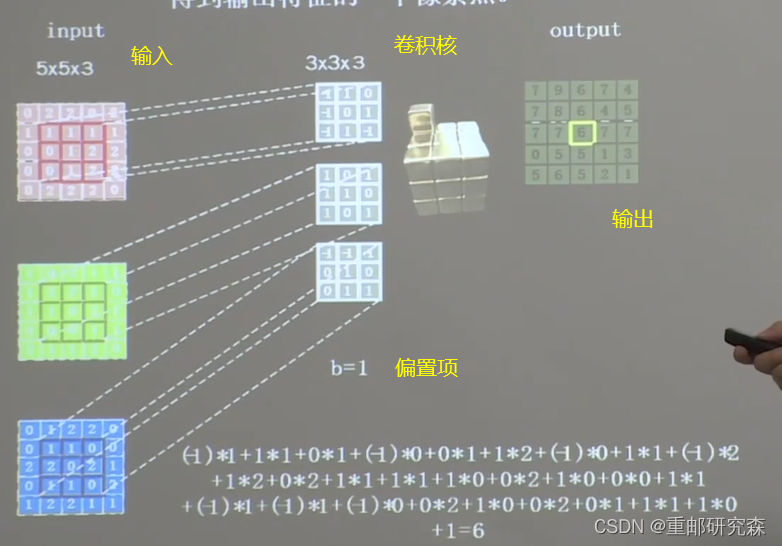
彩色图片：多通道，3*3*5的卷积核

输入特征的通道数：决定了卷积核的深度（第三个值）

当前层卷积核的个数：决定了输出特征图的个数

感受野

定义：卷积神经网络各输出特征图中的每个像素点，在原始输入图片上映射区域的大小

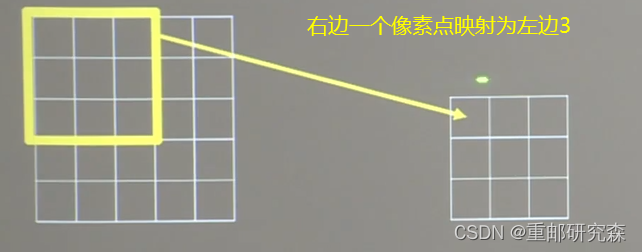
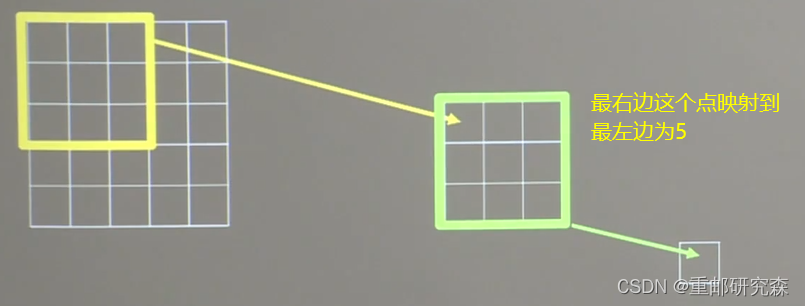
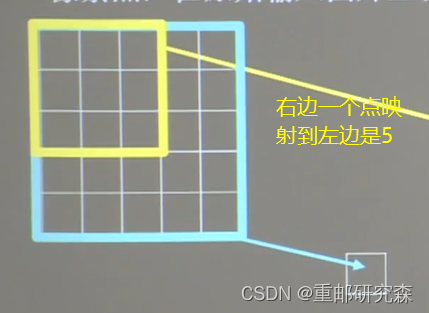
针对输出像素点感受野的不同，其也不同，计算过程如下：

两层3*3

一层5*5

全零填充

定义：在输入特征图上填充为0的区域

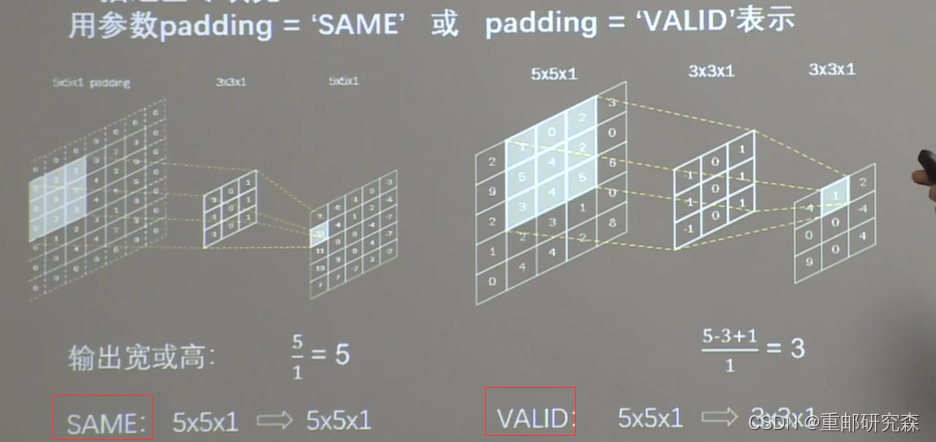
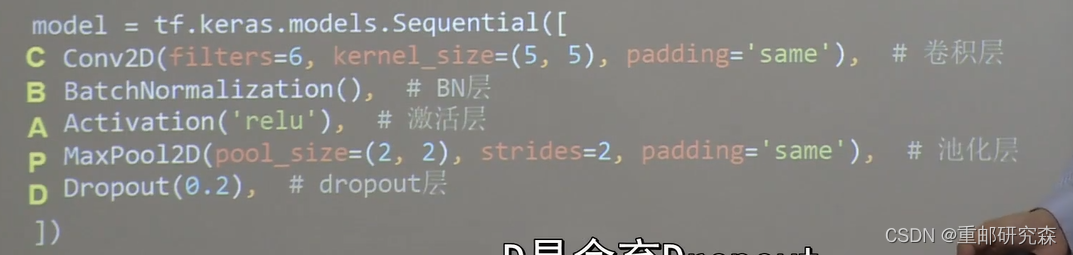
TF描述卷积层

Conv2D(filters=6, kernel_size=(5, 5), padding='same')  # 卷积层

批标准化（BN）

标准化：使数据符合0均值，1为标准差的分布

BN：对一个 batch 做标准化处理

加入缩放因子和偏移因子是为了防止过拟合

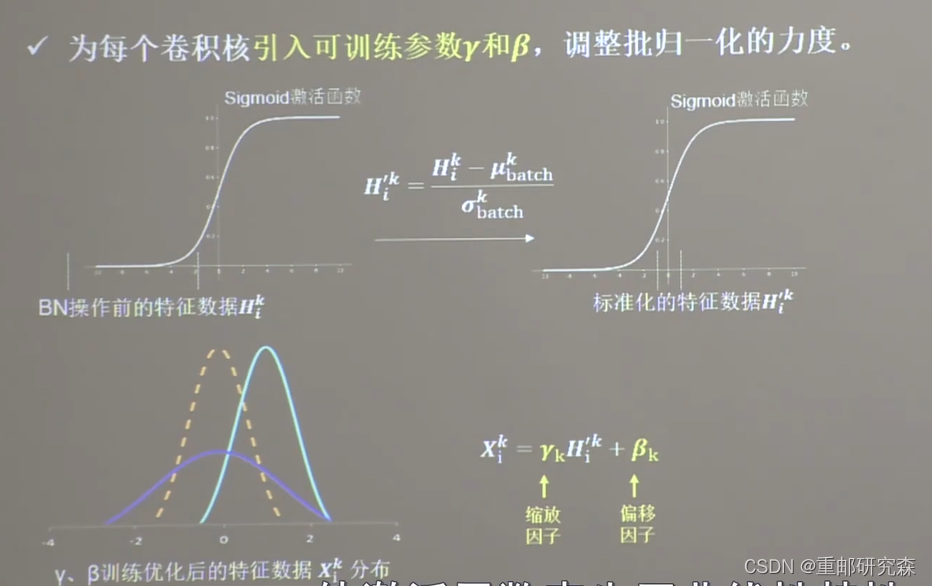
BN层的位置

TF 描述BN层

 self.b1 = BatchNormalization()  # BN层

池化

定义：用于减少卷积神经网络中特征数据量

方法：最大池化（提取图片纹理），均值池化（保留背景特征）

TF描述池化

 self.p1 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')  # 池化层

舍弃

为了缓解过拟合，在神经网络训练时，舍弃一部分神经元，等到使用时再恢复链接

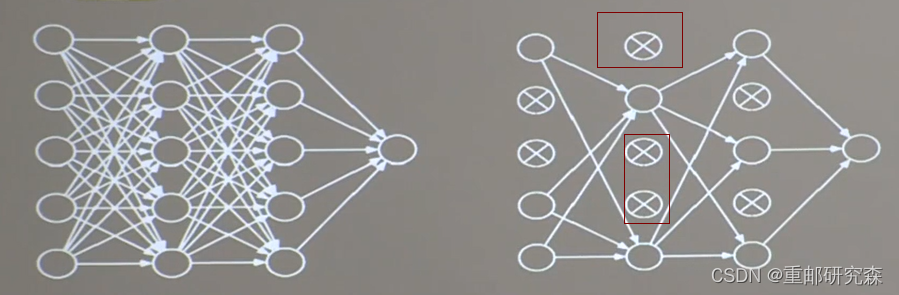
TF描述舍弃

 self.d1 = Dropout(0.2)  # dropout层

卷积神经网络小结

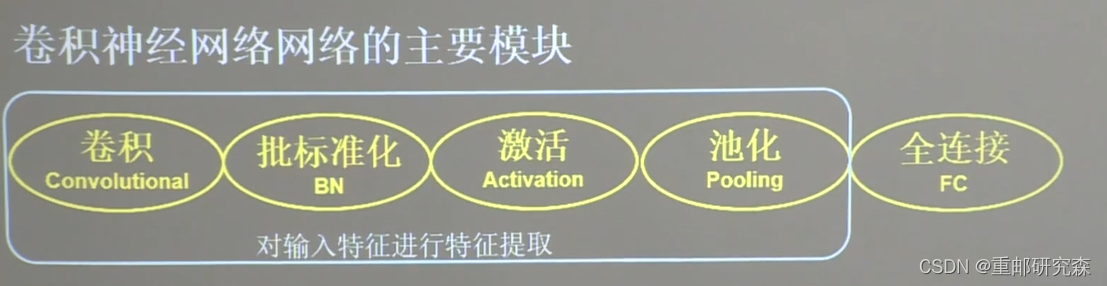
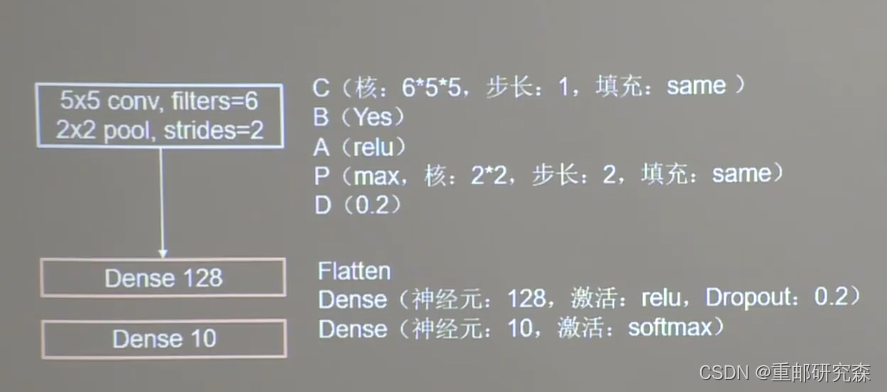
class Baseline(Model):
    def __init__(self):
        super(Baseline, self).__init__()
        self.c1 = Conv2D(filters=6, kernel_size=(5, 5), padding='same')  # 卷积层
        self.b1 = BatchNormalization()  # BN层
        self.a1 = Activation('relu')  # 激活层
        self.p1 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')  # 池化层
        self.d1 = Dropout(0.2)  # dropout层

        self.flatten = Flatten()
        self.f1 = Dense(128, activation='relu')
        self.d2 = Dropout(0.2)
        self.f2 = Dense(10, activation='softmax')

    def call(self, x):
        x = self.c1(x)
        x = self.b1(x)
        x = self.a1(x)
        x = self.p1(x)
        x = self.d1(x)

        x = self.flatten(x)
        x = self.f1(x)
        x = self.d2(x)
        y = self.f2(x)
        return y

CIFAR10数据集

提供5万张32*32像素点的十分类彩色图片和标签

提供1万张32*32像素点的十分类彩色图片和标签

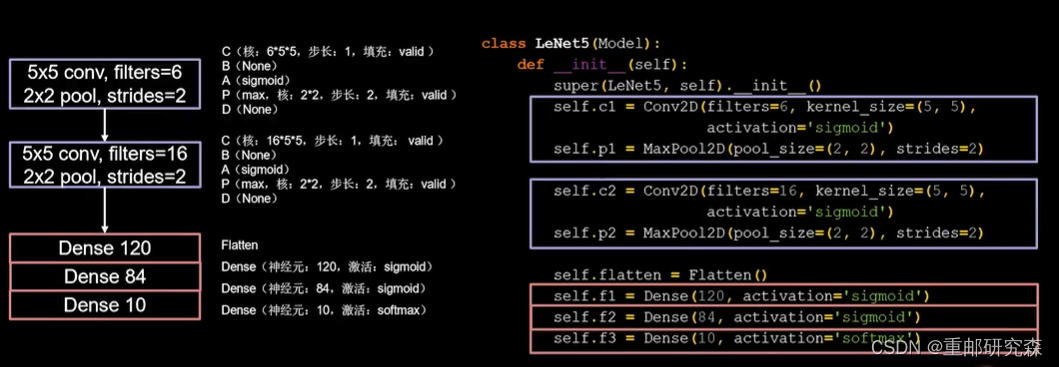
LeNet网络结构

五层网络结构，使用 sigmod激活，无 BN和舍弃。引用两个卷积层，两个池化层，3个全连接层

特点：开篇之作

lass Baseline(Model):
    def __init__(self):
        super(Baseline, self).__init__()
        self.c1 = Conv2D(filters=6, kernel_size=(5, 5), padding='same')  # 卷积层
        self.b1 = BatchNormalization()  # BN层
        self.a1 = Activation('relu')  # 激活层
        self.p1 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')  # 池化层
        self.d1 = Dropout(0.2)  # dropout层

        self.flatten = Flatten()
        self.f1 = Dense(128, activation='relu')
        self.d2 = Dropout(0.2)
        self.f2 = Dense(10, activation='softmax')

    def call(self, x):
        x = self.c1(x)
        x = self.b1(x)
        x = self.a1(x)
        x = self.p1(x)
        x = self.d1(x)

        x = self.flatten(x)
        x = self.f1(x)
        x = self.d2(x)
        y = self.f2(x)
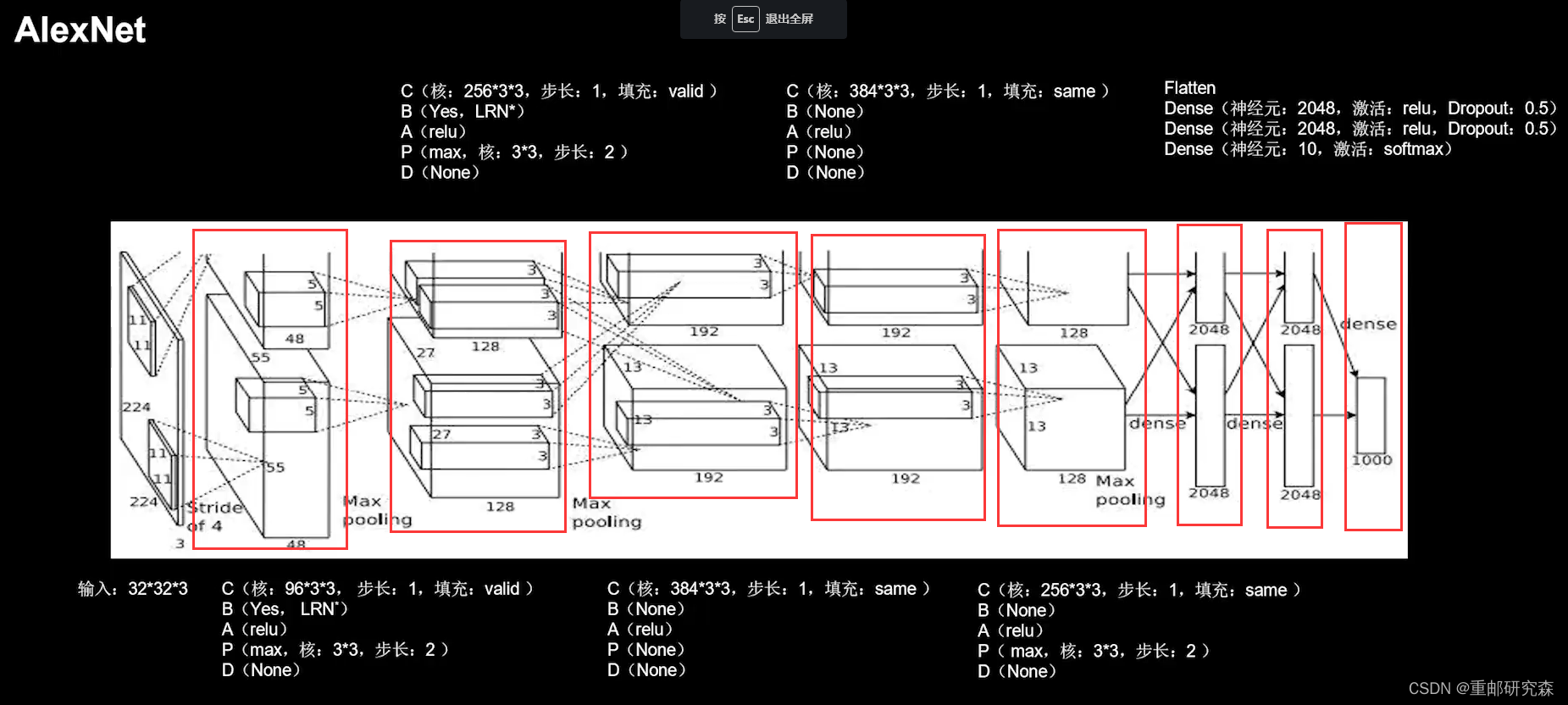
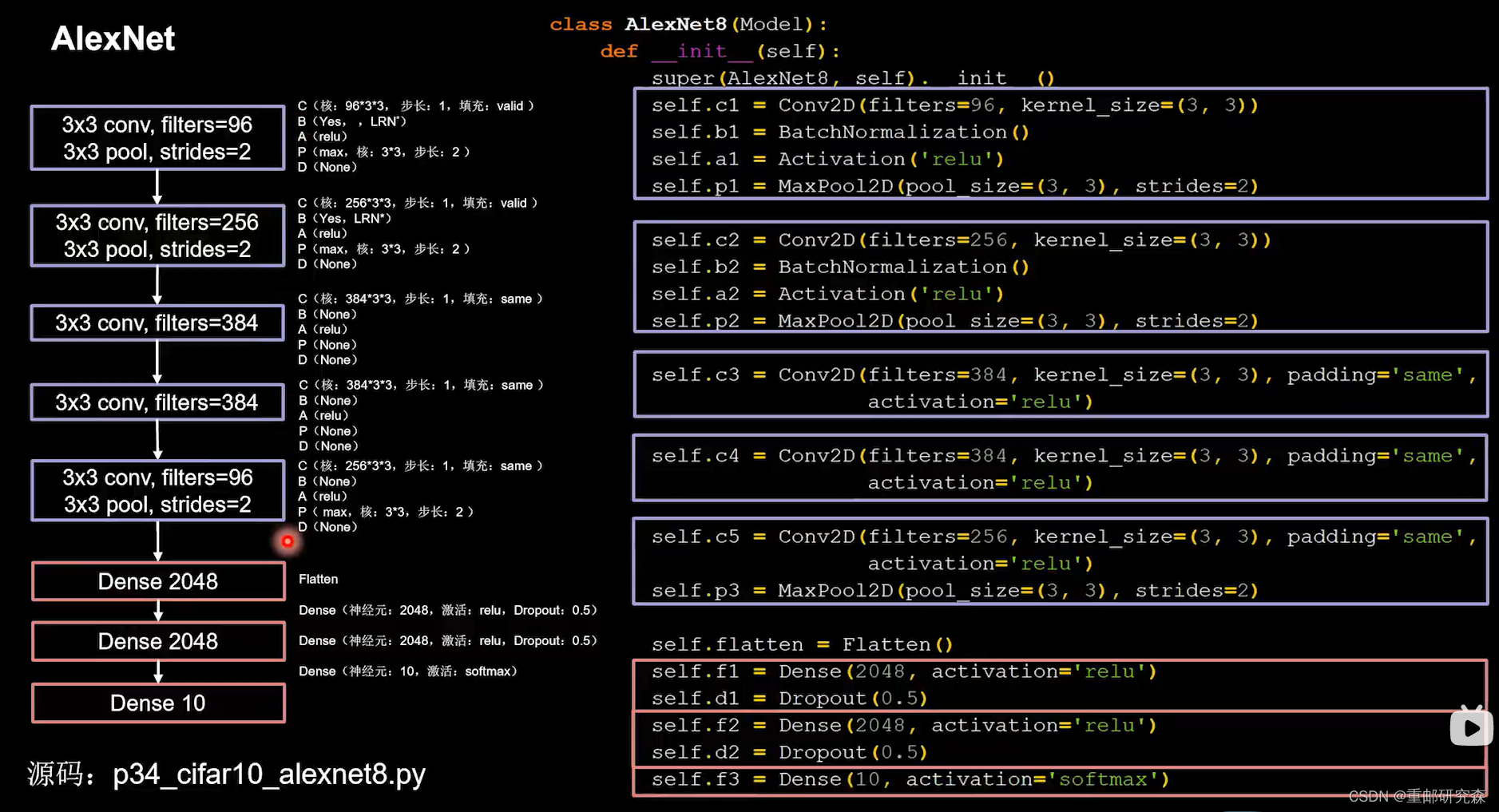
        return y

AlexNet网络结构

8层网络，引入了 relu 激活函数，有BN有舍弃。五层卷积层，3层全连接层

特点：使用 relu激活函数提升训练速度，使用舍弃缓解过拟合

class AlexNet8(Model):
    def __init__(self):
        super(AlexNet8, self).__init__()
        self.c1 = Conv2D(filters=96, kernel_size=(3, 3))
        self.b1 = BatchNormalization()
        self.a1 = Activation('relu')
        self.p1 = MaxPool2D(pool_size=(3, 3), strides=2)

        self.c2 = Conv2D(filters=256, kernel_size=(3, 3))
        self.b2 = BatchNormalization()
        self.a2 = Activation('relu')
        self.p2 = MaxPool2D(pool_size=(3, 3), strides=2)

        self.c3 = Conv2D(filters=384, kernel_size=(3, 3), padding='same',
                         activation='relu')
                         
        self.c4 = Conv2D(filters=384, kernel_size=(3, 3), padding='same',
                         activation='relu')
                         
        self.c5 = Conv2D(filters=256, kernel_size=(3, 3), padding='same',
                         activation='relu')
        self.p3 = MaxPool2D(pool_size=(3, 3), strides=2)

        self.flatten = Flatten()
        self.f1 = Dense(2048, activation='relu')
        self.d1 = Dropout(0.5)
        self.f2 = Dense(2048, activation='relu')
        self.d2 = Dropout(0.5)
        self.f3 = Dense(10, activation='softmax')

    def call(self, x):
        x = self.c1(x)
        x = self.b1(x)
        x = self.a1(x)
        x = self.p1(x)

        x = self.c2(x)
        x = self.b2(x)
        x = self.a2(x)
        x = self.p2(x)

        x = self.c3(x)

        x = self.c4(x)

        x = self.c5(x)
        x = self.p3(x)

        x = self.flatten(x)
        x = self.f1(x)
        x = self.d1(x)
        x = self.f2(x)
        x = self.d2(x)
        y = self.f3(x)
        return y

VGGNet网络结构

16层网络结构，按照CBA->CBAPD重复16个结构，加3层全连接层，通过增加卷积核个数，增加图像深度

特点：小尺寸卷积核，适合并行加速

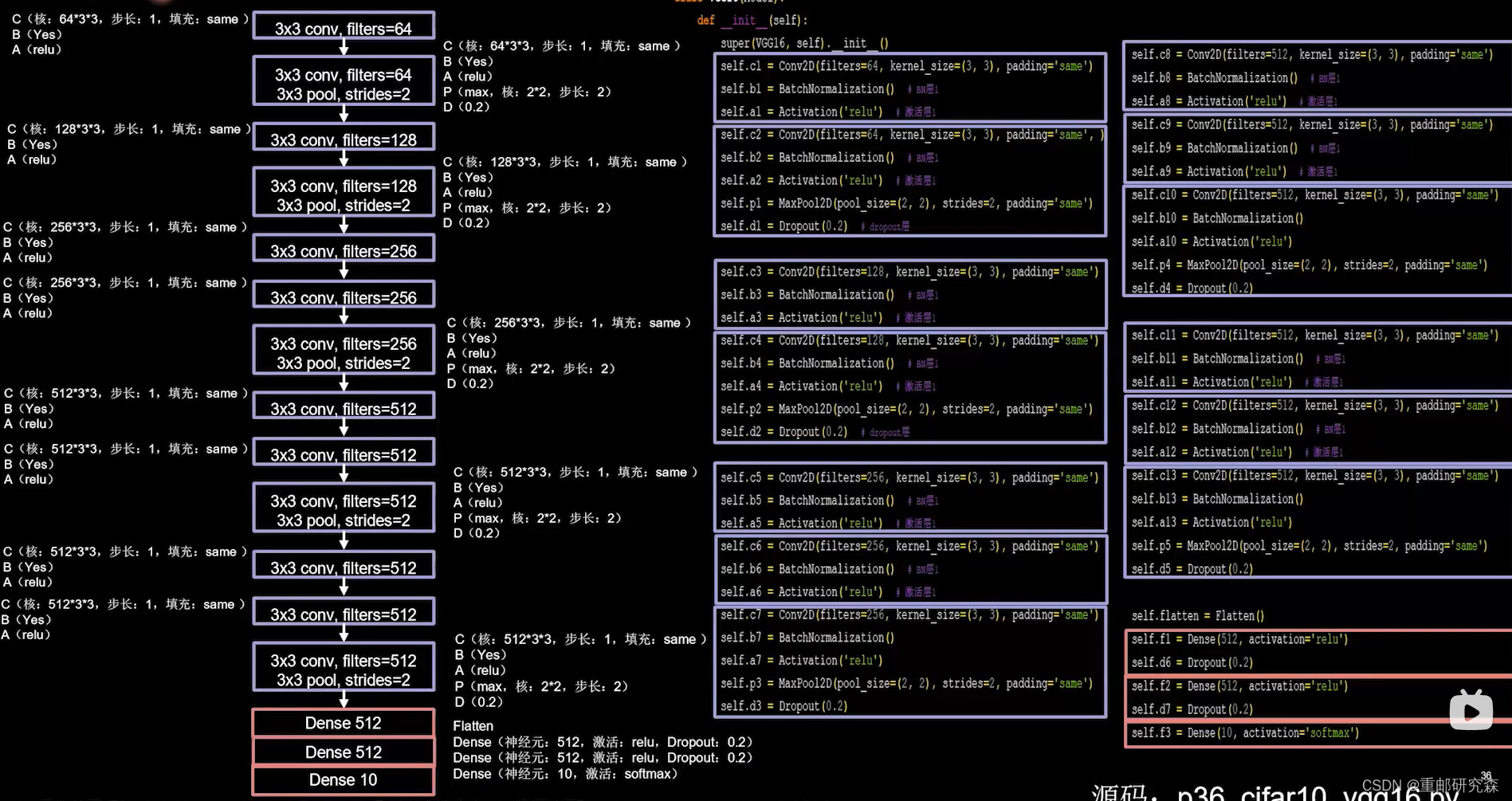
class VGG16(Model):
    def __init__(self):
        super(VGG16, self).__init__()
        self.c1 = Conv2D(filters=64, kernel_size=(3, 3), padding='same')  # 卷积层1
        self.b1 = BatchNormalization()  # BN层1
        self.a1 = Activation('relu')  # 激活层1
        self.c2 = Conv2D(filters=64, kernel_size=(3, 3), padding='same', )
        self.b2 = BatchNormalization()  # BN层1
        self.a2 = Activation('relu')  # 激活层1
        self.p1 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d1 = Dropout(0.2)  # dropout层

        self.c3 = Conv2D(filters=128, kernel_size=(3, 3), padding='same')
        self.b3 = BatchNormalization()  # BN层1
        self.a3 = Activation('relu')  # 激活层1
        self.c4 = Conv2D(filters=128, kernel_size=(3, 3), padding='same')
        self.b4 = BatchNormalization()  # BN层1
        self.a4 = Activation('relu')  # 激活层1
        self.p2 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d2 = Dropout(0.2)  # dropout层

        self.c5 = Conv2D(filters=256, kernel_size=(3, 3), padding='same')
        self.b5 = BatchNormalization()  # BN层1
        self.a5 = Activation('relu')  # 激活层1
        self.c6 = Conv2D(filters=256, kernel_size=(3, 3), padding='same')
        self.b6 = BatchNormalization()  # BN层1
        self.a6 = Activation('relu')  # 激活层1
        self.c7 = Conv2D(filters=256, kernel_size=(3, 3), padding='same')
        self.b7 = BatchNormalization()
        self.a7 = Activation('relu')
        self.p3 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d3 = Dropout(0.2)

        self.c8 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b8 = BatchNormalization()  # BN层1
        self.a8 = Activation('relu')  # 激活层1
        self.c9 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b9 = BatchNormalization()  # BN层1
        self.a9 = Activation('relu')  # 激活层1
        self.c10 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b10 = BatchNormalization()
        self.a10 = Activation('relu')
        self.p4 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d4 = Dropout(0.2)

        self.c11 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b11 = BatchNormalization()  # BN层1
        self.a11 = Activation('relu')  # 激活层1
        self.c12 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b12 = BatchNormalization()  # BN层1
        self.a12 = Activation('relu')  # 激活层1
        self.c13 = Conv2D(filters=512, kernel_size=(3, 3), padding='same')
        self.b13 = BatchNormalization()
        self.a13 = Activation('relu')
        self.p5 = MaxPool2D(pool_size=(2, 2), strides=2, padding='same')
        self.d5 = Dropout(0.2)

        self.flatten = Flatten()
        self.f1 = Dense(512, activation='relu')
        self.d6 = Dropout(0.2)
        self.f2 = Dense(512, activation='relu')
        self.d7 = Dropout(0.2)
        self.f3 = Dense(10, activation='softmax')

    def call(self, x):
        x = self.c1(x)
        x = self.b1(x)
        x = self.a1(x)
        x = self.c2(x)
        x = self.b2(x)
        x = self.a2(x)
        x = self.p1(x)
        x = self.d1(x)

        x = self.c3(x)
        x = self.b3(x)
        x = self.a3(x)
        x = self.c4(x)
        x = self.b4(x)
        x = self.a4(x)
        x = self.p2(x)
        x = self.d2(x)

        x = self.c5(x)
        x = self.b5(x)
        x = self.a5(x)
        x = self.c6(x)
        x = self.b6(x)
        x = self.a6(x)
        x = self.c7(x)
        x = self.b7(x)
        x = self.a7(x)
        x = self.p3(x)
        x = self.d3(x)

        x = self.c8(x)
        x = self.b8(x)
        x = self.a8(x)
        x = self.c9(x)
        x = self.b9(x)
        x = self.a9(x)
        x = self.c10(x)
        x = self.b10(x)
        x = self.a10(x)
        x = self.p4(x)
        x = self.d4(x)

        x = self.c11(x)
        x = self.b11(x)
        x = self.a11(x)
        x = self.c12(x)
        x = self.b12(x)
        x = self.a12(x)
        x = self.c13(x)
        x = self.b13(x)
        x = self.a13(x)
        x = self.p5(x)
        x = self.d5(x)

        x = self.flatten(x)
        x = self.f1(x)
        x = self.d6(x)
        x = self.f2(x)
        x = self.d7(x)
        y = self.f3(x)
        return y

IncepetionNet网络结构

一层网络结构中引入多个尺寸不同卷积核，引入了整改的BN

特点：一层多个不同尺寸卷积核，提升感知力，使用BN缓解梯度消失

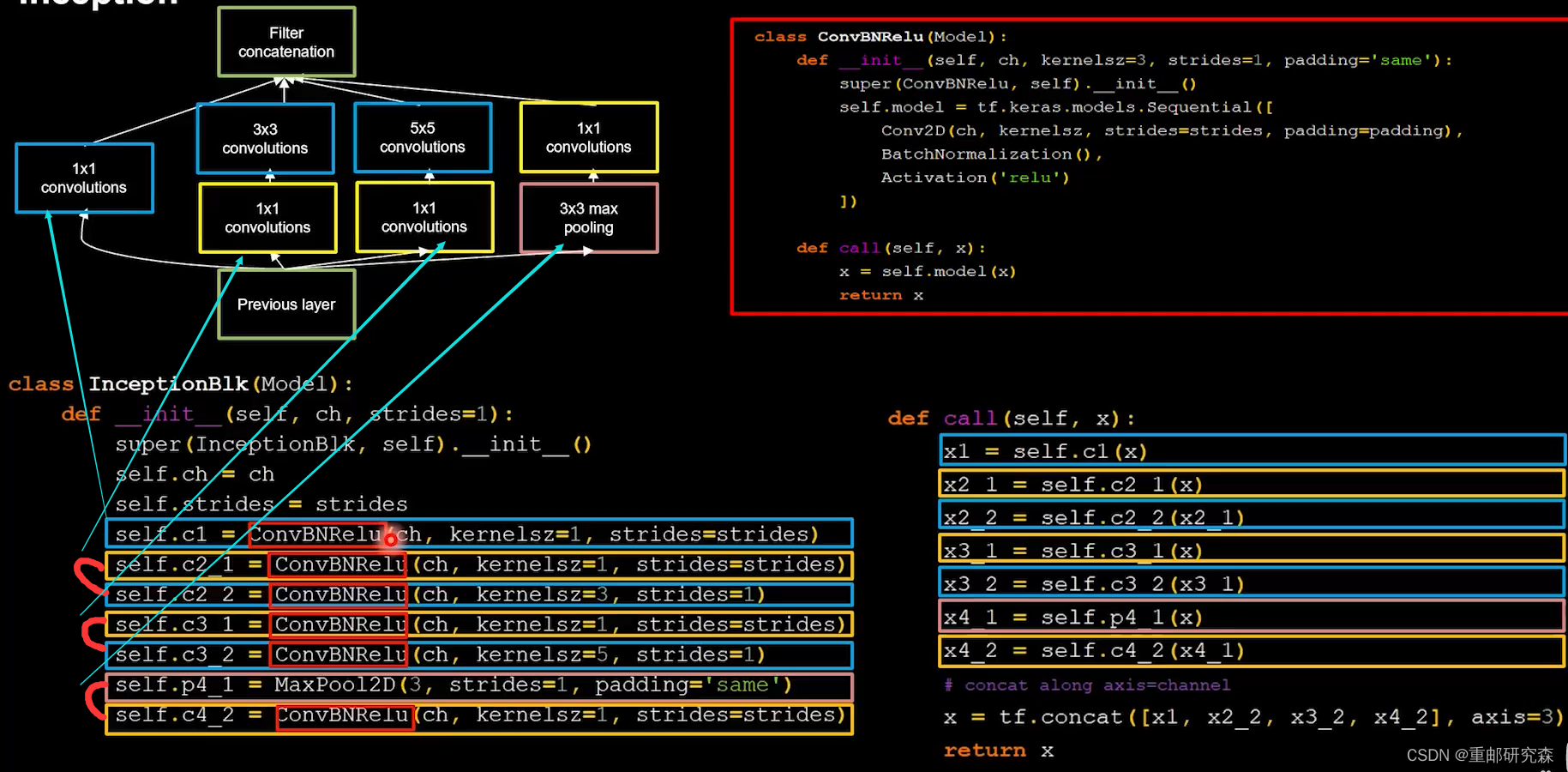
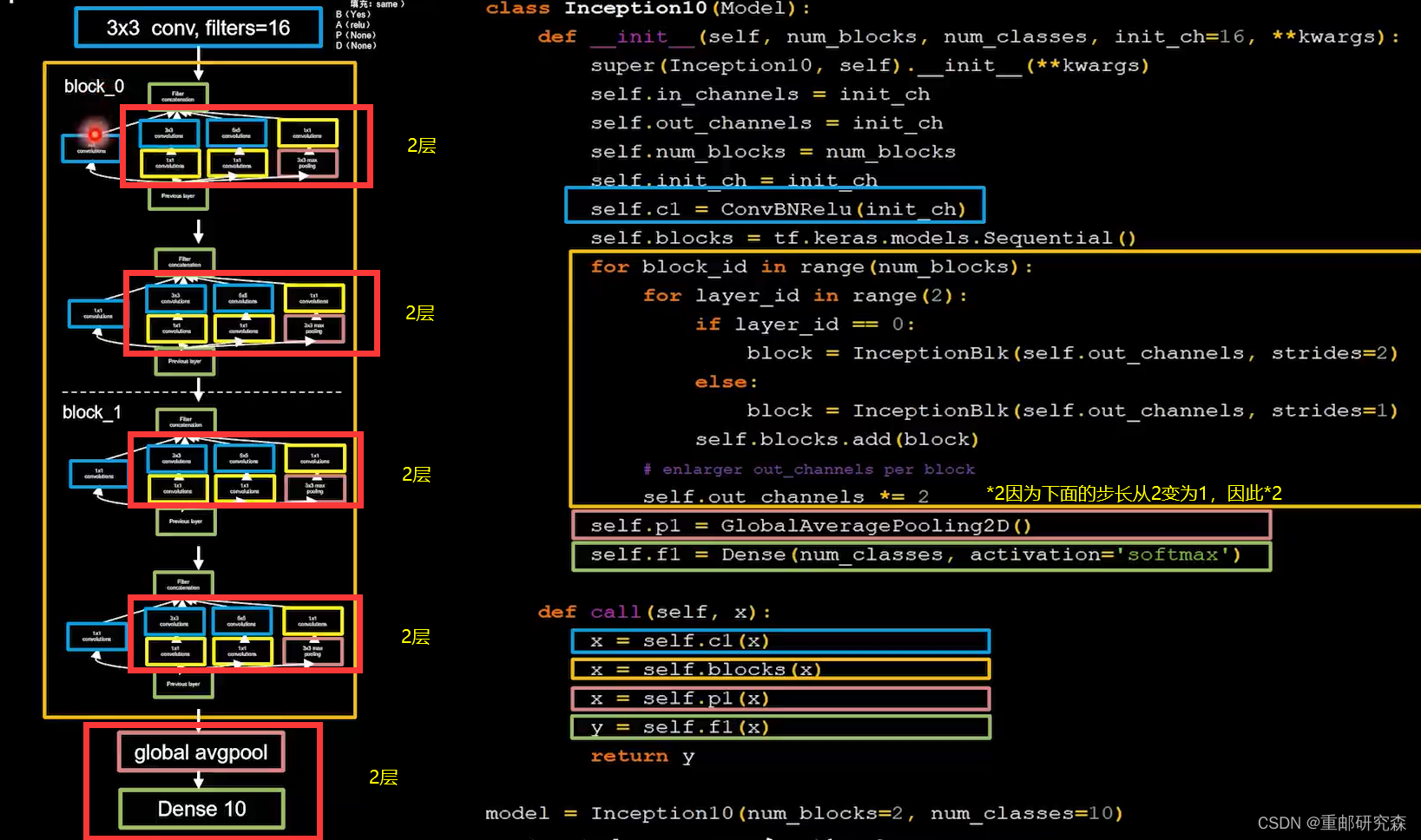
class ConvBNRelu(Model):
    def __init__(self, ch, kernelsz=3, strides=1, padding='same'):
        super(ConvBNRelu, self).__init__()
        self.model = tf.keras.models.Sequential([
            Conv2D(ch, kernelsz, strides=strides, padding=padding),
            BatchNormalization(),
            Activation('relu')
        ])

    def call(self, x):
        x = self.model(x, training=False) #在training=False时，BN通过整个训练集计算均值、方差去做批归一化，training=True时，通过当前batch的均值、方差去做批归一化。推理时 training=False效果好
        return x


class InceptionBlk(Model):
    def __init__(self, ch, strides=1):
        super(InceptionBlk, self).__init__()
        self.ch = ch
        self.strides = strides
        self.c1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
        self.c2_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
        self.c2_2 = ConvBNRelu(ch, kernelsz=3, strides=1)
        self.c3_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
        self.c3_2 = ConvBNRelu(ch, kernelsz=5, strides=1)
        self.p4_1 = MaxPool2D(3, strides=1, padding='same')
        self.c4_2 = ConvBNRelu(ch, kernelsz=1, strides=strides)

    def call(self, x):
        x1 = self.c1(x)
        x2_1 = self.c2_1(x)
        x2_2 = self.c2_2(x2_1)
        x3_1 = self.c3_1(x)
        x3_2 = self.c3_2(x3_1)
        x4_1 = self.p4_1(x)
        x4_2 = self.c4_2(x4_1)
        # concat along axis=channel
        x = tf.concat([x1, x2_2, x3_2, x4_2], axis=3)
        return x

ResNet网络结构

提出了层间残差跳连，使网络结构不断增加提供了保障。具体方法是把网络结构最后输出的特征直接加上原始数据特征

直接相加分为两种情况，也就是F和x维度相同和不同的情况

特点：层间残差链接，缓解模型退化，加深网络层数

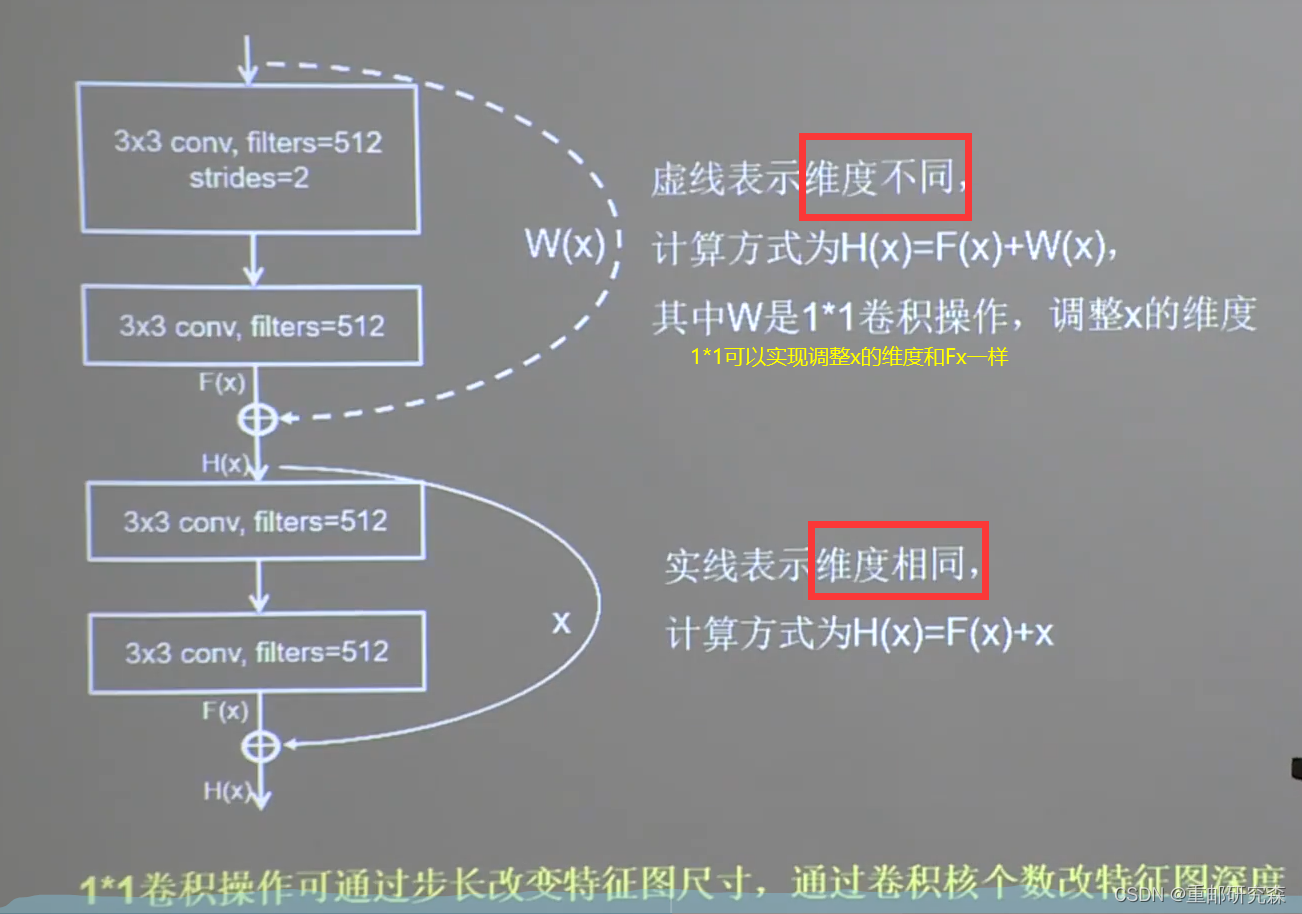
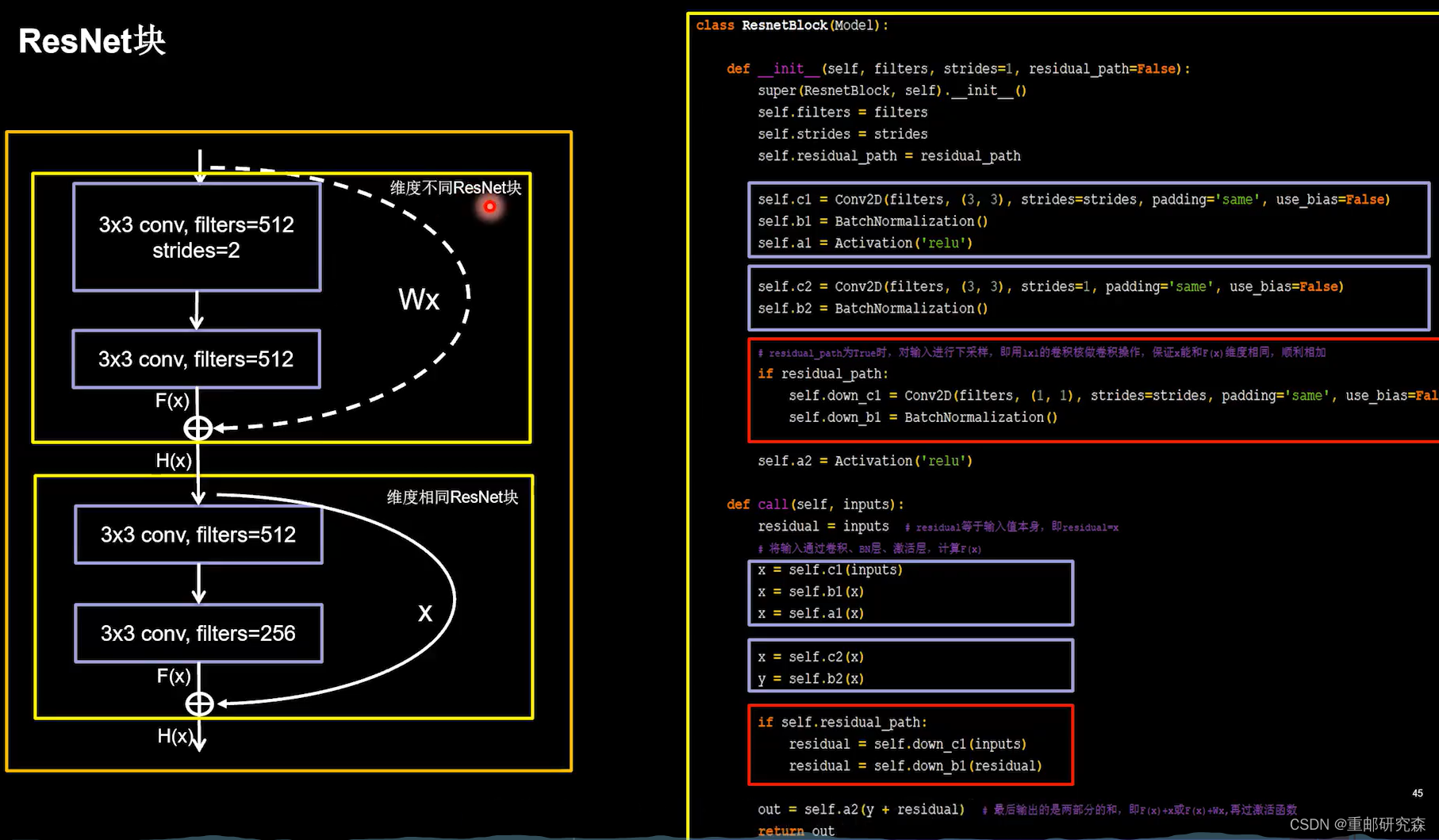
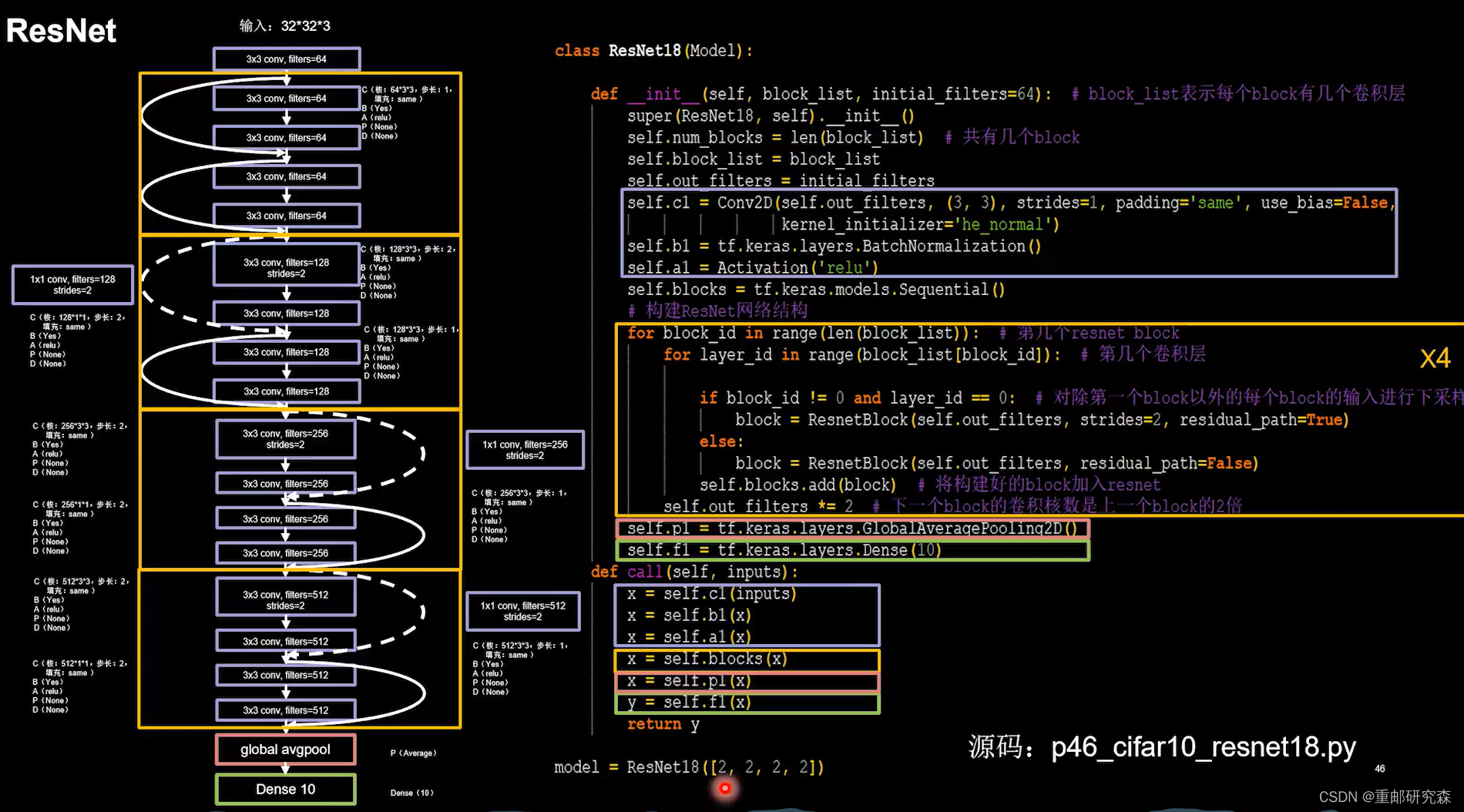
class ResnetBlock(Model):

    def __init__(self, filters, strides=1, residual_path=False):
        super(ResnetBlock, self).__init__()
        self.filters = filters
        self.strides = strides
        self.residual_path = residual_path

        self.c1 = Conv2D(filters, (3, 3), strides=strides, padding='same', use_bias=False)
        self.b1 = BatchNormalization()
        self.a1 = Activation('relu')

        self.c2 = Conv2D(filters, (3, 3), strides=1, padding='same', use_bias=False)
        self.b2 = BatchNormalization()

        # residual_path为True时，对输入进行下采样，即用1x1的卷积核做卷积操作，保证x能和F(x)维度相同，顺利相加
        if residual_path:
            self.down_c1 = Conv2D(filters, (1, 1), strides=strides, padding='same', use_bias=False)
            self.down_b1 = BatchNormalization()
        
        self.a2 = Activation('relu')

    def call(self, inputs):
        residual = inputs  # residual等于输入值本身，即residual=x
        # 将输入通过卷积、BN层、激活层，计算F(x)
        x = self.c1(inputs)
        x = self.b1(x)
        x = self.a1(x)

        x = self.c2(x)
        y = self.b2(x)

        if self.residual_path:
            residual = self.down_c1(inputs)
            residual = self.down_b1(residual)

        out = self.a2(y + residual)  # 最后输出的是两部分的和，即F(x)+x或F(x)+Wx,再过激活函数
        return out


class ResNet18(Model):

    def __init__(self, block_list, initial_filters=64):  # block_list表示每个block有几个卷积层
        super(ResNet18, self).__init__()
        self.num_blocks = len(block_list)  # 共有几个block
        self.block_list = block_list
        self.out_filters = initial_filters
        self.c1 = Conv2D(self.out_filters, (3, 3), strides=1, padding='same', use_bias=False)
        self.b1 = BatchNormalization()
        self.a1 = Activation('relu')
        self.blocks = tf.keras.models.Sequential()
        # 构建ResNet网络结构
        for block_id in range(len(block_list)):  # 第几个resnet block
            for layer_id in range(block_list[block_id]):  # 第几个卷积层

                if block_id != 0 and layer_id == 0:  # 对除第一个block以外的每个block的输入进行下采样
                    block = ResnetBlock(self.out_filters, strides=2, residual_path=True)
                else:
                    block = ResnetBlock(self.out_filters, residual_path=False)
                self.blocks.add(block)  # 将构建好的block加入resnet
            self.out_filters *= 2  # 下一个block的卷积核数是上一个block的2倍
        self.p1 = tf.keras.layers.GlobalAveragePooling2D()
        self.f1 = tf.keras.layers.Dense(10, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())

    def call(self, inputs):
        x = self.c1(inputs)
        x = self.b1(x)
        x = self.a1(x)
        x = self.blocks(x)
        x = self.p1(x)
        y = self.f1(x)
        return y

循环神经网络

针对时间序列数据，利用RNN循环神经网络进行预测。这里利用的原理是：下一个时刻的输出和历史数据的关系

循环核

定义：循环核具有记忆力，通过对参数时间的共享，实现了对时间序列的信息提取

循环核按时间步展开

把循环核按时间序列展开，相当于循环核不断更新，而我们预测时采取的是更新到最好的那个参数矩阵。就类似人背书，会训练到人滚瓜烂熟的时候，进行预测

循环计算层

x个循环核构成x个循环计算层

TF描述循环计算层

TF对输入数据有要求，必须三维，具体要求如下：

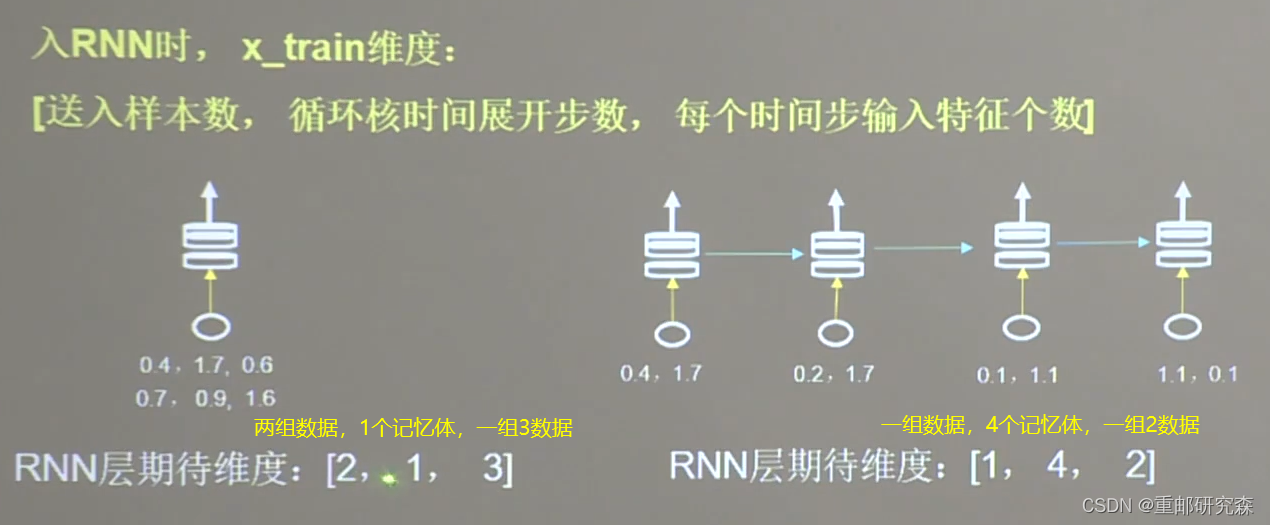
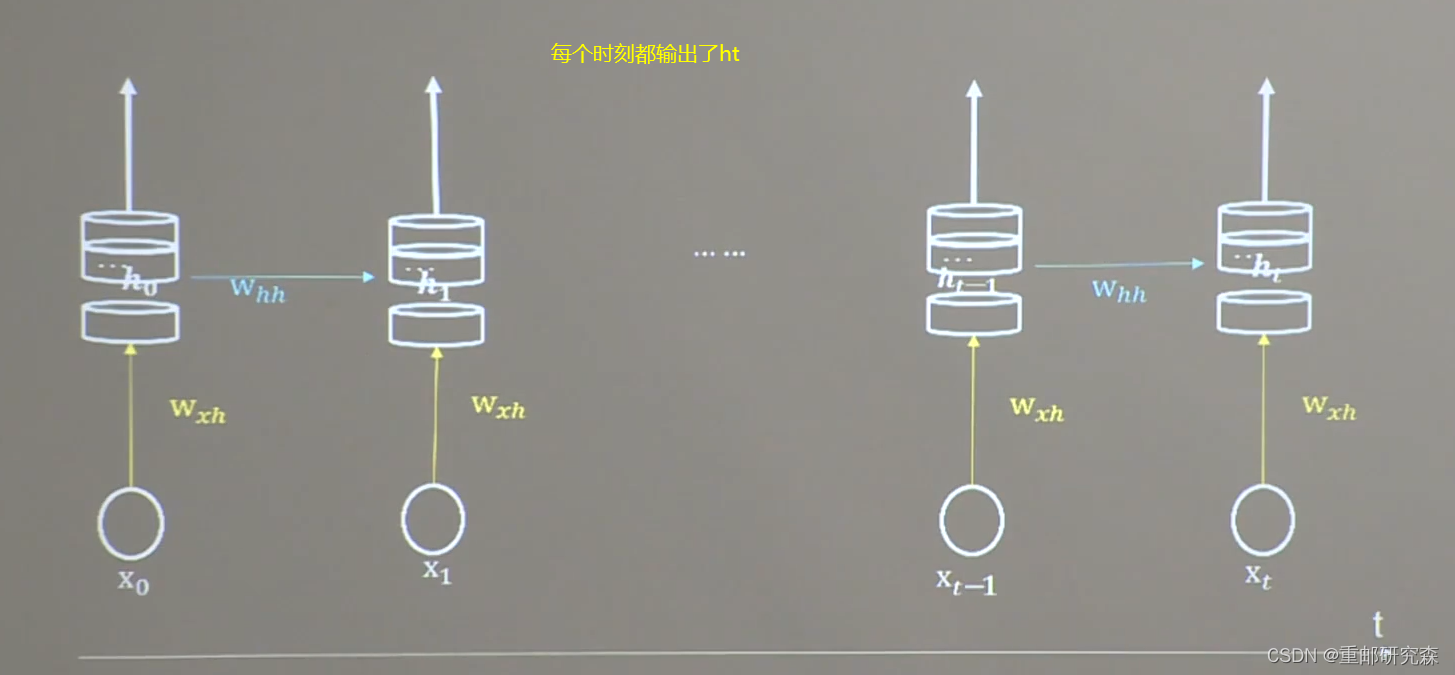
字母预测独热码

单字母预测

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN
import matplotlib.pyplot as plt
import os

input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4}  # 单词映射到数值id的词典
id_to_onehot = {0: [1., 0., 0., 0., 0.], 1: [0., 1., 0., 0., 0.], 2: [0., 0., 1., 0., 0.], 3: [0., 0., 0., 1., 0.],
                4: [0., 0., 0., 0., 1.]}  # id编码为one-hot

x_train = [id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']],
           id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']]]
y_train = [w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e'], w_to_id['a']]

np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)

# 使x_train符合SimpleRNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]。
# 此处整个数据集送入，送入样本数为len(x_train)；输入1个字母出结果，循环核时间展开步数为1; 表示为独热码有5个输入特征，每个时间步输入特征个数为5
x_train = np.reshape(x_train, (len(x_train), 1, 5))
y_train = np.array(y_train)

model = tf.keras.Sequential([
    SimpleRNN(3),
    Dense(5, activation='softmax')
])

model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

checkpoint_save_path = "./checkpoint/rnn_onehot_1pre1.ckpt"

if os.path.exists(checkpoint_save_path + '.index'):
    print('-------------load the model-----------------')
    model.load_weights(checkpoint_save_path)

cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
                                                 save_weights_only=True,
                                                 save_best_only=True,
                                                 monitor='loss')  # 由于fit没有给出测试集，不计算测试集准确率，根据loss，保存最优模型

history = model.fit(x_train, y_train, batch_size=32, epochs=100, callbacks=[cp_callback])

model.summary()

# print(model.trainable_variables)
file = open('./weights.txt', 'w')  # 参数提取
for v in model.trainable_variables:
    file.write(str(v.name) + '\n')
    file.write(str(v.shape) + '\n')
    file.write(str(v.numpy()) + '\n')
file.close()

###############################################    show   ###############################################

# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
loss = history.history['loss']

plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.title('Training Accuracy')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()

############### predict #############

preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
    alphabet1 = input("input test alphabet:")
    alphabet = [id_to_onehot[w_to_id[alphabet1]]]
    # 使alphabet符合SimpleRNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]。此处验证效果送入了1个样本，送入样本数为1；输入1个字母出结果，所以循环核时间展开步数为1; 表示为独热码有5个输入特征，每个时间步输入特征个数为5
    alphabet = np.reshape(alphabet, (1, 1, 5))
    result = model.predict(alphabet)
    pred = tf.argmax(result, axis=1)
    pred = int(pred)
    tf.print(alphabet1 + '->' + input_word[pred])

多字母预测

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN
import matplotlib.pyplot as plt
import os

input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4}  # 单词映射到数值id的词典
id_to_onehot = {0: [1., 0., 0., 0., 0.], 1: [0., 1., 0., 0., 0.], 2: [0., 0., 1., 0., 0.], 3: [0., 0., 0., 1., 0.],
                4: [0., 0., 0., 0., 1.]}  # id编码为one-hot

x_train = [
    [id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']]],
    [id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']]],
    [id_to_onehot[w_to_id['c']], id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']]],
    [id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']]],
    [id_to_onehot[w_to_id['e']], id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']]],
]
y_train = [w_to_id['e'], w_to_id['a'], w_to_id['b'], w_to_id['c'], w_to_id['d']]

np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)

# 使x_train符合SimpleRNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]。
# 此处整个数据集送入，送入样本数为len(x_train)；输入4个字母出结果，循环核时间展开步数为4; 表示为独热码有5个输入特征，每个时间步输入特征个数为5
x_train = np.reshape(x_train, (len(x_train), 4, 5))
y_train = np.array(y_train)

model = tf.keras.Sequential([
    SimpleRNN(3),
    Dense(5, activation='softmax')
])

model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

checkpoint_save_path = "./checkpoint/rnn_onehot_4pre1.ckpt"

if os.path.exists(checkpoint_save_path + '.index'):
    print('-------------load the model-----------------')
    model.load_weights(checkpoint_save_path)

cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
                                                 save_weights_only=True,
                                                 save_best_only=True,
                                                 monitor='loss')  # 由于fit没有给出测试集，不计算测试集准确率，根据loss，保存最优模型

history = model.fit(x_train, y_train, batch_size=32, epochs=100, callbacks=[cp_callback])

model.summary()

# print(model.trainable_variables)
file = open('./weights.txt', 'w')  # 参数提取
for v in model.trainable_variables:
    file.write(str(v.name) + '\n')
    file.write(str(v.shape) + '\n')
    file.write(str(v.numpy()) + '\n')
file.close()

###############################################    show   ###############################################

# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
loss = history.history['loss']

plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.title('Training Accuracy')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()

############### predict #############

preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
    alphabet1 = input("input test alphabet:")
    alphabet = [id_to_onehot[w_to_id[a]] for a in alphabet1]
    # 使alphabet符合SimpleRNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]。此处验证效果送入了1个样本，送入样本数为1；输入4个字母出结果，所以循环核时间展开步数为4; 表示为独热码有5个输入特征，每个时间步输入特征个数为5
    alphabet = np.reshape(alphabet, (1, 4, 5))
    result = model.predict(alphabet)
    pred = tf.argmax(result, axis=1)
    pred = int(pred)
    tf.print(alphabet1 + '->' + input_word[pred])

字母预测Embedding码

定义：Embedding可以降低维度，因为独热码数据过大，数据有几个码元就需要几个

输入数据要求：

单字母预测

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN, Embedding
import matplotlib.pyplot as plt
import os

input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4}  # 单词映射到数值id的词典

x_train = [w_to_id['a'], w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e']]
y_train = [w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e'], w_to_id['a']]

np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)

# 使x_train符合Embedding输入要求：[送入样本数， 循环核时间展开步数] ，
# 此处整个数据集送入所以送入，送入样本数为len(x_train)；输入1个字母出结果，循环核时间展开步数为1。
x_train = np.reshape(x_train, (len(x_train), 1))
y_train = np.array(y_train)

model = tf.keras.Sequential([
    Embedding(5, 2),
    SimpleRNN(3),
    Dense(5, activation='softmax')
])

model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

checkpoint_save_path = "./checkpoint/run_embedding_1pre1.ckpt"

if os.path.exists(checkpoint_save_path + '.index'):
    print('-------------load the model-----------------')
    model.load_weights(checkpoint_save_path)

cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
                                                 save_weights_only=True,
                                                 save_best_only=True,
                                                 monitor='loss')  # 由于fit没有给出测试集，不计算测试集准确率，根据loss，保存最优模型

history = model.fit(x_train, y_train, batch_size=32, epochs=100, callbacks=[cp_callback])

model.summary()

# print(model.trainable_variables)
file = open('./weights.txt', 'w')  # 参数提取
for v in model.trainable_variables:
    file.write(str(v.name) + '\n')
    file.write(str(v.shape) + '\n')
    file.write(str(v.numpy()) + '\n')
file.close()

###############################################    show   ###############################################

# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
loss = history.history['loss']

plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.title('Training Accuracy')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()

############### predict #############

preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
    alphabet1 = input("input test alphabet:")
    alphabet = [w_to_id[alphabet1]]
    # 使alphabet符合Embedding输入要求：[送入样本数， 循环核时间展开步数]。
    # 此处验证效果送入了1个样本，送入样本数为1；输入1个字母出结果，循环核时间展开步数为1。
    alphabet = np.reshape(alphabet, (1, 1))
    result = model.predict(alphabet)
    pred = tf.argmax(result, axis=1)
    pred = int(pred)
    tf.print(alphabet1 + '->' + input_word[pred])

多字母预测

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN, Embedding
import matplotlib.pyplot as plt
import os

input_word = "abcdefghijklmnopqrstuvwxyz"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4,
           'f': 5, 'g': 6, 'h': 7, 'i': 8, 'j': 9,
           'k': 10, 'l': 11, 'm': 12, 'n': 13, 'o': 14,
           'p': 15, 'q': 16, 'r': 17, 's': 18, 't': 19,
           'u': 20, 'v': 21, 'w': 22, 'x': 23, 'y': 24, 'z': 25}  # 单词映射到数值id的词典

training_set_scaled = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
                       11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
                       21, 22, 23, 24, 25]

x_train = []
y_train = []

for i in range(4, 26):
    x_train.append(training_set_scaled[i - 4:i])
    y_train.append(training_set_scaled[i])

np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)

# 使x_train符合Embedding输入要求：[送入样本数， 循环核时间展开步数] ，
# 此处整个数据集送入所以送入，送入样本数为len(x_train)；输入4个字母出结果，循环核时间展开步数为4。
x_train = np.reshape(x_train, (len(x_train), 4))
y_train = np.array(y_train)

model = tf.keras.Sequential([
    Embedding(26, 2),
    SimpleRNN(10),
    Dense(26, activation='softmax')
])

model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

checkpoint_save_path = "./checkpoint/rnn_embedding_4pre1.ckpt"

if os.path.exists(checkpoint_save_path + '.index'):
    print('-------------load the model-----------------')
    model.load_weights(checkpoint_save_path)

cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
                                                 save_weights_only=True,
                                                 save_best_only=True,
                                                 monitor='loss')  # 由于fit没有给出测试集，不计算测试集准确率，根据loss，保存最优模型

history = model.fit(x_train, y_train, batch_size=32, epochs=100, callbacks=[cp_callback])

model.summary()

file = open('./weights.txt', 'w')  # 参数提取
for v in model.trainable_variables:
    file.write(str(v.name) + '\n')
    file.write(str(v.shape) + '\n')
    file.write(str(v.numpy()) + '\n')
file.close()

###############################################    show   ###############################################

# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
loss = history.history['loss']

plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.title('Training Accuracy')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()

################# predict ##################

preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
    alphabet1 = input("input test alphabet:")
    alphabet = [w_to_id[a] for a in alphabet1]
    # 使alphabet符合Embedding输入要求：[送入样本数， 时间展开步数]。
    # 此处验证效果送入了1个样本，送入样本数为1；输入4个字母出结果，循环核时间展开步数为4。
    alphabet = np.reshape(alphabet, (1, 4))
    result = model.predict([alphabet])
    pred = tf.argmax(result, axis=1)
    pred = int(pred)
    tf.print(alphabet1 + '->' + input_word[pred])