世界三大数学猜想的证明(李扩继)

世界三大数学猜想，即哥德巴赫猜想，四色猜想，费马猜想。哥猜和费马猜想都是数论问题，四色猜想是图论问题也归结为数论问题。它们好似一个神秘地深不可测的原始森林，众多者望而生畏，而好奇的探险者入林就迷失方向，虽然它们都经历了数个世纪而不得解，但无论如何它们都应该遵循一个最基本的规律，难在人们无法论证这个规律。我发表的《世界三大数学猜想的论证综述》一文[1]已经二年了，当然，一个数学猜想的证明有必要经过时间的沉淀。我再次叙述一下这三个猜想的证明思想方法。

一，哥猜的证明

素数的存在性，孪生素数的存在性，和哥猜的存在性是统一的问题。处理它们用的都是同一种方法，那就是找到它们的存在数域，再筛去合数。传统的筛法有埃氏筛法，我还发现了欧拉函数筛法，它们都是筛码由小到大筛去合数的，现在倒过来，筛码由大到小筛去合数，我称为这种筛法为颠覆性筛法。这种筛法明确清晰的解决了它们。

 

①素数的存在性问题

命题1，

设A:{1，2，3，…，p^2}，其中p为正整数。那么，数域A中至少有p个素数。

 

证明(颠覆性筛法):用p，p-1，…，3，2作为筛码，由大到小筛除A中能被它们整除的数，留了下来的就是素数，至少留下了p个素数(包括1):，关系式如下:

p^2(1-1/p)(1-1/(p-1))…(1-1/3)(1-1/2)=p。

这个式子的意义请参考文[1]。

直观举例如下:

A:

1.2.3.4.5.6，

7.8.9.10.11.12.

13.14.15.16.17.18.

19.20.21.22.23.24.

25.26.27.28.29.30.

31.32.33.34.35.36.

用6，5，4，3，2作为筛码，由大到小筛除合数与它自身。

6筛除了(6，12，18，24，30，36)共6个合数。

5筛去了(5，10，15，20，25，35)共6个，

4筛除了(4，8，16，28，32)共5个，

3筛除了(3，9，21，27，33)共5个，

2筛除了(2，14，22，26，34)共5个，留下了(1，7，11，13，17，19，23，29，31)共9个素数，1谁都筛不掉留了下来，计算在素数个数中。用6，5，4，3，2作为筛码

素数，关系式表示为

36(1-1/6)(1-1/5)(1-1/4)(1－1/3)(1-1/2)=6。

这里(1-1/6)有明确的意义，就是筛除能被6整除的数后，留下的与6互质的六分之五的数。同样(1-1/5)意义也是如此，而36(1-1/6)(1-1/5)的意义是，36以内正整数中至少与6X5互质的数的个数(=24)。以此类推36(1-1/6)(1-1/5)(1-1/4)(1－1/3)(1-1/2)就表示了与6x5X4x3X2互质的数的个数最小值。

明白了解决了素数的存在性问题的方法，就能证明孪生素数的存在性问题与哥猜问题。

②孪生素数的存在性

命题2:设B:{(1，3)，(2，4)，(3，5)，…，(p^2，p^2+2)}，那么，数域B中，至少存在p/2个(素数，素数)元数的个数。其中，p为正整数。

证明(颠覆性筛法)，若p为奇数，用p，p-2，p-4，…，3，2作为筛码，由大到小筛除能被它们整除的元素(即至少整除元素中的一个数)。因为数域B中，连续的q个元素中，仅有二个元素能被q整除，所以p^2(1-2/p)表示了B中与p互质的元素个数(p与元素中的两个数都互质)，p^2(1-2/p)(1-2/(p-2))表示了B中与px(p-2)互质的元素个数的最小值，以此类推，p^2(1-2/p)(1-2/(p-2))…(l-2/3)(1-1/2)表示了B中与px(p-2)x…x3X2互质的元素个数的最小值，即

p^2(1-2/p)(1-2/(p-2))…(l-2/3)(1-1/2)

=p/2.其中，p为奇数。

 

当p为偶数时，以p，p-1，P-3，…，3，2作为筛码，由大到小筛除能被它们整除的元素，2是偶数，再用偶数p作为筛码是过度的，故仅从B集合中1/p元素个数，于是有关系式

p^2(1-1/p)(1-2/(p-1))…(1-2/3)(1-1/2)

=p/2.其中，p为偶数

所以，B中至少有孪生素数[p/2]个(即元素(素数，素数))。[a]表示正数a的整数部分。

③哥猜的存在性

命题3，设C:{(1，2n-1)，(2，2n-2)，…(p^2，2n-p^2)}，那么，集合C中至少存在[p/4]个(素数，素数)的元素。其中，正整数p满足p^2≤2n。

 

证明(颠覆性筛法):若p为奇数，用p，p-2，p-4，…，3，2作为筛码，由大到小筛除集合C中能被它们整除的元素(即至少整除元素中的一个数)。因为数域C中，连续的q个元素中，若q不整除2n，那么仅有二个元素能被q整除；若q整除2n，那么仅有一个元素能被q整除。所以，当p不整除2n，p^2(1-2/p)表示了C中与p互质的元素个数(p与元素中的两个数都互质)，假设筛码(除2外)都不整除2n，那么，p^2(1-2/p)(1-2/(p-2))表示了C中与px(p-2)互质的元素个数的最小值，以此类推，p^2(1-2/p)(1-2/(p-2))…(l-2/3)(1-1/2)表示了C中与px(p-2)x…x3X2互质的元素个数的最小值，由于C中存在(a，b)与(b，a)对称的元素，故再除以2，即

p^2(1-2/p)(1-2/(p-2))…(l-2/3)(1-1/2)(1/2)

=p/4≥[p/4].其中，p为偶数。

 

所以，C中至少有[p/4]个(素数，素数)的元素。即2n表两个素数之和的个数至少有[p/4]个，其中，p^2≤2n。

二，四色问题猜想的证明

无规则的地图五彩缤纷，有人提出用单色区分国与国或区域与区域，真有数学思维也。

 

四色问题猜想是由英国的弗南西斯·格思里在1852年提出来的. 当时他在一家科研单位从事地图着色工作，发现每幅地图似乎都可以用四种颜色着色，使得有共同边界的国家被着上不同的颜色. 他和弟弟格里斯曾试图证明这一猜想，但未取得进展. 同年10月23日，他的弟弟就该问题请教了其老师德·摩尔根，德·摩尔根也未能找到解决途径，后又写信向哈密顿爵士请教，直至1865年哈密顿逝世，问题仍未解决. 1872年，英国数学家凯利正式向伦敦数学学会提出此问题，四色猜想遂成为世界数学界关注的焦点.

 

四色猜想是由英人提出的，他没有解决，随之成为世界数学猜想。这么大的数学问题，是否有简单的处理方法？有，绝对有至简。

那就是，只研究一个图形与之有公共边的图形即可。要证明它，必须对图形作出数学定义。

 

定义，曲线是由无数个点单连接而成的，面积是由封闭曲线围着的无数个点单连接而成，不是堆积，堆积是体积。封闭曲线是面积的边界。两个面积的公共边至少有两个点。两点构成线段。这里，把多个面积称为图1，图2，…，图n。并且约定图与图之间只有公共边没有重叠。有了这些定义之后，来看下面定理。

 

 

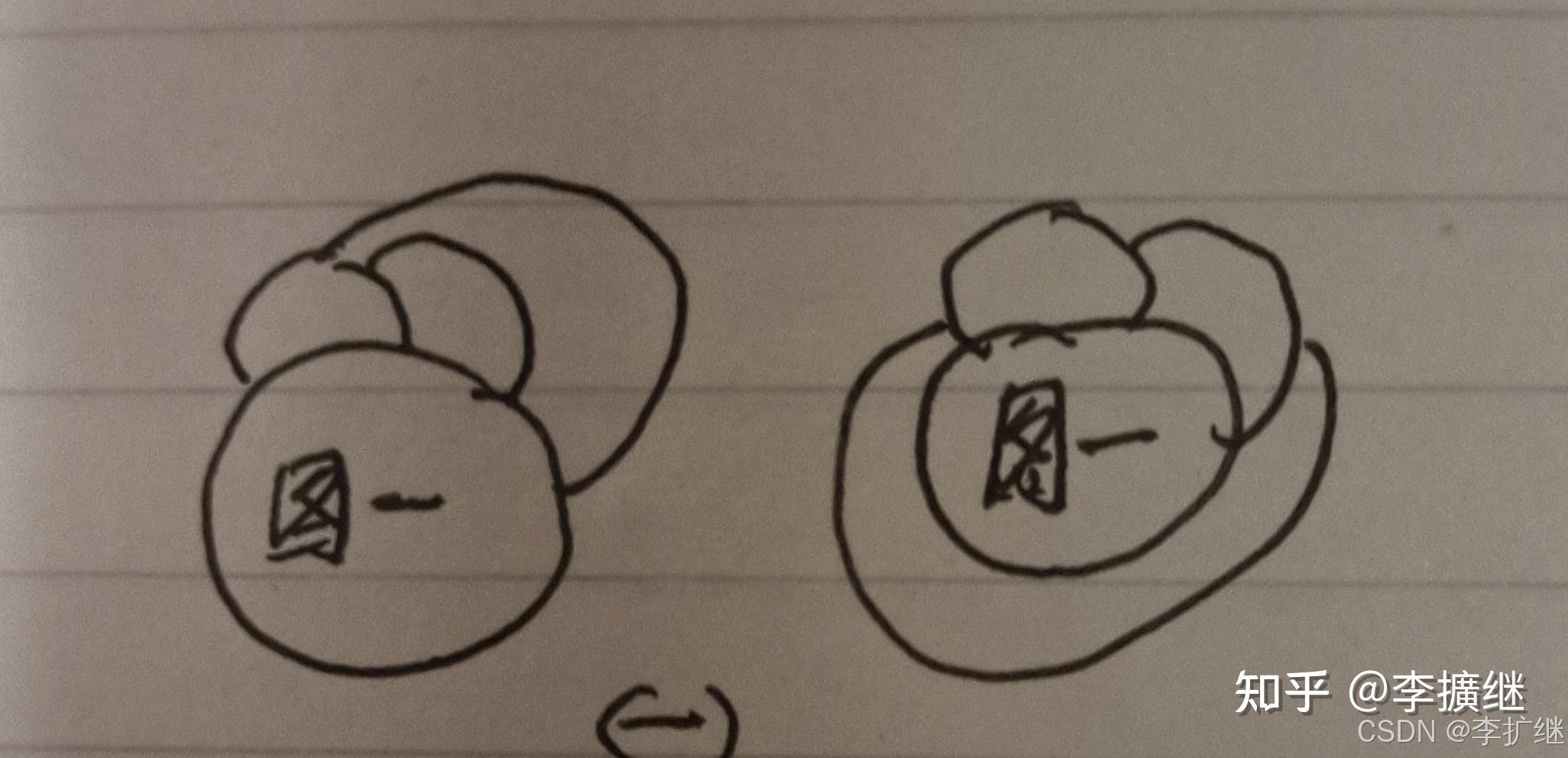
定理1，若n个图形必须要用n种不同的颜色来区分，那么，它们每一个图形与其他n-1个图形都有公共边。

定理2，若四个图形，每一个图形与其他三个图形都有公共边，那么，总有一个图形被其他三个图形全包围。

 

神秘的四色猜想，实际上这两个定理就解决了它，但必须要有一个操作方法，那就是只考查一个图形，谁在依靠它？与它不依靠的图形着什么色和它没有关系。

定理3，巳知n个图形，若n-1个图形与图1都有公共边，那么，这n个图形只要用四种不同的颜色区分就够了。

 

证明:若n-1个图形之间彼此没有公共边，那么区分这个图形只要用二种不同的颜色就够了。所以，考查它们之间有公共边的情况。

它们的排列有两种情形。

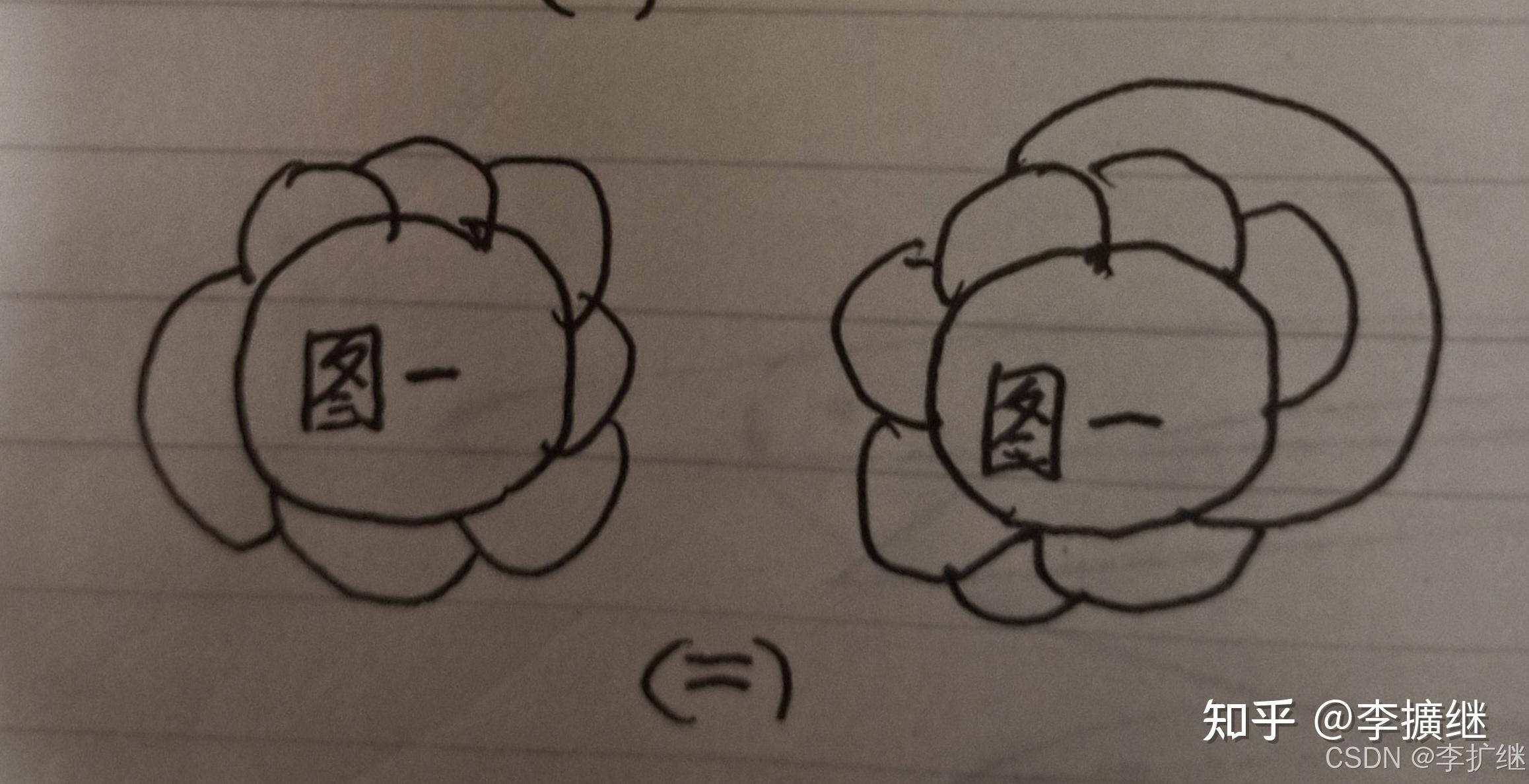
①单一排列，即每一个图形只有三个公共边(包括与图1的一个公共边)。

②复杂排列，即至少有一个图形除与图一有公共边外，与其他图形有二个以上的公共边。如图二所示。

无论单一排列和复杂排列，用四色即可区分它们。

 

定理3告诉我们，给地图着色，可以从任何一个图形开始，给它着色1，再给它有公共边的图形着色，仅四色就足够了，然后再确定一个已经着色的图形，并给与它有公共边的图形着色，四色足够。依此方法，可完成整个地图的着色。

 

综上，四色猜想是怎么样理顺图形的组合排列问题。

三，费马猜想的证明

我国汉代的《周髀算经》中，书中提到商高曾说“勾广三，股修四，径隅五”，意思是当直角三角形的两条直角边分别为3和4时，斜边则为5.，是勾股定理的特例。500年后古希腊数学家毕达哥拉斯（约公元前570 - 约公元前490）及其学派完善了勾股定理一般性。

商高后的1637年左右(夸度大约2500年)，由法国数学家皮埃尔·德·费马提出猜想.其内容为：当整数n>2时，关于x、y、z的方程x^{n}+y^{n}=z^{n}没有正整数解.

费马将“存在两个正整数的平方和等于一个正整数的平方"，推广到“是否存在两个正整数的n(n>2)次方之和等于一个正整数的n次方"的一般问题，费马给出猜想它不存在。费马自己早期证明了n = 4的情形，但他却写了一段话:他“发现了一种美妙的证法，可惜书的空白处太少，写不下"。这句话成为了永久之谜。

推广并没有结束，可以把它推的更广:

命题1，是否存在:三个正整数的n(n≥2)次方之和等于一个正整数的n次方"？

命题2，是否存在:m(m≥2)个正整数的n(n≥2)次方之和等于一个正整数的n次方"？

已经发现反例，下列方程有整数解

①x^3+y^3+z^3=w^3有整数解

 

3^3+4^3+5^3=6^3；

1^3十6^3十8^3=9^3；

(四个未知量三次式的解有无数多)

②四个未知量四次式也有整数解，如

958000^4十217519^4十415560^4=422481^4

 

③x^4+y^4+z^4十a^4=w^4有整数解。如

30^4+120^4+272^4十

 

315^4=353^4；

④x^5+y^5+z^5十a^5=w^5有整数解。如

27^5+84^5+110^5十133^5=144^5；

⑤x^5+y^5+z^5十a^5+b^5=w^5有整数解。如

19^5十43^5十46^5十47^5十67^5=72^5

⑤x^7+y^7+z^7十a^7十b^7十c^7十d^7=w^7有整数解。如

127^7十258^7十266^7十413^7十430^7十439^7十525^7=568^7

 

⑥还有，如

90^8十223^8十478^8十524^8十748^8十1088^8十1190^8十1324^8=1409^8

 

总之，现在只完成了勾股定理和费马大定理的证明，以及由反例得到的特例，其他问题都未有定论，对它们理论的证明几乎是不可能。就费马猜想的证明，几乎用了近四个100年。

为了读者进一步理解，我再次介绍它的证明思路。

 

费马猜想的命题:设x，y，z，为整数，整数m>2，求证:

方程x^m+y^m=z^m……(1)

没有正整数解。

 

简练明晰的费马猜想，要知道的是，有没有三个整数满足方程(1)？难就难在，当m充分大时，人工和计算机都无法找到两个正整数的m次方之和等于一个正整数的m次方？

 

1，不必考虑负整数的问题。因为，当m为偶数时，若x为负整数，不改变方程(1)，正象(±3)^2+(±4)^2=(±5)^2。当m为奇数时，若x为负整数，方程(1)通过移项又变成原有形式:y^m=z^m+(-x)^m。称(1)式为丢番图方程，并约定未知数两两互质，若不然，约去公约数后又把方程化为了原有形式。

 

2，解决费马猜想，就是找到满足方程(1)的可能的解，再证明这个解不存在。

 

3，设z=n(正整数)，方程(1)为

x^m+y^m=n^m……(2)

方程(2)明确了在集合M:{1，2^m，3^m，…，(n-1)^m，n^m}中，寻找两个数之和等于n^m。

对于模n，考查M中余数，①集合M为模n的完全剩余系:{0，1，2，…，n-1}；②集合M不是模n的完全剩余系。

当M为模n的完全剩余系时，若方程(2)有解，必有

r^m+(n-r)^m=n^m…(3)

显然，方程(3)是不成立的，因为r+(n-r)=n，左端小于右端。依据是:若x+y=z，那么x^m+y^m<(x+y)^m=z^m。

当M不是模n的完全剩余系时，若方程(2)有解，必有两正整数r与d，使r^m和d^m关于模n同余，满足:

d^m+(n-r)^m=n^m…(4)

于是，费马猜想就转化为方程(4)除n=r=d外无整数解了。

方程(4)应该存在一个美妙的证法。

4，设m为素数(m>2，只要证明m为素数时方程(1)无解，那么，就可以证明m为合数时方程(1)也无解，当m=2^t，t>1整数的情况，另外需要证明m=4时方程(1)无解本文不再证明)，方程(4)变形为:

d^m=n^m-(n-r)^m……(5)

由(5)，容易导出r整除d^m，即r|d^m。所以，方程(5)有正整数解的必要条件是，r^m与d^m关于模n同余(换句话说，r^m与d^m被n除的余数相等)，且r|d^m，这还没完，还会导出方程(5)有整数解的其他约束条件。

直观地看看m=3，5，7时情况。

①d^3=n^3-(n-r)^3

=3n^2xr-3nr^2+r^3

d^3-r^3=3nr(n-r)。

②d^5=n^5-(n-r)^5

=5n^4r-10n^3r^2+10n^2r^3-5nr^4+r^5

d^5-r^5=5n^3r(n-2r)+5nr^3(2n-r)

=5nr[n^2(n-2r)+r^2(2n-r)]

=5nr(n^3-2n^2r+2r^2n-r^3)

=5nr[(n-r)(n^2+nr+r^2)-2nr(n-r)]

=5nr(n-r)(n^2-nr+r^2)。

 

③d^7=n^7-(n-r)^7

=7n^6r-21n^5r^2+35n^4r^3-35n^3r^4+21n^2r^5-7nr^6

=7nr(n^5-3n^4r十5n^3r^2-5n^2r^3+3nr^4-r^5)

=7nr[(n^5-r^5)-3nr(n^2-r^2)+5n^2r^2(n-r)]

=7nr(n-r)K，其中，K=n^4+n^3r+n^2r^2+nr^3+r^4

-3n^2r-3nr^2+5n^2r^2)。

一般地，方程(5)化简有

d^m-r^m=mnr(n-r)K，…(6)

其中，k=n^(m-3)+nrc+r^(m-3)，c∈正整数。所以，方程(5)有解必要条件有:

mnr(n-r)丨d^m-r^m。…(7)

5，只要能证明(7)不成立，就证明了费马猜想，多么美妙！是否存在简单明确的方法判断出(7)不成立？专业的读者一定得到了启示，产生了思路，请给出你的美妙方法，完美回答这个世界之问吧。

二年前我发现的这种证明，已经是一个幸运了，它可能不是最筒洁的证法或许有漏洞，我把这个证明冷落了好久了，今天才来自查证明的叙述方式和逻辑性，现在更加明晰了只要判明r|d^m-r^m不成立，就证明了(7)式不成立。

先做两组数据，从数据中理解证明中的逻辑性。

①模10对{1，2^3，3^3，4^3，5^3，6^3，7^3，8^3，9^3，10^3}的剩余系为全完剩余系{1，8，7，4，5，6，3，2，9，0}。

②模18对{1，2^3，3^3，…，18^3}的剩余系为:

{1，8，9，10，17，0，1，8，9，10，17，0，1，8，9，10，17，0}。不是完全剩余系。

6，由(7)式知，r|d^m。设r≠1，①r|d；②r|d^m，但r不整除d。

①当r|d时，由(6)式知，必导出r|n，与d，n-r，n两两互质矛盾。

②当r不整除d时，对r进行质因数幂分解(如，18=2x3^2)，总有一个质因数幂的指数大于1，所以，不妨设r=a^t，d=ab，其中a为质数，t为大于1的整数，b为正整数，且(a，b)=1。这样就满足了r|d^m，r不整除d。于是，由(6)式，得

 

b^m-a^(mt-m)=mna^(t-m)(n-r)k…(8)

 

当t>m时，将导致a|b^m，与(a，b)=1矛盾。

当t<m时，若a|n，与n-r，d，n两两互质矛盾；若a|m，m为质数，导致a=m，r=m^(m-1)，(8)式化为:

b^m-m^[m(m-2)]=n(n-r)k…(9)

其中，r=m^(m-1)。

当t=m时，即r=a^m，d=ab，(8)式化为:

b^m-r^(m-1)=mn(n-r)k……(10)

其中，r=a^m，a为质数。

7，求b。

因为d^m=n^m-(n-r)^m

=r[n^(m-1)+n^(m-2)r+…+nr^(m-2)+r^(m-1)]

用n代替(n-r)，或用(n-r)代替n，得

rm(n-r)^(m-1)<d^m<rmn^(m-1)，…(11)

 

①当d=mb，r=m^(m-1)时，由(11)式得

(n-r)^(m-1)<b^m<n^(m-1)，

令n-r=p^m，p为正整数，得

[p^(m-1)]^m<b^m<n^(m-1)<[p^(m-1)+r]^m

开m次方，得

p^(m-1)<b<p^(m-1)+r

由(9)式的特解，得(9)式的一般解为:

b=p^(m-1)+m^(m-2)，

n=p^m+m^(m-1)。…(12)

但它不是方程(9)式的解。代入(9)式就会产生矛盾。具体过程如下:

b^m-m^[m(m-2)]=n(n-r)k，→

[p^(m-1)+m^(m-2)]^m-m^[m(m-2)]=mnp^mk

左端展开，并消去m^[m(m-2)]项，并提取p的公因数，得

p^(m-1)xg=mnp^mk，其中g为正整数，且(p，g)=1。

观察上式，p|g，矛盾。

②当d=ab，r=a^m时，由(10)式有特解b=a^(m-1)，n=a^m，

于是，由(10)式，得一般解为:

b=mp^(m-1)+a^(m-1)，

n=mp^m+a^m。……(13)

但它不是方程(10)式的解。代入(10)式就会产生矛盾。具体过程与①类似。

b^m-r^(m-1)=mn(n-r)k，→

[mp^(m-1)+a^(m-1)]^m-r^(m-1)=m^2np^mK，

左端消去r^(m-1)项，并提取p的公因数，得

p^(m-1)xg=m^2np^mK，(p，g)=1。

导致p|g，矛盾。

先前我给出的《费马猜想的证明(李扩继)》在这部分的推导比较复杂，没有现在的简洁。

证明了r≠1时，等式(4)不成立，只要再证明r=1时等式(4)不成立，就完成了费马猜想的证明，即

d^m+(n-1)^m=n^m…(14)

除n=d=1外，无整数解。

而(14)式不成立与r≠1的证明是类似的。

由(11)式，r=1，d=b，得

mp^(m-1)<d<mp^(m-1)+1

由p为整数，所以，d为正整数不存在。

至此，费马猜想得证。

总之，证明费马猜想的方法就是，假定x^m+y^m=z^m有正整数解成立，z=n(正整数)，这样必存在两个正整数d，r(0<r<d)，满足d^m，r^m对于模n同余，使等式d^m+(n-r)^m=n^m成立。由此导出等式成立的必要条件:

mrn|d^m-r^m。判断这个整除问题，从r入手，考查r存在的各种情况，再证明这情况都不成立，从而证明了费马猜想。

费马猜想这个会下金蛋的母鸡，近四个世纪以来，推动了数论的发展，在这里，虽然得到了它的一个证明，但对它的研究不会结束，它依然在推动着数论的发展。(李扩继)