C++实现计算组合数（附带源码）

最新推荐文章于 2025-03-20 22:21:31 发布

Katie。

最新推荐文章于 2025-03-20 22:21:31 发布

阅读量1k

点赞数 12

分类专栏： c、c++实战项目文章标签： c++ 开发语言

本文链接：https://blog.csdn.net/m0_61840987/article/details/145346390

版权

c、c++实战项目专栏收录该内容

516 篇文章

订阅专栏

1. 项目背景

组合数是组合数学中的一个重要概念，表示从 n 个不同元素中选取 k 个元素的方案数，记作 C(n,k) 或。组合数的计算在概率论、统计学、计算机科学等领域有广泛应用。

计算组合数的方法有多种，包括直接使用公式、递归方法、动态规划等。本项目将使用C++实现组合数的计算，并对比不同方法的效率和适用场景。

2. 项目需求

本项目的主要需求是编写一个C++程序，能够计算从 n 个元素中选取 k 个元素的组合数 C(n,k)。具体要求如下：

输入：用户输入两个整数 n 和 k。
输出：计算并输出组合数 C(n,k)。
功能：
- 支持多种计算方法（公式法、递归法、动态规划法）。
- 处理输入合法性（如 k≤n 且 k≥0）。
性能优化：
- 避免重复计算。
- 处理大数问题（如使用高精度计算）。

3. 项目实现思路

3.1 组合数公式

组合数的计算公式为：

其中 n! 表示 n 的阶乘。

3.2 递归方法

组合数满足递推关系：

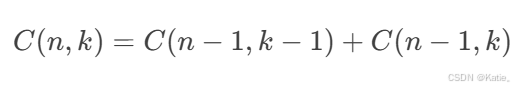
可以利用递归方法计算组合数，但需要注意重复计算问题。

3.3 动态规划方法

通过动态规划方法可以避免递归中的重复计算。使用二维数组存储中间结果，逐步计算组合数。

3.4 大数处理

对于较大的 n 和 k，组合数可能超出普通整数类型的范围。可以使用高精度计算库（如Boost.Multiprecision）或自定义大数类来处理。

4. 项目实现代码

#include <iostream>
#include <vector>
#include <stdexcept>

// 方法1：公式法计算组合数
unsigned long long combinationFormula(int n, int k) {
    if (k > n || k < 0) {
        throw std::invalid_argument("Invalid arguments: k must be between 0 and n.");
    }
    if (k == 0 || k == n) {
        return 1;
    }
    if (k > n - k) {
        k = n - k; // 利用组合数的对称性减少计算量
    }

    unsigned long long result = 1;
    for (int i = 1; i <= k; ++i) {
        result *= (n - k + i);
        result /= i;
    }
    return result;
}

// 方法2：递归法计算组合数
unsigned long long combinationRecursive(int n, int k) {
    if (k > n || k < 0) {
        throw std::invalid_argument("Invalid arguments: k must be between 0 and n.");
    }
    if (k == 0 || k == n) {
        return 1;
    }
    return combinationRecursive(n - 1, k - 1) + combinationRecursive(n - 1, k);
}

// 方法3：动态规划法计算组合数
unsigned long long combinationDP(int n, int k) {
    if (k > n || k < 0) {
        throw std::invalid_argument("Invalid arguments: k must be between 0 and n.");
    }

    std::vector<std::vector<unsigned long long>> dp(n + 1, std::vector<unsigned long long>(k + 1, 0));

    for (int i = 0; i <= n; ++i) {
        for (int j = 0; j <= std::min(i, k); ++j) {
            if (j == 0 || j == i) {
                dp[i][j] = 1;
            } else {
                dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
            }
        }
    }
    return dp[n][k];
}

int main() {
    int n, k;

    // 获取用户输入
    std::cout << "请输入n和k（用空格分隔）: ";
    std::cin >> n >> k;

    try {
        // 使用公式法计算
        std::cout << "公式法计算 C(" << n << ", " << k << ") = " << combinationFormula(n, k) << std::endl;

        // 使用递归法计算
        std::cout << "递归法计算 C(" << n << ", " << k << ") = " << combinationRecursive(n, k) << std::endl;

        // 使用动态规划法计算
        std::cout << "动态规划法计算 C(" << n << ", " << k << ") = " << combinationDP(n, k) << std::endl;
    } catch (const std::invalid_argument& e) {
        std::cerr << "错误: " << e.what() << std::endl;
    }

    return 0;
}