文献翻译链接:【空间-光谱重构网络:高光谱和多光谱图像融合】-CSDN博客
用于高光谱和多光谱图像融合的空间-光谱重构网络
目录
CMMI -cross mode message lnserting
Abstract
动机:重建HR-HSi(高分辨率-高光谱)时难以实现空间模式和光谱模式的跨(交叉)模式信息融合。
贡献:基于卷积神经网络,提出一种可解释的光谱重建网络,SSR-NET,有效将HSI与MSI融合。
是一种物理straightforward模型:
1)跨模式消息插入CMMI:产生初步融合的hr-hsi 保留LRHIS HRMSI最有价值的信息
2)空间网络重构:集中于空间边缘丢失指导下重建的LRHSI丢失的空间信息
3)光谱网络重构:空间边缘损失的约束下重建HRMSI丢失的光谱信息
对六种HSI数据进行对比实验,与七种先进方法进行比较
Instruction
低分辨率的高光谱图像与高分辨率的多光谱图像融合
传统方法:基于矩阵分解、基于贝叶斯、基于张量的方法 ,在光谱和空间之间有效传递信息有挑战性,对提高融合质量很重要
深度学习方法:强大的特征提取能力,基于cnn提出光谱重建网络
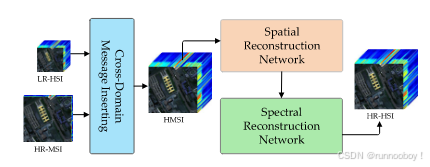
侧重于以高效和可解释方式跨空间和光谱模式传递有价值信息,三级网络
主要贡献:
1)基于CNN,本文首次提出了一种新的SSR-NET,用于更高效的HSI和MSI融合。 2)所提出的SSR-NET是一种物理straightforward的CNN模型,其在空间边缘损失Lspat和频谱边缘损失Lspec的约束下。Lspat和Lspec是专为空间和光谱重建而设计的。
3)与七种最先进的方法相比,所提出的SSR-NET在城市、帕维亚大学(PU)、帕维亚中心(PC)、博茨瓦纳和印第安松(IP)的五个HSI数据集上取得了最佳结果,在华盛顿特区购物中心(WDCM)的数据集上也取得了竞争性结果。这些实验结果证明了所提出的SSR-NET在LR-HSI和HR-MSI融合中的有效性和优越性。
spat用于重建空间信息,spec用于重建光谱信息
Related work
高光谱与多光谱融合
1.传统方法
1)基于矩阵分解:
2)贝叶斯
3)张量因式分解
2.深度学习
3D-cnn、深度hsi锐化、双分支
METHODOLOGY

CMMI -cross mode message lnserting
跨模式消息插入模块
是一种在多模态图像处理或多源数据融合任务中使用的技术。它通常指的是将一种数据模态中的信息或“消息”插入到另一种数据模态中,目的是提升模型的性能或利用两种模态互补的信息。
CMMI 允许将 HR-MSI(Y) 中的高分辨率空间信息插入到 LR-HSI(X) 中,在重建过程中提高空间细节的重建效果,同时保持 LR-HSI 中的完整光谱信息。
Reference HR-HSI (R) 参考
R∈R^(H×W×L )代表高分辨率的超光谱图像(HR-HSI),其中 H 和 W 分别是图像的高度和宽度,L是光谱波段的数量。是实际的、真实的高分辨率超光谱图像,它提供了一个标准或目标,用来衡量模型输出的质量。。
Estimated HR-HSI (Z) 估计
Z∈R^(H×W×L ) 代表经过模型处理后的估计高分辨率超光谱图像(HR-HSI)。是通过模型从低分辨率数据中估计出来的图像,目标是尽可能与 R 接近。
LR-HSI(X)
X∈R^(h×w×L) 是低分辨率的超光谱图像(LR-HSI),其中 h<H 和 w<W,表示它在空间分辨率上低于HR-HSI。 是通过对HR-HSI Z进行空间下采样获得的,通常采用双线性插值的方法进行下采样,采样比率为 r。
HR-MSI(Y):
Y∈R^(H×W×l 是高分辨率的多光谱图像(HR-MSI),其中 l 表示多光谱图像的波段数。是从HR-HSI Z 中按一定的波段间隔进行采样得到的,这些波段的索引集合为 {s1,s2,…,sl}{s_1, s_2, \dots, s_l}{s1,s2,…,sl},其中每个 sk代表第 k个波段。

输入的低分辨率超光谱图像 X是通过对高分辨率超光谱图像 Z 进行空间下采样得到的,且在下采样前,通常会对 Z 进行高斯滤波处理以模拟模糊效果。
高分辨率多光谱图像 Y 是通过从高分辨率超光谱图像 Z中选择特定的光谱波段进行采样得到的。选择的波段是按一定间隔的规律采样,因此 Y 的波段数 l少于HR-HSI的波段数 L。
<!--X 和 Y 在这里的角色是模拟数据。它们并不代表实际从传感器或实验中获得的数据,而是从估计的高分辨率超光谱图像(Z)中人为构造出来的-->
目标是从低分辨率的超光谱图像 X 和高分辨率的多光谱图像 Y 生成高分辨率的超光谱图像 Zpre ∈ R^(H×W ×L),利用了HR-MSI的空间信息和LR-HSI的光谱信息保持其相对的空间-光谱位置。
之后对X在进行空间上采样,采样到和HRMSI在空间上一样大,之后直接将HRMSI和LRHSI进行初步融合,

为了在空间和光谱模式之间初步传递信息,在HMSI中应用了一个卷积层,其核大小设置为3×3,空间高度和宽度步长设置为1。它被表示为

(提升空间细节:可以通过将来自多光谱图像的高分辨率空间信息插入到超光谱图像中,帮助改进空间细节的重建。
更好的光谱一致性:通过利用来自超光谱图像的光谱信息,可以丰富重建图像的光谱内容,同时保持较高的空间分辨率。
模态间协同:模型能够利用光谱和空间信息的互补性,从而生成更准确、更自然的重建图像。)
SpatRN空间边缘损失重建
为了从Zpre重建空间信息,另一个高度/宽度步长设置为1的3×3卷积层用作SpatRN,其公式为

在训练阶段使用跳跃连接操作来提高模型的稳定性.
为使SpatRN专注于基于空间边缘的空间信息的恢复,提出一种新的空间边缘损失来约束spatrn的输出

SpecRN光谱边缘损失重建
在空间重构之后,使用与SpatRN具有相同架构的充当SpecRN的又一个卷积层来进一步基于Zspat重构光谱信息
![]()
为了使SpecRN重视频谱恢复,本文还提出了频谱边缘损失(Lspec)来约束SpecRN的输出。Lspec的计算公式为

空间光谱边缘图
在CMMI、SpatRN和SpecRN之后,Zspec被用作最终估计的HR-HSI,表示为Zfus
![]()
对于Zfus,其通过表示为Lspec的融合损耗来优化,其公式为

在所提出的SSR-NET中,表示为L的总损耗是Lspat、Lspec和Lfus的总和
![]()
SSR-NET变体
为了探索SSR-NET的组件(包括CMMI、SpatRN和SpecRN)的有效性,设计了Spat-CNN、Spec-CNN、SpatR-NET、SpecRNET和SSR-NET的五种变体模型用于消融实验。
EXPERIMENTS
数据集:本文采用六个数据集来验证,包括Urban、PU、PC、博茨瓦纳、IP和华盛顿特区购物中心(WDCM)
这里采用的都是验证数据,全都是高分辨率高光谱图像,分为训练集和测试集。
评价指标:
RMSE均方根误差:它可用于测量R和Z之间的差异,小
PSNR峰值信噪比:以频带为单位评估重建的HR-HSI的空间质量。大
ERGAS[41]是专门为评估高分辨率合成图像的质量而设计的,它测量了估计的HRHSI的全局统计质量。 【参考文献 小
光谱角成像仪(SAM):SAM[42]通常用于评估每个像素的光谱信息保存程度 小
消融实验:
参考文献
SSF-CNN: Spatial and spectral fusion with CNN for hyperspectral image super-resolution
Multispectral and hyperspectral image fusion by MS/HS fusion net
HAMMFN: Hyperspectral and multispectral image multiscale fusion network with RAP loss
Remote sensing image fusion based on two-stream fusion network
知识补充
双线性插值
双线性插值(Bilinear Interpolation) 是一种常用的图像插值方法,用于在已知图像数据点之间估算未知数据点的值,尤其常用于图像缩放、旋转或变形等操作中。它在空间图像处理中非常常见,尤其是在进行图像的缩放时。
双线性插值的原理:
双线性插值是对图像中一个像素点的值进行插值估算的方法。假设需要插值的点位于已知四个像素点的矩形区域内,双线性插值通过对这四个已知点的值进行加权平均来计算插值点的值。
具体步骤如下:
-
确定四个已知点: 假设我们需要估算的点 ( P(x, y) ) 位于四个已知点的周围,这四个已知点的坐标为:
-
( P_1(x_1, y_1) )
-
( P_2(x_2, y_1) )
-
( P_3(x_1, y_2) )
-
( P_4(x_2, y_2) )
这些已知点的位置形成一个矩形网格。
-
-
按 x 方向插值: 首先,在横坐标 ( x ) 方向进行插值。我们对 ( P_1 ) 和 ( P_2 ) 进行插值,得到 ( P_1(x) ): [ P_1(x) = P_1 \times \frac{x_2 - x}{x_2 - x_1} + P_2 \times \frac{x - x_1}{x_2 - x_1} ]
同样地,对 ( P_3 ) 和 ( P_4 ) 进行插值,得到 ( P_2(x) ): [ P_2(x) = P_3 \times \frac{x_2 - x}{x_2 - x_1} + P_4 \times \frac{x - x_1}{x_2 - x_1} ]
-
按 y 方向插值: 接下来,在纵坐标 ( y ) 方向对 ( P_1(x) ) 和 ( P_2(x) ) 进行插值,得到最终的插值结果 ( P(x, y) ): [ P(x, y) = P_1(x) \times \frac{y_2 - y}{y_2 - y_1} + P_2(x) \times \frac{y - y_1}{y_2 - y_1} ]
公式总结:
假设 ( (x, y) ) 是需要插值的位置,四个已知点 ( P_1, P_2, P_3, P_4 ) 的坐标为 ( (x_1, y_1), (x_2, y_1), (x_1, y_2), (x_2, y_2) ),那么双线性插值的公式为: [ P(x, y) = P_1 \cdot \frac{x_2 - x}{x_2 - x_1} \cdot \frac{y_2 - y}{y_2 - y_1} + P_2 \cdot \frac{x - x_1}{x_2 - x_1} \cdot \frac{y_2 - y}{y_2 - y_1} + P_3 \cdot \frac{x_2 - x}{x_2 - x_1} \cdot \frac{y - y_1}{y_2 - y_1} + P_4 \cdot \frac{x - x_1}{x_2 - x_1} \cdot \frac{y - y_1}{y_2 - y_1} ]
双线性插值的特点:
-
平滑性:由于双线性插值使用的是周围四个点的加权平均,插值结果相对平滑,不会产生显著的锯齿状边缘。
-
计算简单:相对于其他高阶插值方法(如三次插值),双线性插值计算较为简单且快速。
-
应用广泛:在图像处理、计算机视觉和图像变换(如图像缩放、旋转)中,双线性插值常常被用来填充图像中的缺失像素或对图像进行缩放。
示例:
假设我们有一个低分辨率的图像,想要通过双线性插值将其缩放到更高的分辨率。对于每个新的像素位置,通过上述的双线性插值方法计算新像素的值,以填补新图像中的所有像素点。
总之,双线性插值是一种通过考虑目标点周围四个已知点的加权平均来估算新像素值的方法,它在图像缩放、变换等处理中广泛应用,能够提供较为平滑和自然的插值效果。
下采样
在 SSR-NET 框架中,X 是 低分辨率超光谱图像(LR-HSI),而 Z 是 估计的高分辨率超光谱图像(HR-HSI)。至于 X 为什么是通过 Z 下采样得到的,下面是一个解释:
1. 下采样过程的作用
在图像重建和超分辨率任务中,通常会通过对高分辨率图像进行下采样来生成低分辨率图像。这个过程模拟了真实世界中的低分辨率图像数据获取情况,例如,传感器或采集设备的限制导致获得的图像分辨率较低。
在 SSR-NET 中,X 作为低分辨率超光谱图像(LR-HSI),是通过对 Z(高分辨率超光谱图像)进行下采样得到的。具体来说,这个下采样过程通常包含以下步骤:
-
Z 是目标图像(真实的高分辨率超光谱图像),通过对 Z 进行空间下采样来生成低分辨率图像 X。
-
下采样过程中,图像的分辨率降低,像素数量减少,图像的细节和空间分辨率也会有所丢失。
2. 下采样的动机
下采样的动机在于通过 X 模拟低分辨率的输入数据,以便训练网络去重建高分辨率图像。通过这样做,网络会学习从 低分辨率的超光谱图像(X) 中恢复出 高分辨率超光谱图像(Z) 的方法。
具体的步骤可能如下:
-
Z 是目标图像,它包含完整的空间和光谱信息。
-
通过对 Z 进行下采样,得到 X,其中图像的空间分辨率被降低,光谱信息可能也受到了一定程度的丢失。
-
通过使用 X 和高分辨率的多光谱图像(HR-MSI,Y)作为输入,网络学习如何将低分辨率的超光谱图像 X 重建为高分辨率超光谱图像 Z。
3. 下采样和高分辨率图像重建
下采样的作用不仅仅是生成低分辨率图像 X,它也模拟了实际应用中可能遇到的情况。例如,传感器限制可能使得我们只能获取低分辨率的超光谱图像,而目标是通过重建算法恢复出原始的高分辨率超光谱图像。
在这个过程中,网络的目标是尽量从低分辨率图像 X 中恢复出高分辨率图像 Z,因此网络会学习到如何有效地结合来自低分辨率图像和高分辨率多光谱图像的信息,从而生成一个清晰、准确的高分辨率超光谱图像。
4. 为什么使用下采样后的X
-
训练数据的模拟:在现实中,我们往往只有低分辨率的图像数据(X),而高分辨率的图像数据(Z)是目标。因此,网络需要通过低分辨率图像(X)来学习如何生成高分辨率图像(Z)。
-
下采样模型的逼近:通过从 Z 进行下采样生成 X,可以更好地模拟真实世界中采集低分辨率图像的过程,让网络在训练时获得与实际应用更加接近的数据结构和任务目标。
5. 总结
X 是通过对 Z(高分辨率超光谱图像)进行下采样得到的低分辨率图像,这个过程在 SSR-NET 中起到了模拟现实应用中的低分辨率图像输入的作用。网络的目标是通过学习如何从低分辨率图像(X)和高分辨率多光谱图像(Y)中恢复出高分辨率的超光谱图像(Z)。
上采样
上采样(Upsampling) 是一种图像处理技术,主要用于 增加图像的分辨率,即将图像的空间尺寸(高度和宽度)扩大。在图像处理和计算机视觉中,上采样通常用于将低分辨率图像转换为高分辨率图像。
上采样的基本概念:
-
上采样的目标:提高图像的分辨率,使得每个像素之间的间隔变小,从而让图像变得更加细腻和清晰。
-
操作方式:上采样会将原本的图像插值(或扩展)到一个更大的尺寸,通常是将每个像素值扩展到多个新像素中,产生更高的空间分辨率。
上采样的常见方法:
-
最近邻插值(Nearest Neighbor Interpolation):
-
这种方法通过复制最近的像素值来填充新生成的像素。它简单但可能导致图像出现块状的效果,尤其是在放大较大的图像时。
-
-
双线性插值(Bilinear Interpolation):
-
双线性插值通过计算周围四个像素的加权平均值来插入新的像素,使得图像的过渡更加平滑。它通常比最近邻插值产生更自然的效果。
-
-
立方插值(Cubic Interpolation):
-
立方插值使用周围16个像素的加权平均进行插值,比双线性插值效果更好,但计算开销较大。它通常用于高质量的图像重建。
-
-
转置卷积(Transposed Convolution 或 Deconvolution):
-
转置卷积是深度学习中常用的一种上采样方法,通常用于卷积神经网络(CNN)中,通过学习的卷积核来进行上采样,并生成更加细致的图像。它也常用于生成对抗网络(GANs)和自编码器(Autoencoders)等模型中。
-
上采样的作用:
-
图像增强:上采样可以帮助恢复图像的细节,使得图像看起来更清晰,适用于需要高分辨率图像的应用。
-
图像重建:在超分辨率重建任务中,目标是从低分辨率图像生成高分辨率图像。通过上采样,可以将低分辨率图像的空间分辨率提高,然后通过更复杂的模型来恢复更多的细节。
-
深度学习中的应用:在卷积神经网络(CNN)和生成对抗网络(GAN)等深度学习模型中,上采样通常用于恢复或生成更高分辨率的图像。
举例:
假设有一张 2×2 的低分辨率图像:
[ \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix} ]
通过上采样(例如使用双线性插值),我们将其转换成 4×4 的图像。在插值过程中,新的像素值会基于原始像素值和邻近像素的加权平均值生成,结果会是:
[ \begin{bmatrix} 1 & 1.5 & 1.5 & 2 \ 2 & 2.5 & 2.5 & 3 \ 3 & 3.5 & 3.5 & 4 \ 3 & 4 & 4 & 4 \end{bmatrix} ]
可以看到,图像的尺寸从 2×2 扩大到了 4×4,并且像素之间的过渡变得更加平滑。
总结:
上采样就是通过某种插值方法将图像的空间分辨率提升,使图像的尺寸变大,并且尽可能保留原图的信息或者生成更加细腻的细节。在深度学习和图像处理应用中,上采样常常被用于图像重建、增强和生成任务。
ReLU
ReLU(Rectified Linear Unit)是一种在深度学习中广泛使用的激活函数,用于神经网络中的各个层,尤其是在卷积神经网络(CNN)和全连接网络中。
ReLU的定义:
ReLU 是一个简单的非线性函数,其数学表达式为:
[ \text{ReLU}(x) = \max(0, x) ]
这意味着对于输入 x:
-
如果 x > 0,则输出 x。
-
如果 x ≤ 0,则输出 0。
因此,ReLU 函数的输出是一个线性的非负值,任何负数输入都会被截断为 0,而正数则保持不变。
主要特点:
-
非线性:尽管 ReLU 看起来像是分段线性函数,但它是非线性的,可以帮助神经网络捕捉复杂的模式。
-
计算效率高:ReLU 函数非常简单,计算成本低。与其他激活函数(如 Sigmoid 和 Tanh)相比,它不涉及指数运算,因此计算效率较高。
-
稀疏激活:ReLU 的一个特点是会将输入中的负值压缩为 0,这导致了网络中大部分神经元在给定输入时被“关闭”或“稀疏激活”。这种稀疏激活有助于提高神经网络的训练效率。
ReLU的优缺点:
优点:
-
避免梯度消失问题:与 Sigmoid 和 Tanh 激活函数不同,ReLU 不会出现梯度消失问题。Sigmoid 和 Tanh 在输入值较大或较小时会导致梯度变得非常小,从而使得反向传播的过程变得困难,而 ReLU 的梯度在正区间是常数 1,能够避免这一问题。
-
计算简单高效:ReLU 只需要对输入值进行简单的判断和输出,不需要复杂的计算,计算速度非常快,适合大规模神经网络训练。
-
加速收敛:由于其简单性和不容易遇到梯度消失问题,使用 ReLU 的网络通常比使用 Sigmoid 或 Tanh 激活函数的网络收敛速度要快。
缺点:
-
“死亡 ReLU”问题:如果在训练过程中,某些神经元的输入始终为负值,那么这些神经元的输出将一直是 0,导致它们在反向传播过程中无法更新,从而“死掉”——即这些神经元不再参与模型学习。这种现象被称为 "dying ReLU" 问题。
-
这个问题可以通过使用 Leaky ReLU 或 Parametric ReLU(PReLU)等变种来缓解。
-
-
不对称:ReLU 在负值区域为 0,导致其输出对负值不敏感,这使得它在某些情况下表现不如其他激活函数。
ReLU的变种:
为了克服 ReLU 的一些缺点(如“死亡 ReLU”问题),出现了多个变种,常见的有:
-
Leaky ReLU:
-
公式:( \text{Leaky ReLU}(x) = \max(\alpha x, x) )
-
其中,( \alpha ) 是一个很小的常数(例如 0.01)。
-
这种变种允许在负值区域有一个小的斜率,避免了神经元完全“死亡”的问题。
-
-
Parametric ReLU (PReLU):
-
公式:( \text{PReLU}(x) = \max(\alpha x, x) )
-
与 Leaky ReLU 类似,但不同之处在于,( \alpha ) 不再是固定的常数,而是通过训练学习得到的。
-
-
ELU (Exponential Linear Unit):
-
ELU 是 ReLU 的进一步改进,允许在负区域有一个平滑的指数输出,以减少梯度消失问题,并加速训练。
-
总结:
-
ReLU 是一种简单而高效的激活函数,广泛应用于深度神经网络中,尤其是在卷积神经网络(CNN)中。
-
它可以加速网络的训练过程,并减少梯度消失问题,但也可能导致一些神经元“死亡”的问题。为了解决这个问题,使用 Leaky ReLU 或 PReLU 等变种是常见的做法。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








