【文献阅读笔记】Multispectral and Hyperspectral Image Fusion by MS/HS Fusion Net

爱喝两碗汤

已于 2024-11-12 15:22:38 修改

阅读量1.1k

点赞数 26

分类专栏：多源遥感图像融合文章标签：笔记深度学习图像处理

于 2024-11-11 22:44:12 首次发布

本文链接：https://blog.csdn.net/m0_62111862/article/details/143697305

版权

多源遥感图像融合专栏收录该内容

12 篇文章

订阅专栏

MHFnet：Multispectral and Hyperspectral Image Fusion by MS/HS Fusion Net

abstract

高光谱成像，通常只能以视频速率捕获高分辨率多光谱（HrMS）和低分辨率高光谱（LrHS）图

我们提出了一种基于模型的深度学习方法，用于合并 HrMS 和 LrHS 图像以生成高分辨率高光谱（HrHS）图像，我们设计了一种迭代算法，通过利用近端梯度法来求解该模型。构建了一个深度网络，称为 MS/HS 融合网络，通过卷积神经网络学习近端算子和模型参数

instruction

常规观测模型

Y:HRMSI Z:LRHSI X:HRHSI

R: 光谱响应 C:线性算子卷积算子和下采样矩阵D

问题：缺乏针对MS/HS融合的专门设计、忽视观测模型和操作符R、C、忽视高光谱图像的普遍先验结构（光谱低秩性）

贡献：

1）提出了一个新的MS/HS融合模型，考虑了观测模型（1）和（2），并利用高光谱图像（HrHS）在光谱维度上的低秩性先验结构，以减少光谱失真。利用近端梯度法设计一个迭代算法求解模型

2）迭代算法展开成一个深度网络架构，称为MS/HS Fusion Net (MHFnet)，该网络能够隐式地学习待估计的矩阵Yˆ。获得(\hat{Y})之后，我们可以轻松地用(Y)和(\hat{Y})得到X。在训练过程中，网络可以端到端自动学习模型中的所有参数，无需像传统方法那样事先估计空间和光谱响应（R和C）

3）将该方法与现有的最新算法进行了比较，并通过一系列合成数据和真实问题的实验结果，展示了该方法在定量和视觉效果上的优越性。

基于深度学习的方法只是使用当前深度学习工具包中一些现成的组件组装网络，并非专门针对所研究的问题设计。因此，这种技术的主要缺点是对这个特定的MS/HS融合任务缺乏可解释性。具体而言，这种“黑箱”深度模型忽略了HS图像的内在观测模型（1）、（2）以及明显的先验结构，如光谱相关性。

MS/HS融合模型

模型公式化

目标函数：

MS/HS融合网络

每个阶段将 HrMS 图像、LrHS 图像以及前一阶段的输出作为输入，并输出一个更新的作为下一层的输入

公式解读：

x3表示沿通道模式进行张量乘法计算，在tensorflow中使用二维卷积实现，

C表示空间下采样算子，分解为二维卷积和下采样算子，downsample θ一串表示二维通道卷积和平均池化算子组成的下采样网络，θ(k)表示第k个阶段要用到的滤波器，

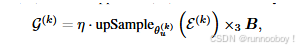
C^T表示空间上采样算子，通过二维转置卷积实现

prox 待确定的近端算子，采用resnet来学习，proxnet是一个resnet

Y G输入残差网络，用resnet来学习近端算子，输出计算好的y^k+1

迭代算法对应的网络设计

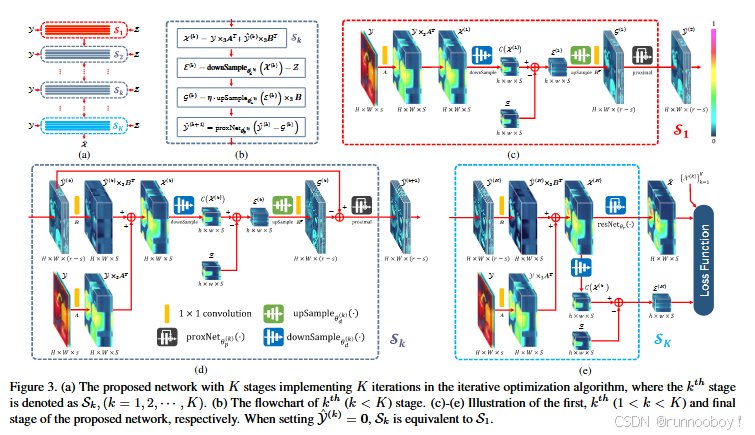
在这里插入图片描述

图a：所提出的具有K个阶段的网络在迭代优化算法中实现了K次迭代，其中第K个阶段表示为Sk，（K=1，2，··，K）。

图b：第k（k<k）阶段的流程图。

图c-e：分别说明拟议网络的第一阶段、第k阶段（1<k<k）和最后阶段。当设置Yˆ（k）=0时，Sk等于S1

第一步：k=1时y^1=0,

最后一步：X(k)内在编码了低秩结构，实际中HRMSI会受到轻微噪声干扰，低秩假设与实际存在差距，则X(k)不完全等同于待估计的值，在最终阶段添加了一个resnet

这样，网络能够更好地从低秩假设的结果中修正和恢复出真实的高分辨率高光谱图像

最后一步为什么要用resnet？

在最后一步使用 残差网络（ResNet） 的主要目的是进一步缩小当前估计与真实高分辨率高光谱（HrHS）图像之间的误差，并且进行更细致的调整，最终生成更准确的 HrHS 图像。以下是具体原因：

1. 降低近似误差：

在前面的迭代过程中，模型通过低秩假设和近端梯度更新方法逐步逼近真实的 HrHS 图像，但这些假设和更新方法并不能完全表示真实数据的复杂性，特别是在真实应用场景中，高光谱图像可能包含更多复杂结构和细节。因此，最后一步使用残差网络，利用其强大的特征学习和逼近能力，可以进一步修正由于模型假设简化带来的误差。

2. 补偿低秩假设的局限性：

在模型设计中，采用了低秩结构来进行高光谱图像的逼近，这种假设尽管有效，但在实际数据中可能并不完全成立。低秩假设通常会导致一定的精度损失，特别是在光谱或空间信息丰富的图像中。使用 ResNet 能帮助模型在最后一步对低秩假设的不足进行补偿，从而使最终输出更符合真实 HrHS 图像的复杂性。

3. 增强非线性表达能力：

残差网络具有很强的非线性特征表达能力，可以捕捉到图像中更细微的纹理、结构信息。通过引入 ResNet 进行最终的校正，能够在逼近解的基础上，捕捉到更复杂的图像细节信息，使得输出的 HrHS 图像更加自然、清晰。

4. 保持计算稳定性：

残差网络具有稳健的训练特性，特别适合在深层网络中校正误差。它能避免梯度消失问题，从而保证了在最后一步校正的有效性，增强了网络的稳定性，使得最终输出的结果更为精确。

总结

使用 ResNet 作为最后一步，能在初步得到的近似解上进行微调，提高最终输出图像的质量。这一步既可以弥补模型中假设的局限性，也可以提升图像的细节表现力，使得输出的 HrHS 图像更加接近真实数据。

θ表示网络中的所有参数

网络训练

损失训练：

第一项：损失函数的主要部分，确保模型输出的估计值尽可能靠近真实值

第二项：每个阶段与真实值的差距，有助于找到每个阶段的正确参数

第三项：观测模型2的残差

训练数据：

当HRHSI不可用时如何处理？

整个流程的目的是在没有 HrHS 图像的情况下，通过对现有数据进行处理来生成训练数据，用于训练模型。

原始数据（Original data）
- 流程从原始数据开始，这些原始数据可能包括高分辨率多光谱（HrMS）图像和低分辨率高光谱（LrHS）图像。
原始样本（Original sample）
- 从原始数据中提取原始样本。这些样本可能是从原始图像中裁剪或选择出来的特定区域。

3.下采样过程：中间的流程展示了两次下采样操作。

第一次下采样：原始样本经过第一次下采样操作后，生成了训练样本（Training sample）。这一步骤的目的是为了创建能够用于训练模型的数据。训练样本会进一步被处理成训练数据（Training data），这个过程可能涉及到一些数据整理和组织的操作，使得数据能够被模型有效地学习。
第二次下采样：原始样本经过另一次下采样操作后，生成了输入样本（Input samples）。这里的输入样本包括了 Y 和 Z，Y 和 Z 可能分别代表高分辨率多光谱（HrMS）图像和低分辨率高光谱（LrHS）图像相关的数据。这表明下采样操作不仅仅用于生成训练数据，还用于生成模型训练过程中的输入数据。

不太懂：HRHSI不是不可用吗怎么能对他降采样呢

我们在空间上对HrMS图像和LrHS图像进行降采样，以便原始LrHS图像可以作为降采样数据的参考。？？？？

实现细节：

我们使用TensorFlow框架实现和训练我们的网络。我们使用Adam优化器对网络进行50000次迭代训练，批量大小为10，学习率为0.0001。参数的初始化和其他实施细节在补充材料中列出。

experiments

CAVE数据集

评价措施：采用五个定量图像质量指标（PQI）进行性能评估，包括峰值信噪比（PSNR）、光谱角映射器（SAM）[49]、相对全局维度分解（ERGAS[38]）、结构相似性（SSIM[39]）、特征相似性（FSIM[51]）。SAM计算所有空间位置上目标MSI和参考MSI的光谱矢量之间的平均角度，ERGAS根据每个频带中MSE的加权和测量恢复图像的保真度。PSNR、SSIM和FSIM是传统的PQI。他们根据MSE表1评估目标图像和参考图像之间的相似性结构一致性、感知一致性。ERGAS和SAM越小，PSNR、SSIM和FSIM越大，融合结果越好。

模型验证：

为了验证所提出的MHF网络的效率，我们首先在CAVE多光谱图像数据库上比较了具有不同设置的MHF网的性能[46]8。该数据库由32个场景组成，空间大小为512×512，包括以10nm步长从400nm到700nm的全光谱分辨率反射率数据（共31个波段）。我们通过整合所有具有相同模拟光谱响应R的地面真值HrHS带来生成HrMS图像（RGB图像），并通过对32×32像素块进行平均，以32的因子对地面真值进行降采样来生成LrHS图像，如[2,16]。

为了准备训练样本，我们从CAVE数据库中随机选择20幅HS图像，并从中提取96×96个重叠的补丁作为训练的参考HrHS图像。然后，所使用的HrHS、HrMS和LrHS图像的大小分别为96×96×31、96×96 x 3和3×3×31。数据库的其余12幅HS图像用于验证，其中原始图像被视为地面真值HrHS图像，HrMS和LrHS图像的生成与训练样本类似。

模拟数据实验

然后，我们在模拟数据上评估MHF网络，并与最先进的方法进行比较。

比较方法包括：FUSE[41]9、ICCV15[18]10、GLP-HS[31]11、SFIMHS[19]11、GSA[1]11、CNMF[48]12、M-FUSE[40]13和SASFM[14]14，代表了最先进的传统方法；PNN[30]和3D-CNN[28]代表了最先进的基于DL的方法。我们还将提出的MHF网络与实现的ResNet方法进行了比较。

真实数据实验

实验中使用由World View - 2（WV - 2）获取的罗马斗兽场的样本图像

conclusion

在本文中，我们提供了一种新的MS/HS融合网络。该网络利用了深度学习的优势，即所有参数都可以从训练数据中学习，而对数据的先验假设较少，并且进一步考虑了MS/HS融合数据背后的生成机制。这是通过基于观测模型构建新的MS/HS融合模型，并将算法展开为受优化启发的深度网络来实现的。因此，该网络对任务具有特定的可解释性，并且可以帮助以纯粹的端到端方式发现空间和光谱响应算子。在模拟和真实MS/HS融合案例上的实验证实了所提出的MHF - net相对于现有最佳方法的优越性。

知识补充

观测模型

是一种用于描述系统状态与观测结果之间关系的数学模型。

不适定逆问题

“ill-posed inverse”即“不适定逆问题”。

在数学和科学计算中，一个问题如果满足解存在、解唯一以及解连续依赖于数据这三个条件，就被称为适定问题；反之，如果不满足这些条件中的一个或多个，就称为不适定问题。对于不适定逆问题，通常解可能不存在、不唯一或者对数据的微小变化非常敏感。例如，在图像重建、反问题求解（如从测量的电磁场数据反推物体的形状等）中经常会遇到不适定逆问题。为了解决不适定逆问题，通常需要采用正则化方法等技术来稳定求解过程，获得相对合理的解。

先验假设：假设图像X可以通过少数几个基元素（例如字典元素或特征）表示，这样就能在数学上通过优化方法将图像恢复成一个稀疏的表示。比如高分辨率图像X的空间信息可能是稀疏的，可以通过字典学习或字典匹配来表示。

通俗解释：基于已有的经验或对问题的理解，假设某些特性或规律在数据中是存在的。这些假设为我们提供了一些额外的信息或约束，帮助我们从有限的观测数据中推断出更合理的结论

平滑性假设：假设图像X的变化是平滑的，像素之间的变化不会太剧烈。这在很多实际问题中成立，比如自然图像通常是连续的，邻近像素的值不会有太大差异。

低秩假设：如果X是一个矩阵（例如多光谱或高光谱图像），可以假设X具有低秩，即其矩阵的秩较小，可以通过低秩矩阵恢复技术来解决。

光谱满秩

这句话的意思是，HrMS 图像（高分辨率多光谱图像）的波段数通常不多，例如，常见的 RGB 图像 只有 3 个波段。在这种情况下，HrMS 图像 的光谱信息通常是“满秩的”（full rank）。这里的“满秩”指的是矩阵的秩等于它的最小维度，也就是说，图像的光谱信息没有冗余或过度依赖。

具体解释：

波段数：
- 高分辨率多光谱图像（HrMS）是由多个光谱波段组成的，每个波段对应图像在不同光谱范围（如红、绿、蓝，简称RGB，或其他更多的波段）的信息。
- 例如，RGB图像通常包含三个波段：红色（R）、绿色（G）和蓝色（B）。这三个波段用于描述图像中的颜色信息。
满秩的含义：
- 在数学中，矩阵的秩是衡量矩阵中独立信息量的指标。如果一个矩阵的秩等于它的最小维度（行数和列数中的较小者），则称这个矩阵是“满秩的”。
- 对于一个光谱图像矩阵来说，如果它是满秩的，意味着图像的所有波段所包含的信息是线性独立的，没有冗余的光谱信息。例如，RGB图像的三个波段（红色、绿色、蓝色）通常是独立的，每个波段都提供不同的颜色信息。
光谱模式上的满秩性：
- 在高分辨率多光谱图像中，光谱模式指的是图像在每个像素处的多个波段的信息。如果HrMS图像的波段数较少（例如只有3个），那么这些波段通常可以用线性独立的方式表示图像的光谱信息，即这些波段之间没有过多的冗余。这样的图像矩阵就被称为“光谱上满秩”。
- 例如，RGB图像中的红、绿、蓝三种颜色信号是独立的，因此它的光谱矩阵通常是满秩的。

为什么重要：

如果一个图像的光谱矩阵是满秩的，这意味着该图像的光谱信息是“完全的”，每个波段都提供了不同的、不可替代的信息。这对于图像处理算法（如图像融合、恢复等）来说非常重要，因为它可以利用每个波段的独特信息，而不必担心光谱信息中的冗余。
另一方面，如果波段之间有较高的相关性（例如过多的冗余），那么该图像的光谱矩阵可能不是满秩的，这就意味着某些波段可以通过其他波段的线性组合来表示，从而减少了可用的信息量。

因此，在这段话中，提到 HrMS 图像 在波段数较少时通常是满秩的，意味着这些图像的光谱信息在空间上是独立的，没有过多冗余，便于进一步处理。

低秩假设

在该模型中，低秩假设主要体现在 HrHS 图像 X 的表示方法上，以及模型设计和推导过程中对 HrHS 图像的特征假设。这种假设使得模型能够更有效地进行数据压缩和逼近，同时减少计算复杂度。

HrHS 图像的表示形式：在模型设计中，HrHS 图像 XXX 被表示为：

X=YA+Y^B+NxX = Y A + \hat{Y} B + N_xX=YA+Y^B+Nx

其中：

Y是已知的 HrMS 图像（通常为满秩），
Y^\hat{Y}Y^ 是未知的低秩成分，
A和 B为系数矩阵，用于表示 HrHS 图像的不同成分。

这个分解方式基于低秩假设：即通过较少的低秩成分Y^ 和系数矩阵 A、B，就能够很好地逼近真实的 HrHS 图像 XXX。这种假设在很大程度上减少了模型参数和数据复杂度。

近端梯度更新过程：在近端梯度更新公式中，模型使用了低秩成分 Y^ 的更新，而不是直接更新 X。这一步的设计也是基于低秩假设，认为通过低秩成分的更新能够捕捉到 HrHS 图像的大部分特征，并在后续阶段进一步调整。

低秩假设的推导依据：根据假设，HrHS 图像的谱信息往往是低秩的，因为它们在高光谱成像中表现出较强的相关性。例如，在高光谱图像中，不同波段的像素值之间存在较高的相关性。因此，模型可以将 HrHS 图像在低维空间中近似表示，并通过少量成分实现逼近。

使用矩阵分解来逼近 HrHS：在建模过程中使用了矩阵分解，例如在公式：

Y≈XR

中，通过将 HrHS 图像 X 与系数 R 的乘积来表示 HrMS 图像 Y。这种方法在推导中利用了低秩分解的思想，即认为 HrHS 图像 X 可以在更低秩的成分上逼近，从而降低计算复杂性。

低秩假设的原因

在高光谱成像中，不同波段的图像数据往往有较强的相关性，即它们的谱信息通常可以被压缩成低秩表示，这样模型可以更高效地学习和表示图像结构。这种低秩假设帮助模型在保留关键信息的同时减少了参数数量，使得训练过程更快且更稳定

低秩假设的作用

这种低秩假设的使用可以有效减少模型的自由度，使得模型能够在不完全依赖全部高维数据的情况下，逼近和重建 HrHS 图像，从而提升效率和收敛速度。此外，低秩假设还能减少噪声的影响，提升图像的复原质量。

目标函数详细解释

近端梯度算法

是一种常用于解决带有正则化项的优化问题的迭代算法，特别是在优化问题中涉及到非光滑（non-smooth）函数时

张量

张量（Tensor）是数学和计算机科学中用来表示多维数据的一个重要概念，它是对向量和矩阵的推广。在简单的情况下，张量可以被视为一个多维数组，但它的定义更加广泛和抽象。张量广泛应用于物理学、计算机科学（尤其是在深度学习中）、工程学等领域。

张量的基本概念：

标量（Scalar）：
- 0维张量：一个单一的数值，表示的是一个常数。例如，5 或 3.14 都是标量。
向量（Vector）：
- 1维张量：一组有序的数字，可以理解为一维数组或列表。例如，[ 1, 2, 3 ] 就是一个向量，它有三个元素。
矩阵（Matrix）：
- 2维张量：一个二维数组，由行和列组成。例如，以下是一个 ( 2 \times 3 ) 的矩阵： [ \begin{bmatrix} 1 & 2 & 3 \ 4 & 5 & 6 \end{bmatrix} ] 矩阵通常表示数据的二维结构，比如图像中的像素信息。
高维张量（Higher-order Tensor）：
- 3维及以上的张量：当数据有更多的维度时，它就不再是普通的标量、向量或矩阵。它是一个包含多个维度的数据结构。例如，一个 3维张量可以表示为一个立方体，其中每个元素可以通过三个索引来表示：例如 ( T(i,j,k) )，其中 (i)、(j)、(k) 是张量的三个维度的坐标。

张量的表示：

标量：( a \in \mathbb{R} )（一个数值）。
向量：( \mathbf{v} \in \mathbb{R}^n )（一个一维数组，有n个元素）。
矩阵：( M \in \mathbb{R}^{m \times n} )（一个二维数组，有m行n列）。
高维张量：( T \in \mathbb{R}^{m \times n \times p} )（一个三维数组）。

张量的维度（Order）：

张量的维度（有时也称为阶数或阶数）表示了它有多少个坐标轴。
- 标量：维度为 0。
- 向量：维度为 1。
- 矩阵：维度为 2。
- 高维张量：维度大于2。

例如：

一个三维张量可以表示为 ( T(i, j, k) )，其中 (i)、(j) 和 (k) 是该张量的三个维度。
一个四维张量可以表示为 ( T(i, j, k, l) )，依此类推。

张量在深度学习中的应用：

在深度学习中，张量通常是用于表示和处理数据的基本单位。特别是在框架如 TensorFlow 和 PyTorch 中，张量是用来表示图像、音频、文本等多维数据的基础结构。以下是一些应用示例：

图像数据：一张彩色图像通常表示为一个三维张量，其中两个维度表示图像的空间维度（高度和宽度），第三个维度表示颜色通道（例如RGB的三个通道）。
- 例如，一个 ( 256 \times 256 ) 的 RGB 图像会表示为一个 ( 256 \times 256 \times 3 ) 的张量。
视频数据：视频是一系列连续的图像，通常表示为一个四维张量，维度分别对应：时间、宽度、高度和颜色通道。例如，一个 10 帧的视频，每帧大小为 ( 256 \times 256 )，则可以表示为一个 ( 10 \times 256 \times 256 \times 3 ) 的张量。
深度学习中的批处理：在深度学习中，我们常常同时处理多个样本（例如，在训练时处理多个图像）。这些图像通常被组织成一个批量（batch），并表示为一个四维张量，维度分别是批次大小、图像的高度、宽度和颜色通道。

张量运算：

张量也支持各种数学运算，包括加法、乘法、转置、求逆等。常见的张量运算包括：

点积（Dot product）和矩阵乘法：用于计算张量之间的关系。
元素级运算（Element-wise operations）：对张量中的每个元素应用相同的操作。
张量重塑（Reshaping）：改变张量的形状（例如，转置矩阵或将二维矩阵展平成一维向量）。
卷积操作（在卷积神经网络中常用）：通过滑动窗口的方式在张量上应用卷积操作。

张量与矩阵的关系：

矩阵是张量的一种特殊情况，它是二维的张量。张量可以有更多的维度，但矩阵仅限于二维。
张量包含了向量、矩阵和更高维数据的所有结构，具有更强大的表示能力。

总结：

张量是一个多维的数据结构，可以表示标量、向量、矩阵或更高维的数据。
张量在深度学习和许多数学领域中扮演着重要角色，是处理和表示数据的基础。

tensorflow

resnet

损失训练

在本文中，损失训练（loss training）指的是通过定义一个损失函数（loss function），并利用训练数据来优化网络参数，以最小化损失函数值的过程。这一过程在基于深度学习的MS/HS融合网络（MHFnet）中起着关键作用，用于指导网络学习如何从高分辨率多光谱（HrMS）图像(Y)和低分辨率高光谱（LrHS）图像(Z)中准确地恢复出目标高分辨率高光谱（HrHS）图像(X)。 ### 损失函数的定义 1. 如文中所述，训练损失函数定义为：(L=|\hat{\mathcal{X}}-\mathcal{X}|F^2+\alpha\sum{k = 1}^K|\mathcal{X}^{(k)}-\mathcal{X}|F^2+\beta|\mathcal{E}^{(K)}|F^2)。 - 第一项(|\hat{\mathcal{X}}-\mathcal{X}|F^2)是所提出网络的最终输出(\hat{\mathcal{X}})与真实值(\mathcal{X})之间的像素级(L_2)距离（Frobenius范数的平方）。这是损失函数的主要组成部分，直接衡量了网络最终生成的图像与真实目标图像之间的差异程度。例如，如果该项的值越小，说明网络输出的图像在像素级别上越接近真实的(X)，也就意味着网络在恢复(X)方面的准确性越高。 - 第二项(\alpha\sum{k = 1}^K|\mathcal{X}^{(k)}-\mathcal{X}|F^2)是每个阶段输出(\mathcal{X}^{(k)})与真实值(\mathcal{X})之间的像素级(L_2)距离之和（乘以权重(\alpha)）。该项有助于在网络的每个阶段找到正确的参数，因为合适的参数设置会使得每个阶段的输出(\mathcal{X}^{(k)})更接近真实的(\mathcal{X})。通过在训练过程中考虑每个阶段的误差，能够使网络在学习过程中更加稳定和准确地逼近最终目标，避免在最后阶段才发现错误而难以调整。 - 第三项(\beta|\mathcal{E}^{(K)}|F^2)是网络最后阶段观测模型（2）的残差的像素级(L_2)距离（乘以权重(\beta)）。它从观测模型的角度提供了额外的约束，确保网络生成的结果在满足观测模型的条件下尽可能准确。 ### 训练过程 1. 网络使用Adam优化器对损失函数(L)进行优化，训练过程包含多个迭代步骤。在每次迭代中，根据当前的网络参数计算损失函数的值，然后通过反向传播算法计算损失函数对网络参数的梯度。Adam优化器根据这些梯度信息来更新网络参数，使得损失函数的值逐渐减小。 2. 例如，在计算梯度时，会涉及到网络中各个层的操作和参数，如在计算(\mathcal{X}^{(k)})、(\mathcal{E}^{(k)})、(\mathcal{G}^{(k)})等过程中所涉及的参数（如(A)、(B)、(\theta_d^{(k)})、(\theta_u^{(k)})、(\theta_p^{(k)})等）都会根据损失函数的梯度进行调整。通过不断重复这个过程，网络逐渐学习到如何从输入的(Y)和(Z)中生成最接近真实(X)的图像，从而提高网络在MS/HS图像融合任务中的性能。 ### 作用和意义 1. 损失训练使得网络能够自动从训练数据中学习到有效的特征表示和参数设置，而不需要手动设计复杂的特征提取和融合规则。通过最小化损失函数，网络能够自适应地调整自身的结构和参数，以适应不同类型和特性的输入图像数据，从而提高了方法的通用性和适应性。 2. 与传统方法相比，这种基于损失训练的深度学习方法在处理MS/HS融合问题时，能够更好地捕捉图像中的复杂非线性关系，从而在恢复高分辨率高光谱图像方面取得更好的效果。通过在模拟和真实数据上的实验结果可以看出，经过损失训练后的MHFnet在各种评估指标（如峰值信噪比PSNR、光谱角映射器SAM等）上表现优异，证明了损失训练对于提高网络性能和图像融合质量的重要性。

模型参数总结

在这个网络中，包含的参数主要可以分为以下几类：

1. 网络参数 ( \Theta )

( \Theta ) 是网络的总参数集合，包含了网络中所有需要学习的参数。这些参数在训练过程中会通过优化算法自动调整，以最小化损失函数并提升网络的性能。
具体来说，( \Theta ) 包含了：
- 卷积核（Filters）：用于卷积操作的权重，尤其是用于残差网络（ResNet）中的卷积层。
- 全连接层的权重：如果网络中包含全连接层（Dense Layer），那么这些层的权重也包含在 ( \Theta ) 中。
- 偏置项（Bias）：网络中的各个层通常会有偏置参数，用于调整激活函数的输出。

2. 迭代过程中的参数

在每次迭代过程中，网络会处理估计图像的更新。具体来说，以下几个参数在每个阶段可能会进行更新：

( Y^{(k)} )：第 (k) 次迭代中的估计值，表示当前阶段的输出。
( Y^{(1)} = 0 )：第一阶段的初始化值。
( A ) 和 ( B )：在优化过程中，矩阵 ( A ) 和 ( B ) 是与张量 ( Y ) 和 ( \hat{Y} ) 相关的参数，它们在通过优化模型（如近端梯度算法）时会被调整。这些矩阵用于低秩表示，并与张量乘法配合使用。
( R )：是一个矩阵，用于将最终的输出 ( X^{(K)} ) 映射到多光谱图像 ( Y ) 上。在定理 1 中，( R ) 是需要通过训练或优化来确定的。

3. 残差网络中的参数（ResNet 参数）

残差网络（ResNet） 中的权重和偏置。残差网络通常由多个卷积层、激活函数、跳跃连接和批量归一化（batch normalization）层组成。因此，残差网络的参数包括：
- 卷积核：用于图像特征提取的卷积核权重。
- 偏置：每个卷积层的偏置参数。
- 批量归一化参数：包括缩放因子（gamma）和平移因子（beta）。
- 激活函数的参数：如 ReLU 激活函数中可能有一些与学习相关的参数。

4. 正则化项中的参数

( \lambda )：正则化参数，用于在优化过程中平衡损失函数的两个部分（即数据拟合项和正则化项）。( \lambda ) 控制着正则化对网络训练的影响程度。正则化项通常用于约束模型的复杂度，防止过拟合。
正则化函数 ( f(\hat{Y}) )：用于对估计值 ( \hat{Y} ) 进行正则化的函数。正则化函数的具体形式依赖于问题的需求，常见的有 L1 正则化、L2 正则化等。

5. 损失函数中的参数

损失函数一般由两个部分组成：数据拟合项和正则化项。数据拟合项是用来度量网络输出与真实值之间的差异，正则化项是用来约束网络的复杂度。

数据拟合项：通常是一个范数（如 Frobenius 范数），表示模型预测的图像 ( \hat{X} ) 与真实图像 ( Z ) 之间的差异。

例如，公式 (11) 中的目标项：

[ g(Y^{(k)}) = | C(Y A + Y^{(k)} B) - Z |_F^2 ]

这个范数中使用的 ( C ) 是一个操作符，它作用于 ( Y A + Y^{(k)} B )，并且需要优化的参数包括 ( A )、( B )、和 ( C ) 中的内容。

6. 网络的超参数

除了需要学习的参数外，网络还包括一些 超参数，这些超参数通常在训练之前手动设置，并且在训练过程中不会变化。包括：

学习率（Learning rate）：控制网络参数更新的速度。
批次大小（Batch size）：每次更新中使用的训练数据的数量。
迭代次数（Epochs）：训练过程中数据集的循环次数。

总结

网络的参数主要包括以下几个部分：

网络的训练参数 ( \Theta )：包括卷积层、全连接层的权重、偏置项等。
迭代中的参数：如 ( Y^{(k)} )、( A )、( B )、( R )，这些会在每个阶段通过优化调整。
残差网络的参数：卷积核、批量归一化参数等，用于修正最终的估计结果。
正则化参数 ( \lambda )：用于平衡损失函数中的数据拟合和正则化部分。
损失函数的相关参数：如 ( C ) 和 ( f(\hat{Y}) )，它们在训练中用于引导模型的优化。

这些参数会在端到端的训练过程中自动学习和优化，以实现最终高质量的多光谱和高分辨率高光谱图像融合。

卷积网络应用

是的，模型中确实有用到卷积神经网络（CNN）。具体来说，卷积神经网络在以下几个方面发挥了重要作用：

1. 残差网络（ResNet）

在最终阶段的网络结构中，为了减少由低秩假设带来的误差和噪声，网络中加入了 残差网络（ResNet）。残差网络本质上是一种 卷积神经网络，通过引入跳跃连接（skip connections）来缓解梯度消失问题，并加速训练。

卷积层：残差网络中的卷积层用于提取特征，帮助进一步修正和优化图像的估计。
跳跃连接：残差网络中的跳跃连接将输入直接加到输出中，从而减少网络中的信息丢失，并使网络能够更好地拟合复杂的映射关系。

2. 卷积操作用于张量乘法

在模型中提到的张量和矩阵乘法（如公式 (19) 中的 ( X^{(k)} = Y \times_3 A^T + \hat{Y}^{(k)} \times_3 B^T )）实际上也可以通过卷积操作来实现。具体来说，TensorFlow 等框架中，可以通过 1×1 卷积 来实现沿着通道（或光谱）维度的张量乘法。