分区四元数航天器姿态控制 & Matlab复现

在实际应用中，控制算法需要考虑各种工程约束，包括控制力矩受限，即不能逾越飞轮或喷气执行机构的最大控制力矩；角速度限制，以满足航天器平稳性需求、导航带宽需求以及角速率陀螺量程等要求；控制模式一体化要求, 尽可能将机动和跟踪两种模式用一个统一公式表达等等。

分区四元数姿态控制[1]的基本思想是把姿态分为内区和外区，设计角速度规划器，在外区以恒定的、满足约束的角速度使航天器姿态快速机动到内区；在内区通过PI控制使角速度随姿态线性变化，积分项还可以抵抗常值干扰力矩。此外，添加对力矩的饱和约束，满足控制力矩受限的工程约束。内区与外区结合，同时满足姿态机动和姿态稳定要求。下图为角速度规划器。

其详细控制模型和其他特点见论文[1]。

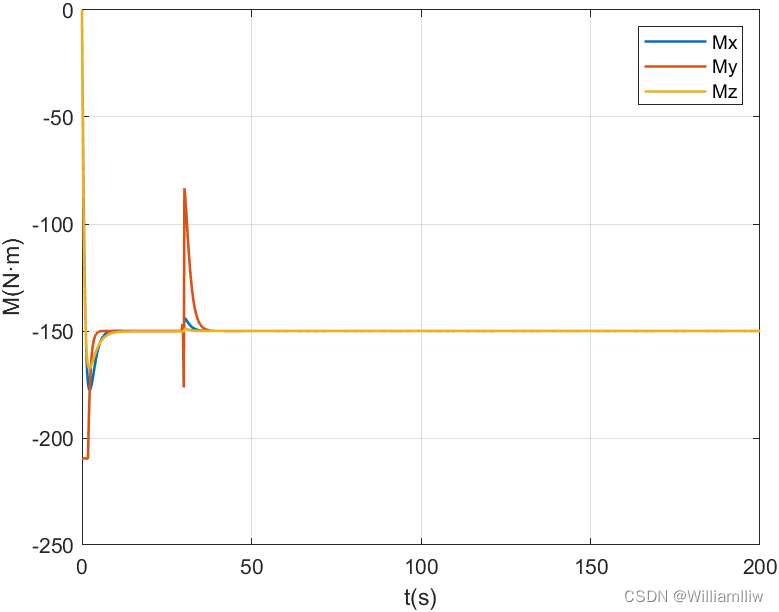
复现结果如下，4张图依次是q-w相平面轨迹、姿态四元数、角速度、控制力矩。

主函数如下：

% 分区四元数航天器姿态控制
clear; clc; close all;
%% 参数定义（国际单位）
global I qExp d
% 系统参数
I = diag([4012, 2807, 2334]); % 惯性矩阵
% 控制参数
global M1 M2 tauMax k1 k2 alpha0 wT sBar qTbar k
M1 = 0.07475; M2 = 0.06725; % 限幅参数
tauMax = 300; % 最大控制力矩
k1 = 2; k2 = 0.78; % 角速度跟踪律的PI系数，rad/s
alpha0 = [0, 0, 0];
wT = 3*pi/180; % 最大角速度幅值
sBar = (M1+M2)/k1; % 控制力切换误差, rad/s
qTbar = 0.0349; % 分区四元数边界值
k = wT/qTbar; % 1.5 rad/s
% 初始状态
situ = 1;
switch(situ)
    case 1
        w0 = [0; 0; 0]; % 角速度
        q0 = [0.707; 0; 0.707; 0]; % 姿态四元数
    case 2
         w0 = [0; 20; 0]*pi/180; % 角速度
         q0 = [0.707; 0; 0.707; 0]; % 姿态四元数
end
% 期望状态
% qExp = @(t) [cos(t/100*pi-pi/4); 0; sin(t/100*pi-pi/4); 0];
qExp = @(t) [1; 0; 0; 0];
% 干扰
d = [150; 150; 150];
% 仿真参数
tspan = [0 200];
% 参数检查
if ~(M1 > M2 && M2 > norm(I^(-1)*d, inf))
    warning('不满足定理1条件3');
end
if abs(sBar - (M1+M2)/k1) > 1e-6
    warning('不满足定理1条件4');
end
judge = norm(I, inf)*((2*M1/k1+wT)^2 + sqrt(3)/2*k*(2*M1/k1+wT) + M1);
if tauMax < judge*0.8
    warning('不满足定理1条件5');
end
%% 仿真
[t, y] = ode45(@dynamic, tspan, [q0', w0', alpha0]);
%% 绘图
% 计算力矩、期望角速度
n = length(t);
tau = zeros(3, n); wd = zeros(3, n);
qEr = zeros(4, n);
for ii = 1: n
    [tau(:, ii), wd(:, ii), qEr(:, ii)] = showDynamicPara(t(ii), y(ii, :));
end
figure(1);% 姿态时间曲线
% plot(t, y(:, 1), t, y(:, 2), t, y(:, 3), t, y(:, 4), 'linewidth', 1.25);
plot(t, qEr(1, :), t, qEr(2, :), t, qEr(3, :), t, qEr(4, :), 'linewidth', 1.25);
xlabel('t(s)'); ylabel('误差四元数'); grid on;
legend({'q0'; 'q1'; 'q2'; 'q3'});
figure(2);% 角速度时间曲线
plot(t, y(:, 5)*180/pi, t, y(:, 6)*180/pi, t, y(:, 7)*180/pi, 'linewidth', 1.25);
xlabel('t(s)'); ylabel('w(°/s)'); grid on;
legend({'wx'; 'wy'; 'wz'});
figure(3); % 期望角速度
wd = wd*180/pi;
plot(t, wd(1, :), t, wd(2, :), t, wd(3, :), 'linewidth', 1.25);
xlabel('t(s)'); ylabel('wd(°/s)'); grid on;
legend({'wdx'; 'wdy'; 'wdz'});
figure(4); % 力矩
plot(t, tau(1, :), t, tau(2, :), t, tau(3, :), 'linewidth', 1.25);
xlabel('t(s)'); ylabel('M(N·m)'); grid on;
legend({'Mx'; 'My'; 'Mz'});
figure(5); % 角速度对比
subplot(2, 2, 1);
plot(t, y(:, 5)*180/pi, t, wd(1, :), 'linewidth', 1.25);
xlabel('t(s)'); ylabel('wx(°/s)'); grid on;
legend({'wx'; 'wdx'});
subplot(2, 2, 2);
plot(t, y(:, 6)*180/pi, t, wd(2, :), 'linewidth', 1.25);
xlabel('t(s)'); ylabel('wy(°/s)'); grid on;
legend({'wy'; 'wdy'});
subplot(2, 2, 3);
plot(t, y(:, 7)*180/pi, t, wd(3, :), 'linewidth', 1.25);
xlabel('t(s)'); ylabel('wz(°/s)'); grid on;
legend({'wz'; 'wdz'});
figure(6); % 相平面轨迹
subplot(2, 2, 1);
plot(y(:, 2), y(:, 5)*180/pi, 'linewidth', 1.25);
xlabel('q1'); ylabel('wx(°/s)'); grid on;
subplot(2, 2, 2);
plot(y(:, 3), y(:, 6)*180/pi, 'linewidth', 1.25);
xlabel('q2'); ylabel('wy(°/s)'); grid on;
subplot(2, 2, 3);
plot(y(:, 4), y(:, 7)*180/pi, 'linewidth', 1.25);
xlabel('q3'); ylabel('wz(°/s)'); grid on;
subplot(2, 2, 4);
wn = sqrt((y(:, 5)).^2 + (y(:, 6)).^2 + (y(:, 7)).^2);
plot(2*acos(y(:, 1)), wn*180/pi, 'linewidth', 1.25);
xlabel('\theta(°)'); ylabel('wn(°/s)'); grid on;

动力学仿真函数：

function dx = dynamic(t, x)
%% 调试
if t > 50
    aa = 1;
end
%% 参数定义
q = x(1:4); % 姿态四元数
wb = x(5:7); % 角速度
dx = zeros(10, 1);
global I d qExp
%% 计算姿态误差
qD = qExp(t); % 当前时刻目标姿态
qDe = [qD(1); -qD(2); -qD(3); -qD(4)]; % 目标姿态四元数共轭
qE = quatMultiply(qDe, q);
%% 运动学
dx(1:4) = 0.5*quatMultiply(q, [0;wb]);
%% 控制律
[tau, wd, dAlpha] = partQuat(t, [qE; x(5:10)], dx(2:4));
dx(8:10) = dAlpha;
%% 动力学
dx(5:7) = I^(-1)*(tau + d - cross(wb, I*wb));
end

分区四元数控制子函数：

% 分区四元数控制律
function [tau, wd, dAlpha] = partQuat(t, x, dq)
%% 参数设定
% 控制参数
global M1 M2 tauMax k1 k2 wT sBar qTbar k
global I
% 状态量
q = x(1:4); % 姿态四元数
% 保证姿态控制方向的最小路径
if q(1) < 0
    q(2:4) = -q(2:4);
end
wb = x(5:7); % 角速度
alpha = x(8:10); % 积分器
dAlpha = zeros(3, 1);
%% 分区四元数控制
% 角速度规划器
if norm(q(2:4)) <= qTbar
    wd = -k*q(2:4); % 期望角速度
    dWd = -k*dq; % 期望角速度导数
else
    wd = -wT * q(2:4)/norm(q(2:4)); % 期望角速度
    % 期望角速度导数
    dWd = zeros(3, 1);
    qx = q(2); qy = q(3); qz = q(4);
    dWd(1) = ((qy^2+qz^2)*dq(1) - qx*(qy*dq(2) + qz*dq(3)))/(norm(q))^3;
    dWd(2) = ((qx^2+qz^2)*dq(2) - qy*(qz*dq(3) + qx*dq(1)))/(norm(q))^3;
    dWd(3) = ((qx^2+qy^2)*dq(3) - qz*(qx*dq(1) + qy*dq(2)))/(norm(q))^3;
end
% 误差角速度
s = wb - wd;
% 设置积分器饱和限制
for ii = 1:3
    if abs(abs(k2*alpha(ii)) - M2) < 1e-6 && alpha(ii)*s(ii) > 0
        dAlpha(ii) = 0;
    else
        dAlpha(ii) = s(ii);
    end
end
% 控制律
if norm(s, inf) <= sBar
    sigmaM1 = sat(-k1*s - k2*alpha, M1);
    tau = cross(wb, I*wb) + I*dWd + I*sigmaM1;
else
    tau = -tauMax * sign(s);
end
end
%% 矢量饱和函数
function out = sat(vec, M)
    n = length(vec);
    out = zeros(n, 1);
    for i = 1:n
        if abs(vec(i)) <= M
            out(i) = vec(i);
        elseif vec(i) > M
            out(i) = M;
        else
            out(i) = -M;
        end
    end
end

四元数乘法函数：

% 四元数圈乘计算P×Q
function out = quatMultiply(P, Q)
matQ = [Q(1), -Q(2), -Q(3), -Q(4);
        Q(2), Q(1), Q(4), -Q(3);
        Q(3), -Q(4), Q(1), Q(2);
        Q(4), Q(3), -Q(2), Q(1)];
out = matQ*P;
end

结果计算辅助函数

% 绘图用力矩、期望角速度
function [tau, wd, qE] = showDynamicPara(t, x)
%% 参数定义
q = x(1:4)'; % 姿态四元数
wb = x(5:7)'; % 角速度
%% 计算姿态误差
global qExp;
qD = qExp(t); % 当前时刻目标姿态
qDe = [qD(1); -qD(2); -qD(3); -qD(4)]; % 目标姿态四元数共轭
qE = quatMultiply(qDe, q);
%% 运动学
dx = 0.5*quatMultiply(q, [0;wb]);
%% 控制律
[tau, wd, ~] = partQuat(t, [qE; x(5:10)'], dx(2:4));
end

参考文献

[1]张洪华,关轶峰,胡锦昌,等.分区四元数姿态控制[J].自动化学报,2015,41(07):1341-1349.DOI:10.16383/j.aas.2015.c140624.