方格取数问题

更好的阅读体验 方格取数。

题目：方格取数

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

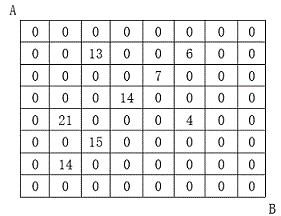
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 11 开始。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

N≤10

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

解题思路：

​ 从左上角走到右下角，于是想到DP中的数字三角形模型。关于数字三角形模型，可以去看这篇文章[线性DP](线性DP - 小樱桃 (oyto.github.io)/)。

​ 这题的不同点是，这里要取两次数，于是进行DP过程：

f[i1,j1,i2,j2]表示所有从(1,1),(1,1)分别走到(i1,j1),(i2,j2)路径的最大值。

如何处理“同一个格子不能被重复选择”？
    分析后发现，只有当i1 + j1 == i2 + j2时，两条路径的格子才可能重合，
    于是可以根据这条性质将思维优化成三维，

集合：f[k,i1,i2]表示所有从(1,1),(1,1)走到(i1,k-i1),(i2,k-i2)的路径的最大值
    k表示两条路线当前走到的格子的横纵坐标之和

属性：max

状态计算：
    以最后一步是从往下走还是往右走进行划分，因为有两次走法，所以被分成了四种情况
        下下、下右、右下、右右

​ 为什么下面四个状态转移方程能代表四种状态？

原因是，因为k 变小了1，先不看最后一步，如果i变小1，则j就不用变；如果i没有变，则j就需要变小1；
上述两种情况刚好对应了最后一步是向下、右走，的横纵坐标变化情况，又因为是两次一起走，故有四种情况。

x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);   //下 下
x = max(x, f[k - 1][i1 - 1][i2] + t);       //下 右
x = max(x, f[k - 1][i1][i2 - 1] + t);       //右 下

AC代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 15;

int n;
int f[N * 2][N][N], g[N][N];

int main()
{
    cin >> n;

    int a, b, c;
    while (cin >> a >> b >> c, a || b || c) g[a][b] = c;

    for (int k = 2; k <= n + n; k ++)   //枚举横纵坐标之和
        for (int i1 = 1; i1 <= n; i1 ++)    //枚举第一次走的横坐标
            for (int i2 = 1; i2 <= n; i2 ++)    //枚举第二次走的横坐标
            {
                int j1 = k - i1, j2 = k - i2;   //计算出两次走的纵坐标
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = g[i1][j1];  //如果两个坐标相等，只加一次，因为第二次走这里，已经被拿走清空了
                    if (i1 != i2) t += g[i2][j2];   //坐标不相同，就两个位置全加上
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);   //下 下
                    x = max(x, f[k - 1][i1 - 1][i2] + t);       //下 右
                    x = max(x, f[k - 1][i1][i2 - 1] + t);       //右 下
                    x = max(x, f[k - 1][i1][i2] + t);            //右 右
                }
            }

    printf("%d\n", f[n + n][n][n]);

    return 0;
}