点积(Dot product)
什么是点积
对两个向量执行点乘运算,也就是对两个向量的对应位相乘之后求和的操作,点积的结果为一个标量。
点积公式
设两个向量 a = [ a 1 , a 2 . . . a n ] a = [a_1,a_2...a_n] a=[a1,a2...an], b = [ b 1 , b 2 . . . b n ] b = [b_1,b_2...b_n] b=[b1,b2...bn],且a、b的行列数相同。
点积公式为: a ⋅ b = a 1 b 1 + a 2 b 2 + . . . + a n b n a \cdot b = a_1b_1+a_2b_2+...+a_nb_n a⋅b=a1b1+a2b2+...+anbn
几何意义
计算两向量夹角,或得到b向量在a向量方向上的投影。
公式: a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ a \cdot b = |a||b| \cos \theta a⋅b=∣a∣∣b∣cosθ
应用
可用于GJK算法中的支撑函数(参考GJK算法笔记)。给定一个向量和点集合,求方向上最远的一点。
结合 a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ a \cdot b = |a||b| \cos \theta a⋅b=∣a∣∣b∣cosθ,将点化成原点出发的向量,计算与向量d的点积(同时考虑了与向量d的夹角和距离)。
/// <summary>
/// 支撑点函数,获得给定方向上的最远点(支撑点)
/// 注意得到的是节点数组的索引
/// Get the supporting vertex index in the given direction.
/// </summary>
[MethodImpl(MethodImplOptions.AggressiveInlining)]
[Pure]
public int GetSupport(in Vector2 d)
{
var bestIndex = 0;
//把节点转换成从原点出发的向量
var bestValue = Vector2.Dot(Vertices[0], d);
for (int i = 1; i < Count; i++)
{
var value = Vector2.Dot(Vertices[i], d);
if (value > bestValue)
{
bestIndex = i;
bestValue = value;
}
}
return bestIndex;
}

也可以用来判断两个向量是否同一方向。
a ⋅ b > 0 a \cdot b > 0 a⋅b>0,同向
a ⋅ b = 0 a \cdot b = 0 a⋅b=0,垂直
a ⋅ b < 0 a \cdot b < 0 a⋅b<0,反向
进行长度比较时,为了避免平方根运算,可以使用点积。
Vector2.Dot(v,v)
Vector2.LengthSquared() //返回长度平方
叉积(Cross product)
向量a和向量b叉乘结果为一个向量,且这个向量垂直于ab构成的平面。
设向量a和b:
叉积公式:
其中i,j,k分别为x,y,z方向的单位向量。
也可表示为:
a x b = ∣ a ∣ ∣ b ∣ sin θ |a||b|\sin \theta ∣a∣∣b∣sinθ
应用
计算叉积
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static float Cross(in Vector2 a, in Vector2 b)
{
return a.X * b.Y - a.Y * b.X;
}
求垂直向量
public static Vector2 Cross(in Vector2 a, float s)
{
//对垂直向量进行缩放
return new Vector2(s * a.Y, -s * a.X);
}
a T a^{T} aT = Cross(a,1);
矩阵(Matrix)
逆矩阵
逆矩阵性质: A A − 1 = I AA^{-1} = I AA−1=I
逆矩阵求解公式:
[ a b c d ] − 1 = 1 a d − b c [ d − b − c a ] \begin{bmatrix} a & b \\ c & d \end{bmatrix} ^{-1} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} [acbd]−1=ad−bc1[d−c−ba]
其中行列式 d e t = 1 a d − b c det = \frac{1}{ad-bc} det=ad−bc1,如果行列式为0,则没有逆矩阵。这种矩阵为降秩矩阵,如下:
[ 3 4 6 8 ] − 1 = 1 3 × 8 − 4 × 6 [ 8 − 4 − 6 3 ] \begin{bmatrix} 3 & 4 \\ 6 & 8 \end{bmatrix} ^{-1} =\frac{1}{3\times8-4\times6} \begin{bmatrix} 8 & -4 \\ -6 & 3 \end{bmatrix} [3648]−1=3×8−4×61[8−6−43]
不满足 A A − 1 = I AA^{-1} = I AA−1=I,因而不存在逆矩阵。
线性方程组
设一个已知2x2矩阵A [ a 11 a 12 a 21 a 22 ] \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} [a11a21a12a22],已知向量b,未知向量x。求线性方程组解:
A ⋅ x = b A \cdot x = b A⋅x=b
可通过逆矩阵求解x:
x = A − 1 ⋅ b x = A^{-1} \cdot b x=A−1⋅b
根据逆矩阵求解公式:
A − 1 = 1 a 11 ⋅ a 22 − a 12 ⋅ a a 1 [ a 22 − a 12 − a 21 a 11 ] A_{-1} = \frac{1}{a_{11} \cdot a_{22} - a_{12} \cdot a_{a1}}\begin{bmatrix} a_{22} & -a_{12}\\ -a_{21} & a_{11} \end{bmatrix} A−1=a11⋅a22−a12⋅aa11[a22−a21−a12a11],
设 d e t = 1 a 11 ⋅ a 22 − a 12 ⋅ a a 1 det = \frac{1}{a_{11} \cdot a_{22} - a_{12} \cdot a_{a1}} det=a11⋅a22−a12⋅aa11
解向量x:
x . X = 1 d e t ⋅ ( a 22 ⋅ b . X − a 12 ⋅ b . Y ) x.X = \frac{1}{det} \cdot (a_{22} \cdot b.X -a_{12} \cdot b.Y) x.X=det1⋅(a22⋅b.X−a12⋅b.Y)
x . Y = 1 d e t ⋅ ( a 11 ⋅ b . Y − a 21 ⋅ b . X ) x.Y = \frac{1}{det} \cdot(a_{11} \cdot b.Y - a_{21} \cdot b.X) x.Y=det1⋅(a11⋅b.Y−a21⋅b.X)
矩阵实现
表示一个2x2的矩阵:
public struct Matrix2X2
{
public Vector2 Ex;
public Vector2 Ey;
public Matrix2X2(in Vector2 c1, in Vector2 c2)
{
Ex = c1;
Ey = c2;
}
public Matrix2X2(float a11, float a12, float a21, float a22)
{
Ex.X = a11;
Ex.Y = a21;
Ey.X = a12;
Ey.Y = a22;
}
public void Set(in Vector2 c1, in Vector2 c2)
{
Ex = c1;
Ey = c2;
}
/// <summary>
/// 1 0
/// 0 1
/// 将矩阵设置为一个单位矩阵
/// </summary>
public void SetIdentity()
{
Ex.X = 1.0f;
Ey.X = 0.0f;
Ex.Y = 0.0f;
Ey.Y = 1.0f;
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public void SetZero()
{
Ex.X = 0.0f;
Ey.X = 0.0f;
Ex.Y = 0.0f;
Ey.Y = 0.0f;
}
/// <summary>
/// 逆矩阵
/// </summary>
public Matrix2X2 GetInverse()
{
var a = Ex.X;
var b = Ey.X;
var c = Ex.Y;
var d = Ey.Y;
//行列式为0,则不存在逆矩阵
var det = a * d - b * c;
if (!det.Equals(0.0f))
{
det = 1.0f / det;
}
//逆矩阵求解公式:A^-1 = (1 / det) [d,-b,-c,a]
var matrix = new Matrix2X2();
matrix.Ex.X = det * d;
matrix.Ey.X = -det * b;
matrix.Ex.Y = -det * c;
matrix.Ey.Y = det * a;
return matrix;
}
/// <summary>
/// A * x = b求解向量x
/// </summary>
public Vector2 Solve(in Vector2 b)
{
var a11 = Ex.X;
var a12 = Ey.X;
var a21 = Ex.Y;
var a22 = Ey.Y;
var det = a11 * a22 - a12 * a21;
if (!det.Equals(0.0f))
{
det = 1.0f / det;
}
var x = new Vector2 { X = det * (a22 * b.X - a12 * b.Y), Y = det * (a11 * b.Y - a21 * b.X) };
return x;
}
//矩阵加运算
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Matrix2X2 operator +(in Matrix2X2 matrix1, in Matrix2X2 matrix2)
{
return new Matrix2X2(matrix1.Ex + matrix2.Ex, matrix1.Ey + matrix1.Ey);
}
}
旋转矩阵
可参考文章:
通过弧度制计算旋转矩阵,如下:
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}
[cosθsinθ−sinθcosθ]
向量和矩阵相乘可得到变换后的向量:
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
×
[
x
y
]
=
[
x
cos
θ
−
y
sin
θ
x
sin
θ
+
y
cos
θ
]
\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x\cos\theta - y\sin\theta \\ x\sin\theta + y\cos\theta \end{bmatrix}
[cosθsinθ−sinθcosθ]×[xy]=[xcosθ−ysinθxsinθ+ycosθ]
结合box2dSharp源码来看看:
Rotation结构体记录了刚体的旋转信息。
//| cosA -sinA |
//| sinA cosA |
public struct Rotation
{
public float Sin;
public float Cos;
public Rotation(float sin, float cos)
{
Sin = sin;
Cos = cos;
}
//弧度角获得正弦余弦
public Rotation(float angle)
{
//TODO_ERin optimize
Sin = (float)Math.Sin(angle);
Cos = (float)Math.Cos(angle);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public void Set(float angle)
{
//TODO_ERIN optimize
Sin = (float)Math.Sin(angle);
Cos = (float)Math.Cos(angle);
}
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public void SetIdentity()
{
Sin = 0.0f;
Cos = 1.0f;
}
}
Transform结构体记录刚体在b2World中的坐标和旋转信息。
public struct Transform : IFormattable
{
public Vector2 Position;
public Rotation Rotation;
public Transform(in Vector2 position, float angle)
{
Position = position;
Rotation = new Rotation(angle);
}
//Set this to the identity transform
public void SetIdentity()
{
Position = Vector2.Zero;
Rotation.SetIdentity();
}
public void Set(in Vector2 position, float angle)
{
Position = position;
Rotation.Set(angle);
}
}
将矩阵和向量相乘,如果是一个旋转矩阵,将向量从一个坐标系变换到另一个坐标系。
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector2 Mul(in Matrix2X2 m, in Vector2 v)
{
return new Vector2(m.Ex.X * v.X + m.Ey.X * v.Y, m.Ex.Y * v.X + m.Ey.Y * v.Y);
}
在二维空间中,如果两个旋转中心相同,两旋转矩阵相乘等效于旋转角度相加。
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Rotation Mul(in Rotation a, in Rotation b)
{
// | cosA -sinA | * | cosB -sinB | = | cosAcosB - sinAsinB -sinBCosA - sinAcosB |
// | sinA cosA | | sinB cosB | | sinAcosB + cosAsinB -sinBSinA + cosAcosB |
return new Rotation(a.Sin * b.Cos + a.Cos * b.Sin, a.Cos * b.Cos - a.Sin * b.Sin);
}
将向量还原为旋转前的向量,实际上就是把向量旋转相同角度但是方向相反。
假设旋转矩阵为 R ( θ ) = [ cos θ − sin θ sin θ cos θ ] R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} R(θ)=[cosθsinθ−sinθcosθ],则逆旋转矩阵为 R ( − θ ) = [ cos θ sin θ − sin θ cos θ ] R(-\theta) = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} R(−θ)=[cosθ−sinθsinθcosθ]。
代码如下:
//旋转向量
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector2 Mul(in Rotation q, in Vector2 v)
{
return new Vector2(q.Cos * v.X - q.Sin * v.Y, q.Sin * v.X + q.Cos * v.Y);
}
//还原为旋转前的向量
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector2 MulT(in Rotation a, in Vector2 v)
{
return new Vector2(a.Cos * v.X + a.Sin * v.Y, -a.Sin * v.X + a.Cos * v.Y);
}
/// <summary>
/// 先旋转向量再平移
/// </summary>
[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector2 Mul(in Transform T, in Vector2 v)
{
//计算相对T的位置
var x = T.Rotation.Cos * v.X - T.Rotation.Sin * v.Y;
var y = T.Rotation.Sin * v.X + T.Rotation.Cos * v.Y;
return new Vector2(x, y) + T.Position;
}
/// <summary>
/// 先平移再旋转向量
/// </summary>
public static Vector2 MulT(in Transform T, in Vector2 v)
{
//先移动再线性变换
var px = v.X - T.Position.X;
var py = v.Y - T.Position.Y;
return new Vector2(T.Rotation.Cos * px + T.Rotation.Sin * py, -T.Rotation.Sin * px + T.Rotation.Cos * py);
}
关于Mul()函数可以结合下面的例子理解:
如下图所示,设A点(2,2),B点在以A点为参考点的坐标系中坐标为(1,1)。
假设A为原点,则B可认为是B’逆时针旋转45度得到的。
B = [ 1 − 1 1 1 ] ⋅ [ 1 1 ] = [ 0 2 ] B= \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 1 \end{bmatrix} =\begin{bmatrix} 0 \\ 2 \end{bmatrix} B=[11−11]⋅[11]=[02]
则可得B的实际坐标为(0,2) + (2,2) = (2,4)









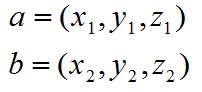
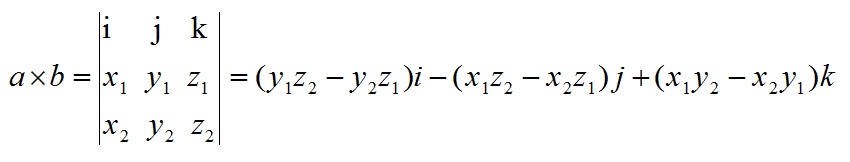














 771
771

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








